Неполные квадратные уравнения – это уравнения, которые не содержат всех членов, как полные квадратные уравнения. В данной статье мы рассмотрим шаги, необходимые для решения таких уравнений. Здесь вы найдете полезные советы и примеры для эффективного освоения методов решения неполных квадратных уравнений.
Связь между коэффициентами и корнями полного квадратного уравнения
При изучении полного квадратного уравнения, важно понять, как связаны его коэффициенты и корни. Знание этой связи поможет нам проанализировать уравнение и найти его корни.
Общая формула полного квадратного уравнения
Полное квадратное уравнение имеет следующий вид:
ax2 + bx + c = 0,

где коэффициенты a, b и c являются числами.
Соотношение между коэффициентами и корнями
Коэффициенты полного квадратного уравнения связаны с его корнями следующим образом:
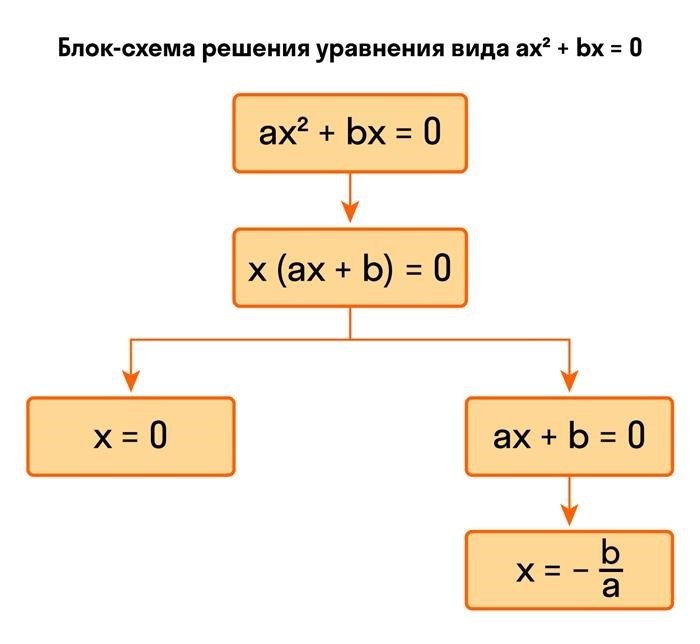
- Сумма корней равна отрицательному коэффициенту перед x с обратным знаком: x1 + x2 = -b/a.
- Произведение корней равно коэффициенту c/a.
Эти соотношения позволяют нам использовать коэффициенты уравнения для анализа и вычисления его корней.
Примеры
Рассмотрим несколько примеров, чтобы проиллюстрировать связь между коэффициентами и корнями полного квадратного уравнения:
| Полное квадратное уравнение | Сумма корней | Произведение корней |
|---|---|---|
| x2 – 5x + 6 = 0 | 5 | 6 |
| 2x2 + 3x – 2 = 0 | -3/2 | -1 |
| 3x2 + 2x + 1 = 0 | -2/3 | 1 |
Из этих примеров видно, как значения суммы и произведения корней связаны с коэффициентами уравнения. Это соотношение помогает нам анализировать и решать полное квадратное уравнение.
Таким образом, связь между коэффициентами и корнями полного квадратного уравнения играет важную роль в решении и анализе уравнений данного типа.

Что мы узнали?
Основные пункты, которые мы рассмотрели:
- Метод дополнения квадрата. Этот метод основан на приеме, заключающемся в добавлении и вычитании одного и того же числа для приведения уравнения к полному квадратному виду.
- Метод подстановки. Этот метод основан на замене переменной в уравнении и последующем решении полученного уравнения.
- Использование идентичностей. Идентичности в алгебре могут быть использованы для преобразования неполных квадратных уравнений в полные и более простые уравнения.
Используя эти методы, мы можем решать различные задачи и находить корни неполных квадратных уравнений. Также важно помнить о возможных ограничениях и условиях, которые могут появиться при решении таких уравнений.
Важный навык
Решение неполных квадратных уравнений требует хорошего понимания алгебраических методов и приемов. Это важный навык, который может быть применен в различных областях, включая математику, физику и экономику. Приобретение навыков решения неполных квадратных уравнений поможет нам в решении конкретных задач и развитии логического мышления.