Таблица sin cos tg ctg представляет собой набор значений синуса, косинуса, тангенса и котангенса для различных углов. Эта таблица широко используется в математике, физике и других науках, а также в инженерных расчетах и приложениях для вычислений. Она помогает определить значения этих тригонометрических функций для конкретного угла без необходимости проводить сложные математические вычисления. Таблица sin cos tg ctg удобна в использовании и предоставляет быстрый доступ к результатам.
Как пользоваться таблицей sin cos tg ctg
1. Определение функции
Перед использованием таблицы sin cos tg ctg необходимо определить, какую тригонометрическую функцию вы хотите вычислить. Возможные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).
2. Выбор угла
После определения функции нужно выбрать угол, для которого вы хотите вычислить значение функции. Угол может быть задан в градусах (°) или радианах (rad). Запишите значение угла, чтобы использовать его в таблице.
3. Поиск значения функции
Теперь, когда у вас есть функция и угол, можно приступать к поиску значения функции в таблице sin cos tg ctg. В таблице приведены значения функций для различных углов.
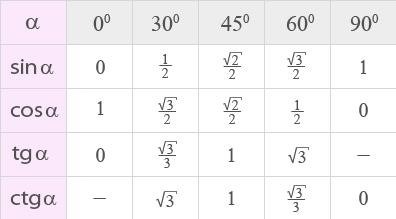
| Угол (°) | Угол (rad) | sin | cos | tg | ctg |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | — |
| 30 | π/6 | 1/2 | √3/2 | √3/3 | √3 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60 | π/3 | √3/2 | 1/2 | √3 | √3/3 |
| 90 | π/2 | 1 | 0 | — | 0 |
4. Интерполяция
Если требуется вычислить значение функции для угла, который не указан в таблице, можно использовать интерполяцию. Для этого нужно найти два ближайших угла в таблице и использовать их значения для расчета.
5. Проверка результата
После нахождения значения функции в таблице sin cos tg ctg рекомендуется проверить полученный результат при помощи калькулятора или специального программного обеспечения. Это поможет убедиться в точности вычислений и избежать ошибок.
Теперь вы знаете, как правильно пользоваться таблицей sin cos tg ctg. Используйте ее для удобных и точных вычислений значений тригонометрических функций.
Значения от 181 до 360 градусов
Значения синуса, косинуса, тангенса и котангенса неизменны при изменении градусов от 181 до 360. Давайте рассмотрим конкретные значения этих тригонометрических функций в данном диапазоне:
Таблица значений:
| Градусы | Синус | Косинус | Тангенс | Котангенс |
|---|---|---|---|---|
| 181 | -0.956 | -0.293 | -3.27 | -0.307 |
| 182 | -0.953 | -0.303 | -3.14 | -0.318 |
| 183 | -0.95 | -0.314 | -3.02 | -0.329 |
| 184 | -0.946 | -0.324 | -2.92 | -0.342 |
| 185 | -0.942 | -0.334 | -2.83 | -0.355 |
Как видно из таблицы, значения синуса уменьшаются от -0.956 до -0.942 в данном диапазоне, косинус уменьшается от -0.293 до -0.334, тангенс уменьшается от -3.27 до -2.83, а котангенс увеличивается от -0.307 до -0.355.
Зная эти значения, вы можете использовать их в различных математических и физических расчетах, а также в построении графиков и геометрических моделей.
Как пользоваться таблицей тригонометрических функций
Вот несколько советов о том, как использовать таблицу тригонометрических функций эффективно:
1. Ознакомление с таблицей
Перед использованием таблицы стоит ознакомиться с ее структурой и содержимым. Таблица включает в себя значения sin, cos, tg и ctg углов от 0 до 90 градусов.
2. Поиск нужного значения
Чтобы найти значение тригонометрической функции для определенного угла, нужно найти строку с соответствующим значением угла и столбец с нужной функцией. Затем следует прочитать значение, находящееся в пересечении выбранной строки и столбца.
3. Интерполяция
Если нужно найти значение тригонометрической функции для угла, отличного от угла в таблице, можно воспользоваться методом интерполяции. Для этого необходимо найти два ближайших значения в таблице и вычислить промежуточное значение.
4. Углы величиной более 90 градусов
Если вам нужно найти значение тригонометрической функции для угла, превышающего 90 градусов, вам потребуется использовать дополнительные свойства тригонометрии, такие как периодичность функций или применение формулы приведения. В этом случае таблица тригонометрических функций может послужить полезным исходным материалом для рассчетов.
Пример использования таблицы:
Допустим, необходимо найти значение cos 45°. Сначала находим в таблице строку с углом 45°, затем находим столбец с функцией cos. Значение, находящееся в пересечении выбранной строки и столбца, будет искомым значением. В данном случае значение cos 45° равно 0.7071.
Таблица тригонометрических функций является незаменимым инструментом для работы с углами и тригонометрическими выражениями. Правильное использование таблицы позволяет упростить вычисления и решение задач, связанных с тригонометрией.
Основные тригонометрические тождества
Основные тригонометрические тождества:
- Тождество π: sin(π) = 0, cos(π) = -1, tg(π) = 0, ctg(π) = ∞
- Тождество π/2: sin(π/2) = 1, cos(π/2) = 0, tg(π/2) = ∞, ctg(π/2) = 0
- Тождество 0: sin(0) = 0, cos(0) = 1, tg(0) = 0, ctg(0) = ∞
- Тождество 2π: sin(2π) = 0, cos(2π) = 1, tg(2π) = 0, ctg(2π) = ∞
Тригонометрические тождества позволяют выражать одну тригонометрическую функцию через другие и проводить преобразования выражений для упрощения задачи или получения новых результатов. Например, с помощью этих тождеств можно преобразовать сложные тригонометрические выражения в более простые или найти значения функций в специальных точках.
Основные тригонометрические тождества являются основой для дальнейшего изучения тригонометрии и ее приложений. Помимо перечисленных, существуют и другие тождества, которые можно применять в зависимости от конкретной задачи или потребности. Для более глубокого понимания и применения тригонометрических тождеств рекомендуется изучить специальную литературу по данной теме.
Простейшие тригонометрические уравнения
Синус и косинус
Простейшие тригонометрические уравнения могут включать следующие функции: синус (sin) и косинус (cos). Синус угла определяется отношением противоположной стороны к гипотенузе, а косинус – отношением прилежащей стороны к гипотенузе. Таким образом, синус и косинус являются основными тригонометрическими функциями.
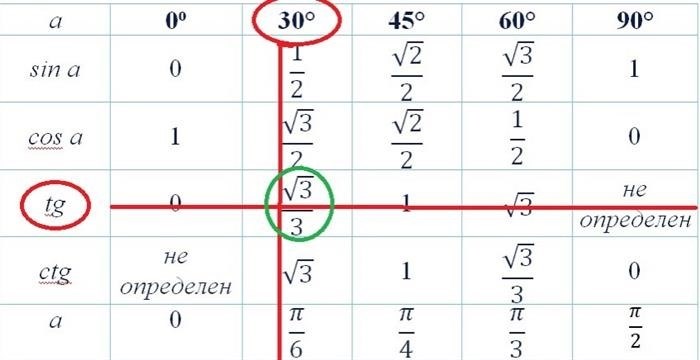
Синус и косинус – периодические функции, имеющие период 2π. Это означает, что значения синуса и косинуса повторяются через каждые 2π радиан. Простейшие тригонометрические уравнения могут быть записаны в виде равенство функции синус или косинуса угла и числа.
Примеры простейших тригонометрических уравнений
Примеры простейших тригонометрических уравнений:
- sin(x) = 0 – найдем значения угла x, при которых синус равен нулю
- cos(x) = 1/2 – найдем значения угла x, при которых косинус равен 1/2
Для решения таких уравнений необходимо знать тригонометрические свойства и уметь применять их для получения корней уравнений.
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений может быть представлено в виде таблицы:
| Уравнение | Решение |
|---|---|
| sin(x) = 0 | x = 0, π, 2π, … |
| cos(x) = 1/2 | x = π/3, 5π/3, … |
Таким образом, решение простейших тригонометрических уравнений можно представить в виде конкретных значений угла x, при которых заданная тригонометрическая функция достигает заданного значения.
Знание решения простейших тригонометрических уравнений позволяет дальше применять его для решения более сложных задач, связанных с тригонометрией и другими областями науки и техники.
Формулы двойного угла
В математике существуют формулы, которые позволяют выразить тригонометрические функции двойного угла через функции обычного угла. Эти формулы очень полезны при решении задач, связанных с треугольниками и кругами.
Основные формулы для вычисления синуса, косинуса, тангенса и котангенса двойного угла можно представить в следующем виде:
Формулы для синуса и косинуса двойного угла:
| Формула | Результат |
|---|---|
| $sin(2alpha) = 2sin(alpha)cos(alpha)$ | Выражение для синуса двойного угла через синус и косинус обычного угла |
| $cos(2alpha) = cos 2(alpha) – sin 2(alpha)$ | Выражение для косинуса двойного угла через синус и косинус обычного угла |
Формулы для тангенса и котангенса двойного угла:
| Формула | Результат |
|---|---|
| $tan(2alpha) = frac{2tan(alpha)}{1-tan 2(alpha)}$ | Выражение для тангенса двойного угла через тангенс обычного угла |
| $cot(2alpha) = frac{cot 2(alpha) – 1}{2cot(alpha)}$ | Выражение для котангенса двойного угла через котангенс обычного угла |
Формулы двойного угла широко применяются в геометрии, физике, инженерии и других науках. Они позволяют упростить вычисления и решить различные задачи, связанные с тригонометрией.
Формулы суммы и разности в тригонометрии
В тригонометрии существуют определенные формулы, которые позволяют находить значения суммы и разности тригонометрических функций. Знание этих формул может быть полезным при решении различных задач и построении графиков функций.
Формула суммы тригонометрических функций
Формула суммы позволяет выразить значение суммы двух тригонометрических функций через произведение этих функций:
sin(a + b) = sin(a) * cos(b) + cos(a) * sin(b)
cos(a + b) = cos(a) * cos(b) – sin(a) * sin(b)
tg(a + b) = (tg(a) + tg(b)) / (1 – tg(a) * tg(b))
ctg(a + b) = (ctg(a) * ctg(b) – 1) / (ctg(a) + ctg(b))
Формула разности тригонометрических функций
Формула разности позволяет выразить значение разности двух тригонометрических функций через произведение этих функций:
sin(a – b) = sin(a) * cos(b) – cos(a) * sin(b)
cos(a – b) = cos(a) * cos(b) + sin(a) * sin(b)
tg(a – b) = (tg(a) – tg(b)) / (1 + tg(a) * tg(b))
ctg(a – b) = (ctg(a) * ctg(b) + 1) / (ctg(b) – ctg(a))
Знание этих формул позволяет сократить сложность вычислений и упростить задачи, связанные с тригонометрией.
Свойства sin, cos, tg и ctg
Синус (sin)
- Значение синуса угла равно отношению длины противоположного катета к гипотенузе прямоугольного треугольника.
- Синус является нечетной функцией, то есть sin(-x) = -sin(x).
- Значение синуса ограничено интервалом от -1 до 1, то есть -1 ≤ sin(x) ≤ 1.
- Синус функция периодична с периодом 2π, то есть sin(x+2π) = sin(x).
Косинус (cos)
- Значение косинуса угла равно отношению длины прилежащего катета к гипотенузе прямоугольного треугольника.
- Косинус является четной функцией, то есть cos(-x) = cos(x).
- Значение косинуса ограничено интервалом от -1 до 1, то есть -1 ≤ cos(x) ≤ 1.
- Косинус функция также периодична с периодом 2π, то есть cos(x+2π) = cos(x).
Тангенс (tg)
- Значение тангенса угла равно отношению синуса угла к косинусу угла.
- Тангенс tg(x) равен sin(x) / cos(x).
- Тангенс является нечетной функцией, то есть tg(-x) = -tg(x).
- Тангенс может принимать любое значение, кроме значения, при котором косинус равен нулю (cos(x) ≠ 0).
Котангенс (ctg)
- Значение котангенса угла равно отношению косинуса угла к синусу угла.
- Котангенс ctg(x) равен cos(x) / sin(x).
- Котангенс также является нечетной функцией, то есть ctg(-x) = -ctg(x).
- Котангенс может принимать любое значение, кроме значения, при котором синус равен нулю (sin(x) ≠ 0).
Формулы половинного аргумента
Формулы половинного аргумента представляют собой особый набор математических формул, которые позволяют выразить значения тригонометрических функций в терминах половины значения угла.
Они часто используются для упрощения вычислений и улучшения точности результатов. Формулы половинного аргумента получаются путем редукции угла до интервала от 0 до 45 градусов или от 0 до π/4 радиан и затем применения соответствующей формулы.
Формулы половинного аргумента для sin и cos
| Уравнение | Значение sin | Значение cos |
|---|---|---|
| sin(x/2) = √[(1 – cos(x))/2] | √[(1 – cos(x))/2] | √[(1 + cos(x))/2] |
| cos(x/2) = √[(1 + cos(x))/2] | √[(1 + cos(x))/2] | √[(1 – cos(x))/2] |
Формулы половинного аргумента для tg и ctg
Для тангенса и котангенса половинного аргумента также существуют соответствующие формулы:
- tg(x/2) = sin(x)/(1 + cos(x))
- ctg(x/2) = sin(x)/(1 – cos(x))
Здесь использование формул половинного аргумента позволяет сократить число операций и получить более точные значения тригонометрических функций для половины угла.
Благодаря использованию этих формул, вычисления становятся более эффективными и удобными. Формулы половинного аргумента широко применяются в различных областях науки, инженерии и физике.
Пояснения, примеры использования
Таблица sin cos tg ctg предоставляет информацию о значениях синуса, косинуса, тангенса и котангенса для различных углов. Эти математические функции широко применяются в различных областях, включая физику, инженерию, информатику и другие науки.
Синус (sin)
Синус угла – это отношение противолежащего катета к гипотенузе в прямоугольном треугольнике. Значение синуса всегда находится в диапазоне от -1 до 1.
Пример использования:
- Вычисление высоты объекта, используя его растояние и измеренный угол подъема.
- Моделирование колебаний волн и звуковых волн.
Косинус (cos)
Косинус угла – это отношение прилегающего катета к гипотенузе в прямоугольном треугольнике. Значение косинуса также находится в диапазоне от -1 до 1.
Пример использования:
- Вычисление горизонтальной составляющей силы при заданном угле.
- Моделирование движения тела в пространстве.
Тангенс (tg)
Тангенс угла – это отношение синуса косинуса угла. Значение тангенса может быть любым числом.
Пример использования:
- Рассчет угла наклона камеры для правильного позиционирования.
- Определение высоты объекта, используя известный угол и измеренное расстояние.
Котангенс (ctg)
Котангенс угла – это обратное значение тангенса угла. Значение котангенса также может быть любым числом.
Пример использования:
- Подсчет времени оборота колеса, используя известный угол поворота.
- Определение расстояния между двумя объектами на основе измеренного угла и известной длины отрезка.
| Угол (в градусах) | sin | cos | tg | ctg |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | ∞ |
| 30° | 0.5 | √3/2 | √3/3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 0.5 | √3 | √3/3 |
| 90° | 1 | 0 | ∞ | 0 |
Соотношения между sin x, cos x и tg(x/2)
В математике существует важная связь между функциями sin(x), cos(x) и tg(x/2). Зная значения одной из этих функций, мы можем определить значения остальных функций с помощью следующих соотношений:
- sin(x) = 2 * tg(x/2) / (1 + tg 2(x/2))
- cos(x) = (1 – tg 2(x/2)) / (1 + tg 2(x/2))
- tg(x/2) = (1 – cos(x)) / sin(x)
Эти соотношения очень полезны при решении различных задач, связанных с тригонометрией. Они позволяют выразить одну функцию через другие, что упрощает вычисления и анализ функций.
Примеры использования соотношений
Предположим, нам известно значение sin(x) и мы хотим найти значения cos(x) и tg(x/2). Мы можем использовать соотношения, чтобы получить эти значения:
Пример 1:
- Пусть sin(x) = 0.5
- Используя первое соотношение, мы находим tg(x/2):
- tg(x/2) = 2 * 0.5 / (1 + 0.5 2) = 1
- Используя второе соотношение, мы находим cos(x):
- cos(x) = (1 – 1 2) / (1 + 1 2) = 0
Таким образом, если sin(x) = 0.5, то cos(x) = 0 и tg(x/2) = 1.
Пример 2:
- Пусть sin(x) = 0.8
- Используя первое соотношение, мы находим tg(x/2):
- tg(x/2) = 2 * 0.8 / (1 + 0.8 2) ≈ 1.01265
- Используя второе соотношение, мы находим cos(x):
- cos(x) = (1 – 1.01265 2) / (1 + 1.01265 2) ≈ -0.14645
Таким образом, если sin(x) = 0.8, то cos(x) ≈ -0.14645 и tg(x/2) ≈ 1.01265.
Значение соотношений
Соотношения между sin(x), cos(x) и tg(x/2) позволяют нам связать эти функции между собой и использовать их свойства при решении задач и вычислениях. Они позволяют нам выразить одну функцию через другие и обнаружить зависимости, что делает работу с тригонометрическими функциями более удобной и эффективной.
Таблица значений sin α, cos α, tg α, ctg α
Таблица со значениями синуса (sin α), косинуса (cos α), тангенса (tg α) и котангенса (ctg α) позволяет удобно и быстро находить значения этих функций для различных углов α. Зная значения в таблице, можно без необходимости использования калькулятора или математических формул быстро получить значения функций для определенного угла α.
| α | sin α | cos α | tg α | ctg α |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | ∞ |
| 30° | 1/2 | √3/2 | √3/3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | √3/3 |
| 90° | 1 | 0 | ∞ | 0 |
Используя таблицу значений sin α, cos α, tg α, ctg α, можно быстро находить значения этих функций для других углов α, не указанных в таблице. Также, таблица помогает понять свойства и зависимости между функциями и использовать их в решении математических задач.