Деление трехзначных чисел на однозначное является простым арифметическим действием, которое требует знания основных правил деления и умения выполнять элементарные вычисления. При делении трехзначного числа на однозначное необходимо следить за правильным расстановкой цифр в делении, а также учитывать возможные остатки и округления при выполнении вычислений.
Простые и составные числа
Простые числа
Простым числом называется число, которое имеет только два делителя: единицу и само себя. Простыми числами являются, например, числа 2, 3, 5, 7, 11 и т. д. Они не имеют других делителей, кроме 1 и себя самого.
Составные числа
Составное число – это число, которое имеет больше двух делителей. Составными числами являются все числа, кроме простых чисел. Они имеют несколько делителей, включая единицу, само число и дополнительные делители.
Примеры простых и составных чисел
Рассмотрим некоторые примеры простых и составных чисел:

- Простые числа: 2, 3, 5, 7, 11
- Составные числа: 4, 6, 8, 9, 10
Свойства простых чисел
Простые числа обладают некоторыми интересными и важными свойствами:
- Бесконечность: Простых чисел бесконечное множество. Это означает, что всегда можно найти новое простое число, большее любого заданного числа.
- Однозначность разложения: Любое составное число может быть представлено в виде произведения простых чисел. Это называется разложением на простые множители.
Значение простых и составных чисел
Знание о простых и составных числах имеет важное значение в математике и других областях, включая криптографию и информационную безопасность. Простые числа играют ключевую роль в шифровании и защите данных.

| Число | Тип числа |
|---|---|
| 2 | Простое число |
| 4 | Составное число |
| 7 | Простое число |
| 10 | Составное число |
Алгоритм деления в столбик
Шаги алгоритма деления в столбик:
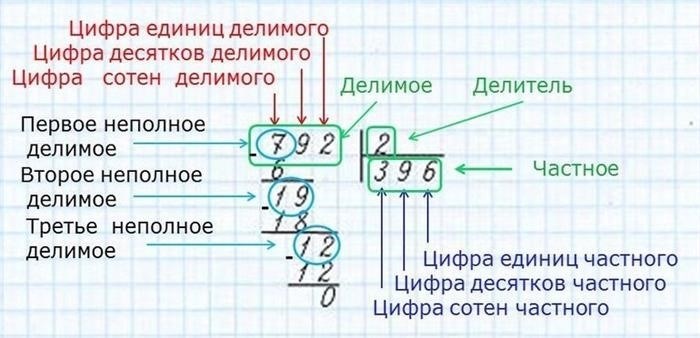
- Разделимое число записывается над делителем с выравниванием по правой стороне.
- Первая цифра делителя записывается под таким же разрядом делимого числа, чтобы полученное произведение было меньше или равно делимому числу.
- Результат произведения записывается под первой цифрой разделимого числа.
- Разделимое число вычитается из произведения и разность записывается под строчкой.
- Если разность меньше делителя, то проверяем следующую цифру разделимого числа. Если не осталось цифр, а разность все равно меньше делителя, то записываем ноль в остаток.
- Если разность больше или равна делителю, то процесс повторяется, но с учетом следующей цифры разделимого числа.
- Повторяем шаги, пока не закончатся цифры разделимого числа.
- Остаток от деления будет числом, которое осталось после выполнения всех шагов.
Пример деления в столбик:
456-----4|182416 (4*4)-----224216 (4*54)------8480 (4*20)------4
В результате деления числа 456 на число 4 получаем частное равное 114 и остаток равный 0.

Разложение на слагаемые
Для разложения числа на слагаемые, следует использовать алгебраические методы и основные свойства сложения чисел. Например, задачу можно решить с помощью регулярных математических операций или с использованием таблицы сложения однозначных чисел.
- Шаг 1: Записываем трехзначное число, которое нужно разложить на слагаемые.
- Шаг 2: Находим однозначные числа, сумма которых равна разрядному числу “сотни” трехзначного числа.
- Шаг 3: Записываем разложение числа на слагаемые, присоединяя к сотне однозначное число.
Данный метод помогает разложить трехзначное число на слагаемые и найти требуемое однозначное число при делении. Основная цель – найти слагаемые, сумма которых равна исходному числу.

Таким образом, при помощи разложения на слагаемые можно решать задачи, связанные с делением трехзначных чисел на однозначное. Этот метод помогает лучше понять основные свойства сложения чисел и найти решение к задаче.