Квадрат – это особый вид прямоугольника, у которого все стороны равны между собой. Он обладает рядом уникальных свойств и применяется в различных областях, таких как геометрия, архитектура, программирование и т.д. Квадраты широко используются в математике и на практике, например, для построения фундамента здания или для создания графических элементов интерфейса. Познакомимся ближе с этой геометрической фигурой и ее особенностями.
Что происходит в голове у шимпанзе?
Умные и социальные животные, шимпанзе, обладают развитой мыслительной деятельностью и множеством интересных способностей. Исследования позволяют нам рассмотреть, что происходит в их головах и какие задачи они могут решать.
1. Решение проблем
Шимпанзе могут анализировать ситуацию, выделять ключевые аспекты проблемы и находить решения. Они способны использовать инструменты для достижения целей, например, чтобы достать пищу из труднодоступных мест.
2. Умение планировать
Шимпанзе могут планировать свои действия и предвидеть последствия. Они могут разработать стратегию для достижения желаемого результата, например, чтобы получить доступ к еде или победить в конфликте с другим шимпанзе.
3. Эмоциональная интеллектуальность
Шимпанзе обладают эмоциональной интеллектуальностью, то есть способностью распознавать и понимать эмоции других особей. Они могут интерпретировать выражение лица или позы тела, чтобы определить настроение другого шимпанзе.
4. Социальные навыки
Шимпанзе обладают развитыми социальными навыками, они общаются между собой и могут сотрудничать в решении общих задач. Они могут устанавливать социальную иерархию и использовать ее для получения ресурсов и защиты своих интересов.
5. Понимание символов
Шимпанзе способны понимать символы и использовать их для коммуникации. Например, они могут осуществлять обучение знаковому языку и использовать жесты или символы для передачи информации другим шимпанзе.
6. Моделирование
Шимпанзе могут создавать модели предметов и событий в своих умах. Они могут представлять себе будущие события, прогнозировать, какие действия приведут к желаемому результату.
7. Интеллектуальные игры
Шимпанзе играют интеллектуальные игры, которые способствуют развитию и проверке их познавательных способностей. Они могут решать головоломки, запоминать последовательности или обучаться новым навыкам.
Пример цитаты:
«Шимпанзе обладают высоким уровнем познавательных способностей и социального интеллекта. Они умеют решать проблемы, планировать свои действия, понимать эмоции других особей, общаться и сотрудничать с другими шимпанзе. Исследования в этой области продолжаются, раскрывая все новые аспекты умственной деятельности шимпанзе».
Пример таблицы:
| Способность | Описание |
|---|---|
| Решение проблем | Анализ ситуации и нахождение решений |
| Умение планировать | Разработка стратегии и предвидение последствий |
| Эмоциональная интеллектуальность | Распознавание и понимание эмоций других особей |
| Социальные навыки | Общение и сотрудничество с другими шимпанзе |
| Понимание символов | Использование символов для коммуникации |
Чем отличается ГБОУ от МБОУ?
1. Определение и направленность
ГБОУ (государственное бюджетное общеобразовательное учреждение) – это образовательное учреждение, функционирующее на государственной или муниципальной основе. Оно предоставляет образовательные услуги по общеобразовательным программам.
МБОУ (муниципальное бюджетное общеобразовательное учреждение) – это образовательное учреждение, функционирующее на муниципальной основе и предоставляющее образовательные услуги по общеобразовательным программам.
2. Финансирование
ГБОУ получает финансирование от государства или муниципалитета, что обеспечивает оплату зарплаты работникам, закупку учебных материалов и оборудования.
МБОУ также финансируется из бюджета муниципалитета, однако объем финансирования и его эффективность могут отличаться от ГБОУ.
3. Управление и контроль
Управление ГБОУ осуществляется непосредственно государством или муниципалитетом, что дает им определенные преимущества в планировании и контроле образовательного процесса.
МБОУ управляется муниципалитетом, что может повлиять на специфику образовательного процесса и его контроля, а также обеспечивает гибкость в решении местных образовательных задач.
4. Автономия
ГБОУ может иметь большую степень автономии в принятии решений, таких как изменение образовательных программ, использование дополнительных методик и технологий обучения.
МБОУ имеет ограниченную автономию и может быть более зависимым от региональных образовательных политик и правил.
5. Профиль и специализация
ГБОУ может иметь специализацию в определенной области знаний или предлагать разнообразные профильные классы.
МБОУ может быть более универсальным и включать в себя широкий спектр предметов и направлений обучения.
6. Репутация и качество образования
ГБОУ зачастую имеет более высокую репутацию и предоставляет высокое качество образования, так как они подчиняются государственным стандартам.
МБОУ также может предоставлять качественное образование, однако уровень их репутации может варьироваться в зависимости от конкретного учреждения.
7. Месторасположение
ГБОУ может быть расположено как в городских, так и в сельских областях, что определяет доступность образования для различных категорий населения.
МБОУ чаще всего находится в муниципалитете и обслуживает население в определенной территориальной области.
8. Доступность и цена обучения
ГБОУ обычно предоставляет образование с определенными льготами и бесплатно для граждан в соответствии с законодательством.
МБОУ также может предоставлять бесплатное образование, однако некоторые услуги могут быть платными в зависимости от муниципальных норм и правил.
9. Педагогический коллектив
ГБОУ может иметь более высокую квалификацию педагогического персонала, так как они часто привлекают ведущих специалистов в области образования.
МБОУ также имеет высокие требования к квалификации преподавателей, однако их профессиональный уровень может варьироваться в зависимости от конкретного учреждения.
10. Число учеников
ГБОУ может иметь более высокую степень наполненности учащимися, так как они могут быть предпочтительными для родителей и обладать хорошей репутацией.
МБОУ может иметь различное количество учеников в зависимости от региональных и местных условий.
В итоге, ГБОУ и МБОУ – разные типы образовательных учреждений с различными особенностями, финансированием, управлением и контролем, автономией, профилем и репутацией, доступностью и другими характеристиками. Выбор между ГБОУ и МБОУ зависит от потребностей, предпочтений и возможностей родителей и учащихся.
Из чего состоит зрительный анализатор?
1. Глазные яблоки
Глазные яблоки играют ключевую роль в зрительном анализаторе. Они представляют собой шарообразные органы, заключенные в орбиты черепа. Каждый глаз состоит из следующих элементов:
- Роговица – прозрачная передняя часть глаза, которая выполняет функцию фокусировки света на сетчатку;
- Сетчатка – тонкий слой нервной ткани, на которой происходит преобразование световых сигналов в нервные импульсы;
- Хрусталик – прозрачный биологический объектив, который помогает фокусировать свет на сетчатке;
- Зрачок – отверстие в центре радужки, которое регулирует количество падающего света;
- Мышцы глаза – обеспечивают движение глазных яблок и фокусировку на объектах различных расстояний.
2. Зрительный нерв
Зрительный нерв представляет собой нервный проводник, который передает сигналы из сетчатки в мозг. Он состоит из множества нервных волокон, которые собираются вместе и направляются к зрительному корку головного мозга.
3. Зрительный корковый центр
Зрительный корковый центр – это основная область головного мозга, ответственная за анализ и интерпретацию визуальной информации. Он обрабатывает сигналы, полученные от сетчатки, и создает визуальные образы, которые мы воспринимаем.
4. Другие структуры глаза и мозга
Помимо вышеперечисленных компонентов, зрительный анализатор также включает в себя другие структуры, такие как радужка, слезные железы, стекловидное тело и мозговые области, связанные с обработкой зрительной информации.
Организация зрительного анализатора является сложным и точным механизмом, позволяющим нам воспринимать и понимать окружающий мир.
Периметр и площадь
Рассмотрим периметр и площадь прямоугольника – одной из самых простых геометрических фигур.
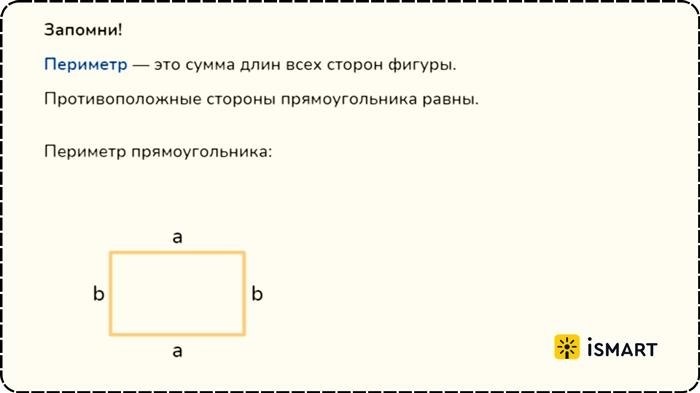
Периметр прямоугольника
Периметр прямоугольника можно вычислить по следующей формуле:
Периметр = (длина + ширина) * 2
Например, если длина прямоугольника равна 4, а ширина равна 3, то периметр будет равен (4 + 3) * 2 = 14.
Площадь прямоугольника
Площадь прямоугольника можно вычислить по следующей формуле:
Площадь = длина * ширина
Например, если длина прямоугольника равна 4, а ширина равна 3, то площадь будет равна 4 * 3 = 12.
Свойства прямоугольника
Прямоугольник обладает следующими свойствами:
- У прямоугольника все углы равны 90 градусам.
- Противоположные стороны прямоугольника параллельны и равны друг другу.
- Диагонали прямоугольника равны между собой и делят прямоугольник на два равных треугольника.
Применение периметра и площади прямоугольника
Периметр и площадь прямоугольника находят свое применение в различных областях:
- В архитектуре для расчета площади зданий и помещений.
- В строительстве для определения количества материалов, необходимых для возведения стен и покрытия пола.
- В географии для измерения площади земельных участков.
- В финансовой сфере для расчета стоимости покрытия пола или оклейки обоев.
Периметр и площадь прямоугольника являются важными показателями, которые позволяют определить размеры и форму данной геометрической фигуры. Они находят широкое применение в различных областях и способствуют решению задач, связанных с измерением и расчетом площади и периметра прямоугольника.
Как найти радиус описанной окружности около прямоугольного треугольника?
Радиус описанной окружности около прямоугольного треугольника может быть найден с использованием известных свойств и формул треугольников. Для этого можно воспользоваться теоремой описанной окружности и теоремой Пифагора.
Теорема описанной окружности
Теорема описанной окружности устанавливает, что в прямоугольном треугольнике длина гипотенузы равна диаметру описанной окружности. Таким образом, радиус описанной окружности равен половине длины гипотенузы.
Теорема Пифагора
Теорема Пифагора устанавливает, что сумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы. Исходя из этой теоремы, можно найти длину гипотенузы треугольника, а затем вычислить радиус описанной окружности.
Алгоритм поиска радиуса описанной окружности
- Найти длины катетов и гипотенузы прямоугольного треугольника.
- Используя теорему Пифагора, найти длину гипотенузы треугольника.
- Вычислить радиус описанной окружности как половину длины гипотенузы.
Пример
Пусть у нас есть прямоугольный треугольник со сторонами a = 3 и b = 4.
Используя теорему Пифагора, находим гипотенузу:
a 2 + b 2 = c 2
3 2 + 4 2 = c 2
9 + 16 = c 2

25 = c 2
c = 5
Таким образом, длина гипотенузы треугольника равна 5.
Радиус описанной окружности равен половине длины гипотенузы, то есть равен 2.5.
Используя теорему описанной окружности и теорему Пифагора, можно легко найти радиус описанной окружности в прямоугольном треугольнике. Этот метод основан на известных свойствах и формулах треугольников, и позволяет точно определить радиус описанной окружности для любого прямоугольного треугольника.
Как отличить рассуждение от повествования?
1. Цель
Одним из ключевых критериев различия между рассуждением и повествованием является цель, которую преследует автор.
- Рассуждение: целью рассуждения является выражение мнения, анализ, аргументация или построение логической цепочки рассуждений.
- Повествование: главная цель повествования – рассказать о событиях, истории или описать какой-либо объект или явление.
2. Структура
Структура текста также является важным индикатором формы изложения.
- Повествование: сюжет повествования обычно строится по канонической структуре, включающей в себя вступление, развитие событий и итог.
3. Языковые особенности
Язык текста тоже может указывать на то, какая форма изложения используется.
- Рассуждение: рассуждение обычно содержит утверждения, указывающие на мнение автора, использование аргументов и логических связей.
- Повествование: повествование часто включает в себя описание событий, действий персонажей, описание окружающей обстановки.
4. Форматирование
Оформление текста может также свидетельствовать о его форме изложения.
| Рассуждение | Повествование |
|---|---|
| Присутствие аргументов и примеров | Описание событий и деталей |
| Использование причинно-следственных связей | Последовательность действий и событий |
| Логическое построение аргументации | Описания местности, времени и персонажей |
Таким образом, анализируя цель, структуру, языковые особенности и форматирование текста, можно легко определить, является ли текст рассуждением или повествованием.
Есть ли суффикс “чик”?
Рассмотрим некоторые примеры использования суффикса “чик”:
Прозвища
- Малышчик – человек малого роста
- Сердешчик – искренний и чувствительный человек
- Толстячок – человек с избыточным весом
Имена прилагательные
- Синичкая – насекомое, которое питается семенами
- Зайчонок – молодой заяц
- Гусиничный – относящийся к гусеницам
Суффикс “чик” может быть также использован в качестве уменьшительно-ласкательной формы имени или прозвища. Например, из имени Иван может быть образовано прозвище Иванчик.
| Суффикс | Значение |
|---|---|
| чик | Форма уменьшительного сравнительной степени |
Группа крови А2: особенности и значение
Группа крови А2 имеет свои особенности и значение, которые следует учитывать при проведении медицинских процедур:
Особенности группы крови А2:
- Группа крови А2 относится к группам с антигенами А, которые присутствуют на поверхности эритроцитов.
- В группе крови А2 отсутствуют антигены В, что делает ее несовместимой с кровью группы В.
- Группа крови А2 имеет антитела к антигенам В, что может привести к агглютинации (свертыванию) крови при переливании неподходящей группы.
- Рецессивный ген А2 доминирует над другими генами группы крови.
Значение группы крови А2:
- Группа крови А2 является достаточно редкой и встречается преимущественно среди населения Японии и других регионов Восточной Азии.
- У носителей группы крови А2 может быть повышен риск развития некоторых заболеваний, таких как болезни сердца и сосудов.
- Группа крови А2 может играть роль в генетических исследованиях и определении родственных связей.
Группа крови А2 имеет свои особенности и значение, которые важно учитывать при медицинских процедурах и проведении генетических исследований.
Виды алюминия в природе
1. Бокситы
Основным рудным минералом алюминия является боксит. Бокситы – это глинистые руды, состоящие из смеси оксидов алюминия и железа. Они образуются в результате длительной химической выветривания горных пород, таких как граниты и гнейсы.
2. Каолиниты
Каолиниты – это другой распространенный тип минерала алюминия. Они представляют собой глинистые минералы, состоящие главным образом из гидратированного оксида алюминия. Каолиниты образуются за счет выветривания и разрушения силикатных горных пород, таких как сланцы и глины.
3. Корунд
Корунд – это один из самых твердых минералов и является источником драгоценных камней, таких как рубины и сапфиры. Корунд содержит алюминий в форме оксида и образуется в результате выветривания и метаморфизма гранитовых пород.
4. Кристаллический алюминий
Кристаллический алюминий – это алюминий, который образуется при высоких температурах и давлениях внутри Земли. Он может быть найден в глубоких горных породах и метеоритах.
5. Алюминиевые руды
Кроме бокситов, алюминий может быть найден в других типах руд, таких как нефелин-сиениты и карбонатиты. Эти руды встречаются в различных горных областях и могут содержать значительные количества алюминия.
6. Водные осадки
Также алюминий может находиться в воде в виде раствора или наночастиц, оседая на дне водоемов. Водные осадки могут содержать значительное количество алюминия, особенно в областях с высокой концентрацией минералов и почв.
В природе алюминий встречается в разнообразных формах, начиная от руд и минералов, таких как бокситы и каолиниты, и заканчивая кристаллическим алюминием и алюминиевыми рудами. Это указывает на обширное распространение алюминия и его значимость в мире минералогии и геологии.
Рыба: их многообразие и характеристики
Состав рыбы:
- Опорно-двигательная система: включает позвоночник, позволяющий рыбе двигаться в воде, и плавцы, которые помогают им маневрировать и подниматься в водном столбе.
- Дыхательная система: рыбы имеют жабры, через которые они получают кислород из воды и выделяют углекислый газ.
- Сердечно-сосудистая система: рыбы имеют специальный орган – сердце, которое помогает распределять кровь по всему организму. Кровь рыбы содержит гемоглобин, который отвечает за транспортировку кислорода.
- Пищеварительная система: позволяет рыбам перерабатывать пищу, получаемую как из растений, так и из других живых организмов, в питательные вещества.
- Сенсорные органы: рыбы обладают множеством чувствительных органов, таких как глаза, нюх, слух и боковая линия, позволяющая им ориентироваться в воде и обнаруживать пищу и опасность.
Роль рыбы в экосистеме:
Рыба играет важную роль в поддержании экологического баланса и функционирования водных систем. Они являются пищевым источником для многих животных, а также выполняют функцию фильтрации и контроля популяции других организмов.
Виды рыб:
| Вид рыбы | Описание |
|---|---|
| Актиноптеригии | Это класс хрящевых и костных рыб, включающий более 30 000 видов. Они отличаются присутствием плавников с радиальными лучами. |
| Лептосомы | Эта группа рыб включает длиннорылых и узкотелых видов, а также змеерылов и огромного остроносого тунца. |
| Карпообразные ryбы | Это семейство рыб, которые обитают в морях, реках и озерах. Некоторые из них также используются в промышленности как объекты рыболовства и аквакультуры. |
Рыбы представляют собой невероятно разнообразную группу животных, которые обладают уникальными адаптациями для жизни в воде. Они играют важную роль в экосистеме и являются также предметом интереса для исследования и сохранения их разнообразия и естественных сред.
Какое спряжение глагола смотреть?
Спряжение глагола “смотреть” относится к III спряжению, а именно к спряжению глаголов на -e. При спряжении глагола “смотреть” следует учитывать его особенности, такие как орфографические изменения и неправильное прошедшее время.
Основные формы глагола “смотреть”
- Инфинитив: смотреть
- Прошедшее время: смотрел
- Настоящее время: смотрю, смотришь, смотрит, смотрим, смотрите, смотрят
- Будущее время: буду смотреть, будешь смотреть, будет смотреть, будем смотреть, будете смотреть, будут смотреть
- Повелительное наклонение: смотри, смотрите
Примеры предложений с глаголом “смотреть”
Изучая спряжение глагола “смотреть”, легко составить предложения, демонстрирующие его использование:
- Он смотрит фильмы каждый вечер.
- Мы смотрим телевизор вместе.
- Ты смотришь на звезды в ночном небе.
- Я смотрю на красивый пейзаж за окном.
- Сотрудники смотрели запись с видеокамеры.
- Не смотри в свои мечты, а действуй!
- Будешь смотреть футбольный матч с нами?
Таблица спряжения глагола “смотреть”
| Лицо | Единственное число | Множественное число |
|---|---|---|
| 1 лицо | смотрю | смотрим |
| 2 лицо | смотришь | смотрите |
| 3 лицо | смотрит | смотрят |
Итак, спряжение глагола “смотреть” включает формы для каждого лица во всех временах. Зная правила спряжения, можно использовать глагол “смотреть” в своей речи и письменности четко и грамотно.
Как найти периметр прямоугольника, если ребёнок не умеет умножать?
Метод 1: Использование сложения
Периметр прямоугольника можно найти, сложив все его стороны. Если известны только значения этих сторон без их умножения, можно воспользоваться следующей формулой:
Периметр = длина стороны A + длина стороны B + длина стороны A + длина стороны B
Где длина стороны A и длина стороны B – это известные значения сторон прямоугольника.
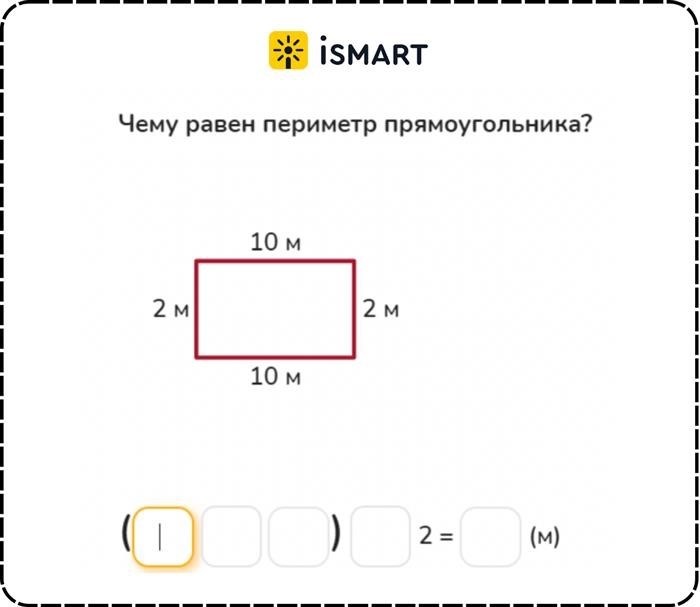
Метод 2: Использование таблицы
Другим способом для нахождения периметра прямоугольника является использование таблицы. Вы можете создать таблицу, где каждая ячейка будет соответствовать одной стороне прямоугольника. Затем, заполните значения сторон прямоугольника и сложите эти значения для получения периметра.
| Сторона | Значение |
|---|---|
| A | 10 |
| B | 6 |
В данном случае, периметр прямоугольника будет равен 32.
Метод 3: Использование графика
Вы также можете нарисовать график прямоугольника и отметить значения его сторон. Затем, можно измерить длину каждой стороны на графике и сложить эти значения для получения периметра.
Например, если длина стороны A равна 5 и длина стороны B равна 3, вы можете измерить 5 единиц на одной стороне графика и 3 единицы на другой стороне графика. Затем, сложите эти значения (5+5+3+3) и получите периметр величиной 16.
Важно помнить, что использование умножения для нахождения периметра является наиболее эффективным и точным методом. Однако, если ваш ребенок пока не освоил умножение, описанные методы помогут ему понять, как найти периметр прямоугольника.
Как найти периметр прямоугольника?
Формула для вычисления периметра прямоугольника
Для прямоугольника со сторонами a и b периметр равен удвоенной сумме длин сторон:
периметр = 2a + 2b
Шаги для вычисления периметра прямоугольника
- Определите длины сторон прямоугольника. Обозначим их a и b.
- Подставьте значения сторон в формулу периметра прямоугольника: периметр = 2a + 2b
- Выполните арифметические операции для нахождения суммы длин сторон и удвоенной суммы.
Пример вычисления периметра прямоугольника
Допустим, у нас есть прямоугольник со сторонами длиной 5 см и шириной 8 см.
Подставим значения длины и ширины в формулу периметра прямоугольника:
периметр = 2 * 5 + 2 * 8
Выполним арифметические операции:
периметр = 10 + 16
периметр = 26 см
Значение периметра прямоугольника
Периметр прямоугольника – это длина замкнутой линии, охватывающей все четыре стороны прямоугольника. Значение периметра выражается в единицах длины (например, сантиметрах или метрах) и показывает, насколько длинная линия должна быть, чтобы обойти все стороны прямоугольника.
| Примеры значений периметра | Единицы измерения |
|---|---|
| 12.6 | сантиметры |
| 0.4 | метры |
| 45 | миллиметры |
Итоги
Периметр прямоугольника можно вычислить, используя формулу периметра и значения длин его сторон. Это значение показывает длину линии, охватывающей все стороны прямоугольника. Узнав периметр прямоугольника, можно оценить его размеры и использовать эту информацию в различных математических задачах или строительных расчетах.
Прямоугольник – это
У прямоугольника есть несколько важных свойств:
- Все углы прямоугольника прямые, то есть равны 90 градусам.
- Противоположные стороны прямоугольника равны и параллельны.
- Диагонали прямоугольника равны по длине и делят фигуру на два равных треугольника.
Прямоугольники находят широкое применение в различных областях, таких как архитектура, строительство, геометрия, программирование и дизайн. Они представляют собой основу для множества других геометрических фигур и имеют ряд удобных свойств, которые делают их полезными и универсальными инструментами в работе с пространством и формой.
В итоге, прямоугольник представляет собой фигуру с четырьмя равными прямыми сторонами, прямыми углами и параллельными противоположными сторонами. Он обладает универсальностью и является основой для многих других геометрических объектов.