Порядок решения примеров по математике

Решение примеров по математике – это процесс, требующий строго выполнения определенного порядка действий. Для того чтобы получить правильный ответ, необходимо следовать определенным правилам, учитывать свойства операций и приоритеты математических операций. В данной статье мы рассмотрим основные шаги, которые помогут правильно решить примеры по математике, а также подробно изучим приоритеты математических операций и особенности их выполнения.

Решение примеров по действиям в выражениях со скобками

1. Упрощение выражений в скобках

Первый шаг в решении примеров с выражениями со скобками – упрощение выражений в скобках. Для этого необходимо выполнить операции внутри скобок независимо от остальных элементов выражения. Например, рассмотрим выражение:

2 * (3 + 4) – 5

Для его решения сначала нужно выполнить операцию в скобках:

3 + 4 = 7

Теперь у нас осталось следующее выражение:

2 * 7 – 5

2. Выполнение операций с учётом приоритета

После упрощения выражений в скобках необходимо выполнить операции с учётом приоритета. Обычно приоритет операций определяется следующим образом:

1. Выполняются операции в скобках
2. Умножение и деление
3. Сложение и вычитание

В нашем примере:

2 * 7 = 14

Теперь у нас осталось следующее выражение:

14 – 5

Вычитание:

14 – 5 = 9

3. Итоговый результат

Таким образом, решение примера “2 * (3 + 4) – 5” приводит к результату 9.

При решении примеров с действиями в выражениях со скобками необходимо помнить о правильной последовательности выполнения операций – сначала выполняются операции в скобках, затем операции с учетом приоритета. Умение правильно решать такие примеры является важной составляющей математического образования и помогает развивать логическое мышление и навыки решения сложных задач.

Основной порядок выполнения действий для простых выражений

Порядок выполнения действий:

1. Выполняются операции в скобках. Если в выражении есть скобки, необходимо сначала выполнить операции внутри них. При этом, если внутри скобок есть другие скобки, то операции во внутренних скобках выполняются первыми.
2. Выполняются операции с унарными знаками. Унарные знаки – это операции, которые применяются только к одному числу. Например, в выражении -2 выполняется операция с унарным знаком “минус” перед числом 2.
3. Выполняются операции умножения и деления. Операции умножения (*) и деления (/) имеют более высокий приоритет, чем операции сложения (+) и вычитания (-). Операции умножения и деления выполняются по порядку слева направо.
4. Выполняются операции сложения и вычитания. Операции сложения и вычитания выполняются в последнюю очередь и также выполняются по порядку слева направо.

Порядок выполнения действий позволяет упрощать выражения и получать точные результаты. Например, в выражении (2 + 3) * 4 – 5 сначала выполняется операция в скобках (2 + 3), затем результат умножается на 4, а после этого из произведения вычитается 5.

Правила выполнения действий для примеров с буквенными составляющими

Выполнение действий с примерами, содержащими буквенные составляющие, требует особого внимания и правильного подхода. Вот несколько правил, которые помогут справиться с такими примерами без лишних затруднений:

1. Понимание переменных и их значения

Перед тем, как выполнять действия с буквенными составляющими, необходимо понять значения переменных. Убедитесь, что вы знаете, какие значения могут принимать используемые буквы. Например, если дано, что а = 5, то вместо буквы “а” вы сможете подставить значение 5.

2. Выполнение операций с переменными

После того, как вы установили значения переменных, вы можете выполнить операции с ними аналогично числовым операциям. Например, если дано, что а = 5 и b = 3, то можно выполнить операцию сложения: а + b = 5 + 3 = 8.

3. Соблюдение приоритетов операций

При выполнении действий с буквенными составляющими не забывайте о приоритете операций. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Поэтому, если есть несколько операций, сначала выполните умножение и деление, а затем сложение и вычитание.

4. Раскрытие скобок

Если в примере с буквенными составляющими есть скобки, то начните, раскрывая их. Примените правила по порядку, выполняя действия внутри скобок сначала. Например, если дано (а + b) * c, то сначала выполните сложение а + b, а затем умножьте полученное значение на c.

5. Запись ответа

После выполнения всех необходимых действий с буквенными составляющими, запишите ответ в виде числа или буквенно-числового выражения в зависимости от задания.

Выполняя примеры с буквенными составляющими, помните об этих правилах и аккуратно следуйте им. Это поможет вам сделать процесс решения более понятным и легким.

Алгоритм выполнения действий первой и второй ступени

Решение математических примеров может быть организовано в несколько ступеней, каждая из которых имеет свой алгоритм действий. Первая и вторая ступени решения примеров служат для облегчения процесса вычислений и достижения точных результатов.

Первая ступень: выполнение действий с числами внутри скобок

Если в примере присутствуют скобки, необходимо выполнить действия внутри скобок первыми. Для этого следует:

• Определить, какие действия нужно выполнить внутри скобок. Могут быть сложение, вычитание, умножение и деление.
• Выполнить указанные действия с числами внутри скобок в порядке их появления. Необходимо помнить о правилах приоритетности действий: сначала умножение и деление, затем сложение и вычитание.
• Если внутри скобок есть еще скобки, повторить процедуру, начиная с первого пункта. Продолжать выполнение действий внутри скобок до тех пор, пока все скобки не будут удалены.

Вторая ступень: выполнение действий с числами вне скобок

После выполнения действий внутри скобок переходим к выполнению действий с числами, которые находятся вне скобок. Для этого следует:

1. Определить, какие действия нужно выполнить с числами вне скобок. Могут быть сложение, вычитание, умножение и деление.
2. Выполнить указанные действия с числами в порядке их появления. Необходимо помнить о правилах приоритетности действий: сначала умножение и деление, затем сложение и вычитание.

После выполнения действий первой и второй ступени, полученный результат является ответом на математический пример.

Порядок вычисления простых выражений

В математике существует определенный порядок, по которому необходимо вычислять простые выражения. Этот порядок позволяет получить верный результат и избежать ошибок.

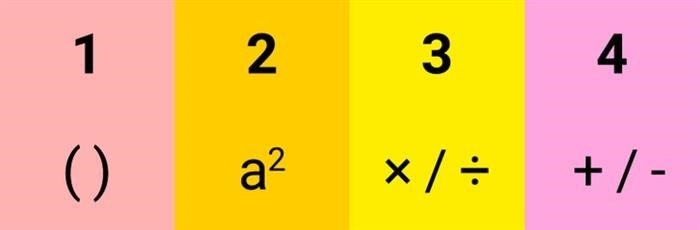
1. Скобки

Первым делом необходимо вычислить выражения внутри скобок, начиная с самых внутренних. Если в выражении есть несколько пар скобок, следует начинать с наиболее вложенных.

2. Степень

После выполняются операции со знаками степени. Если в выражении есть несколько знаков степени, обязательно выполняются они сверху вниз, начиная с наибольшей степени.

3. Умножение и деление

Затем происходят операции умножения и деления. Если в выражении есть несколько операций умножения или деления, их необходимо выполнять слева направо.

4. Сложение и вычитание

Последним этапом идут операции сложения и вычитания. Если в выражении есть несколько операций сложения или вычитания, их также выполняют слева направо.

Пример:

Дано выражение: 5 * (3 + 2 2) – 4 / 2

1. Сначала вычисляем выражение внутри скобок: 3 + 2 2 = 3 + 4 = 7
2. Далее выполняем возведение в степень: 7
3. Затем производим умножение: 5 * 7 = 35
4. И, наконец, вычитаем результат деления: 35 – 4 / 2 = 35 – 2 = 33

Порядок вычисления простых выражений в математике очень важен. Следуя определенной последовательности действий, можно гарантировать получение корректного результата. Этот порядок упрощает процесс решения примеров и помогает избежать возможных ошибок.

Варианты записи процесса вычисления выражений

Процесс вычисления математических выражений можно записывать различными способами. Это зависит от предпочтений и стиля каждого отдельного человека. Некоторые предпочитают использовать традиционные математические символы, такие как знаки “плюс”, “минус”, “умножить” и “разделить”, в то время как другие предпочитают использовать более формальные и строгие обозначения, такие как символы “+” и “-“, операторы “*” и “/”, а также скобки для обозначения порядка вычислений.

Один из вариантов записи процесса вычисления выражений – использование обратной польской записи (ОПЗ), которая использует постфиксную нотацию. В этом случае операторы записываются после операндов. Например, выражение “2 + 3” будет записано как “2 3 +”. ОПЗ облегчает вычисление выражений, так как нет необходимости использовать скобки для указания порядка операций.

Другой вариант – использование прямой польской записи (ППЗ), где операторы записываются перед операндами. Например, выражение “2 + 3” будет записано как “+ 2 3”. Это выглядит менее естественным и может быть более сложным для понимания, но также может быть полезным для автоматизации вычислений с помощью компьютерных программ.

Оба вида записи вычисления выражений имеют свои преимущества и недостатки. ОПЗ облегчает вычисления и позволяет избежать использования скобок, но может быть более сложным для восприятия и записи. ППЗ более привычна с точки зрения человека и может быть более понятна, но требует использования скобок для указания порядка операций.

Итак, вариант записи процесса вычисления выражений зависит от личных предпочтений и ситуации. Важно понимать принципы и правила математических операций, а также учитывать контекст и возможности автоматизации вычислений, чтобы выбрать наиболее удобный и эффективный способ записи выражений.