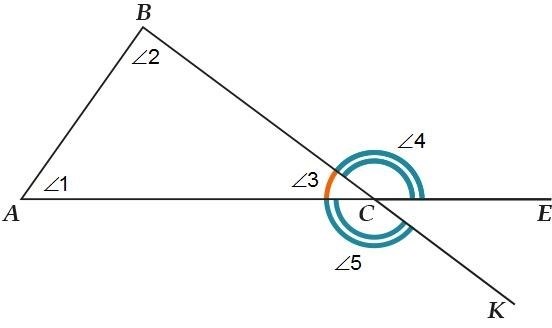
У треугольника есть интересное свойство – сумма всех его внутренних углов всегда равна одному внешнему углу.
Сумма углов треугольника. Внутренние и внешние углы
Для понимания и изучения геометрии треугольника необходимо знать основные понятия, включая сумму его углов, а также внутренние и внешние углы.
Сумма углов треугольника:
Внутри треугольника существует три угла: угол A, угол B и угол C. Они образуют сумму равную 180 градусам. Следовательно, можно сказать, что сумма внутренних углов треугольника всегда равна 180 градусам.
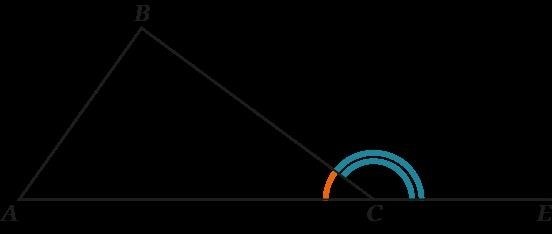
Внутренние углы треугольника:
- Угол A: это угол, образованный сторонами треугольника AB и AC.
- Угол B: это угол, образованный сторонами треугольника BC и BA.
- Угол C: это угол, образованный сторонами треугольника CA и CB.
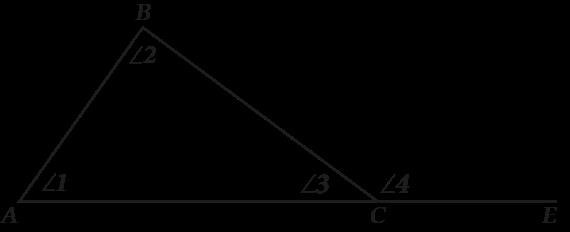
Внешние углы треугольника:
Внешние углы треугольника образуются при продолжении сторон треугольника за его пределы.
Особенности внешних углов треугольника:
- Каждый внешний угол треугольника равен сумме двух внутренних углов, не граничащих с ним.
- Сумма всех внешних углов треугольника всегда равняется 360 градусам.
| Внутренние углы треугольника: | Внешние углы треугольника: |
|---|---|
 |
 |
Таким образом, понимание суммы углов в треугольнике, а также разницы между внутренними и внешними углами помогает в изучении геометрии и решении различных задач, связанных с треугольниками.
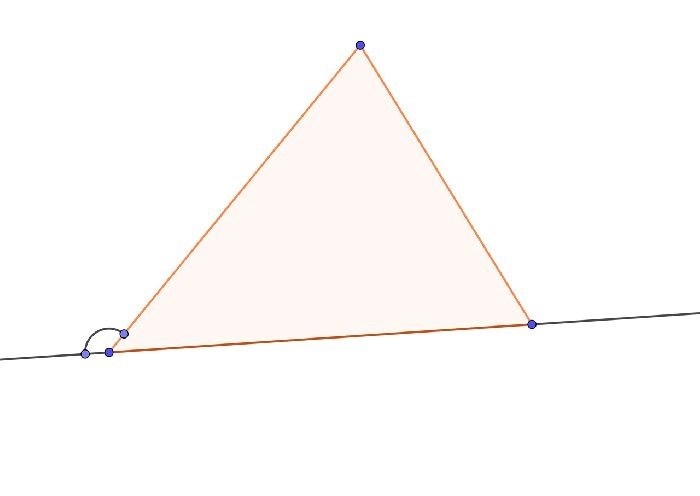
Свойства внешних углов
Свойство 1: Сумма внешних углов треугольника равна 360 градусов
Сумма всех внешних углов любого треугольника всегда равна 360 градусов. Это означает, что если мы возьмем каждый внешний угол треугольника и сложим их меры, получим именно такую сумму.
Свойство 2: Внешний угол треугольника больше любого из его внутренних углов
Внешний угол треугольника всегда больше любого из его внутренних углов. Это можно объяснить тем, что внешний угол образуется продолжением одной из сторон треугольника, а значит, измеряет больше градусов.
Свойство 3: Внешний угол треугольника и смежный внутренний угол дополняются до 180 градусов
Внешний угол треугольника и смежный с ним внутренний угол всегда дополняются до 180 градусов. Если мы сложим меры этих двух углов, получим именно такую сумму.
Свойство 4: Внешние углы треугольника равны сумме соответствующих внутренних углов с противоположной стороны
Сумма двух внешних углов треугольника, образованных продолжениями двух его сторон, всегда равна сумме соответствующих внутренних углов с противоположной стороны треугольника. Это означает, что если мы возьмем меру каждого внешнего угла и сложим их, получим меру суммы двух внутренних углов треугольника с противоположной стороны.
Эти свойства внешних углов треугольника помогают нам лучше понять его структуру и использовать это знание для решения различных геометрических задач. Изучение и понимание этих свойств является важным шагом в изучении геометрии.
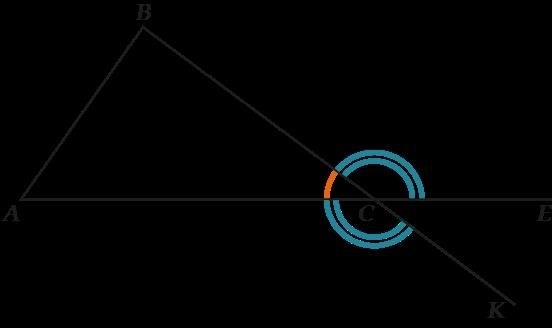
Типы треугольников и основные свойства
Прямоугольный треугольник
Прямоугольный треугольник имеет один прямой угол, равный 90 градусам. Другие два угла являются острыми. Основное свойство прямоугольного треугольника заключается в том, что квадрат длины гипотенузы равен сумме квадратов длин катетов:
c² = a² + b²
где c – гипотенуза, a и b – катеты.
Равнобедренный треугольник
Равнобедренный треугольник – это треугольник, у которого две стороны равны. Также равнобедренный треугольник имеет два равных угла. Основное свойство равнобедренного треугольника заключается в том, что высота, проведенная из вершины равна стороне, деленной пополам:
h = a/2
где h – высота треугольника, a – сторона.
Равносторонний треугольник
Равносторонний треугольник – это треугольник, у которого все стороны равны. Углы равностороннего треугольника равны 60 градусам. Основное свойство равностороннего треугольника заключается в том, что высота, проведенная из вершины, делит треугольник на два равных равнобедренных треугольника:
“Высота, проведенная из вершины равностороннего треугольника, является его биссектрисой, медианой и высотой одновременно.”
Сумма углов треугольника
Внешний угол треугольника равен сумме его внутренних углов. Это основное свойство треугольника, которое можно использовать для решения различных геометрических задач. Сумма всех углов треугольника равна 180 градусам.
| Тип треугольника | Особенности |
|---|---|
| Прямоугольный треугольник | Один прямой угол |
| Равнобедренный треугольник | Две равные стороны и два равных угла |
| Равносторонний треугольник | Все стороны равны, все углы равны 60 градусам |
Треугольник – коротко о главном
Составные элементы треугольника
Каждый треугольник состоит из следующих элементов:
- Стороны: треугольник имеет три стороны, которые соединяют его вершины.
- Углы: треугольник имеет три угла, обозначаемых буквами A, B и C.
- Вершины: точки пересечения сторон треугольника образуют его вершины.
Типы треугольников
В зависимости от длин сторон и величины углов, треугольники могут быть классифицированы следующим образом:
| Тип треугольника | Описание |
|---|---|
| Равносторонний | Все стороны равны по длине. |
| Равнобедренный | Две стороны равны по длине. |
| Прямоугольный | Один из углов равен 90 градусам. |
| Остроугольный | Все углы треугольника меньше 90 градусов. |
| Тупоугольный | Один из углов больше 90 градусов. |
Свойства треугольника
У треугольника есть некоторые важные свойства, которые помогают в его изучении и расчетах:
- Сумма углов: сумма всех углов треугольника равна 180 градусам.
- Сумма длин сторон: сумма длин любых двух сторон треугольника всегда больше третьей стороны.
- Равенство треугольников: треугольники с равными соответствующими сторонами и углами считаются равными.
- Неравенство треугольников: ни одна из сторон треугольника не может быть больше суммы двух других сторон.
Изучение и понимание основных свойств и характеристик треугольника играет важную роль в геометрии и других математических дисциплинах. Оно помогает в решении задач, проведении измерений и анализе геометрических форм.
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов. Он имеет различные типы, свойства и характеристики, которые являются основой для его изучения и понимания.

Что мы узнали?
Мы также разобралися с понятиями внешних и внутренних углов треугольника. Внешний угол треугольника образуется продолжением одной из его сторон за вершиной, в то время как внутренние углы треугольника образуются внутри треугольника у его вершин.
Также мы рассмотрели доказательство теоремы о внешнем угле треугольника, основанное на свойствах параллельных прямых и соответственных углов. Это доказательство является классическим примером использования геометрических конструкций и логических рассуждений.
- Мы узнали, что внешний угол треугольника равен сумме его внутренних углов.
- Мы поняли различие между внешними и внутренними углами треугольника.
- Мы изучили доказательство теоремы о внешнем угле треугольника.
Знание данной теоремы позволяет решать различные задачи геометрии, а также облегчает понимание свойств и закономерностей треугольников. Она является одним из фундаментальных понятий геометрии и широко применяется в решении задач аналитической и синтетической геометрии.