Для перехода от логарифма с одним основанием к другому существует формула, которая позволяет легко и быстро осуществить эту операцию. Формула перехода к новому основанию логарифма позволяет выразить значение логарифма с новым основанием через значение логарифма с другим основанием и обратно. Это очень полезное свойство логарифмов, которое позволяет упростить многие математические выкладки и решение уравнений.
Что такое логарифм?
Основной принцип логарифма основывается на свойствах степеней и позволяет упростить математические вычисления и решение сложных задач. Использование логарифмов нашло широкое применение в науке, технике, финансах, а также в различных областях жизни.
Формула логарифма
Формула логарифма выглядит следующим образом:
logb(x) = y
Здесь:
- log – логарифм;
- b – основание логарифма;
- x – аргумент;
- y – значение логарифма.
Таким образом, логарифм от числа x по основанию b равен y.
Свойства логарифмов
Логарифмы обладают рядом свойств, которые позволяют сократить сложные вычисления или получить необходимую информацию о числе:
- Логарифм произведения равен сумме логарифмов: logb(xy) = logb(x) + logb(y);
- Логарифм частного равен разности логарифмов: logb(x/y) = logb(x) – logb(y);
- Логарифм от степени равен произведению логарифма на показатель степени: logb(xn) = n * logb(x);
- Логарифм от корня равен частному логарифмов: logb(√(x)) = 1/2 * logb(x);
- Логарифм от основания равен единице: logb(b) = 1;
- Логарифм от числа 1 равен нулю: logb(1) = 0.
Примеры применения
Логарифмы широко используются в различных областях, включая:
- Финансы – для расчета сложных процентов и оценки доходности инвестиций;
- Наука – для представления больших и малых чисел и работы с экспоненциальными функциями;
- Техника – для решения задач в электротехнике, телекоммуникациях, компьютерной графике;
- Медицина – для оценки статистических данных и измерения концентрации веществ в организме;
- Музыка – для настройки музыкальных инструментов и создания музыкальных гамм;
- Статистика – для анализа данных и расчета вероятностей событий.
Знание логарифмов позволяет упростить сложные операции и решение математических задач, а также применять их в различных областях науки и жизни.
Применение логарифмических свойств в примерах
1. Упрощение выражений
Одно из основных применений логарифмических свойств – упрощение сложных выражений. Зачастую, замена сложных операций на логарифмические свойства позволяет существенно упростить выражение и упрощает его анализ. Например, рассмотрим следующее выражение:
loga(xm) – loga(yn)
Используя свойство разности логарифмов, это выражение можно упростить до:
loga(xm/yn)
2. Решение уравнений
Логарифмические свойства применяются для решения уравнений, содержащих логарифмы. Например, рассмотрим следующее уравнение:
loga(x) + loga(y) = loga(z)
Используя свойство суммы логарифмов, мы можем объединить два логарифма в один:
loga(xy) = loga(z)
Теперь, применив свойство равенства логарифмов, мы можем найти значение переменной xy:
xy = z
3. Преобразование уравнений и неравенств
Логарифмические свойства также могут использоваться для преобразования уравнений и неравенств. Например, рассмотрим следующую неравенство:
loga(x) > c
Используя свойство неравенства логарифма, мы можем переписать это неравенство в исходной системе:
x > ac
Таким образом, мы получили новое уравнение, которое представляет исходную систему.

4. Расчет сложных функций и их графиков
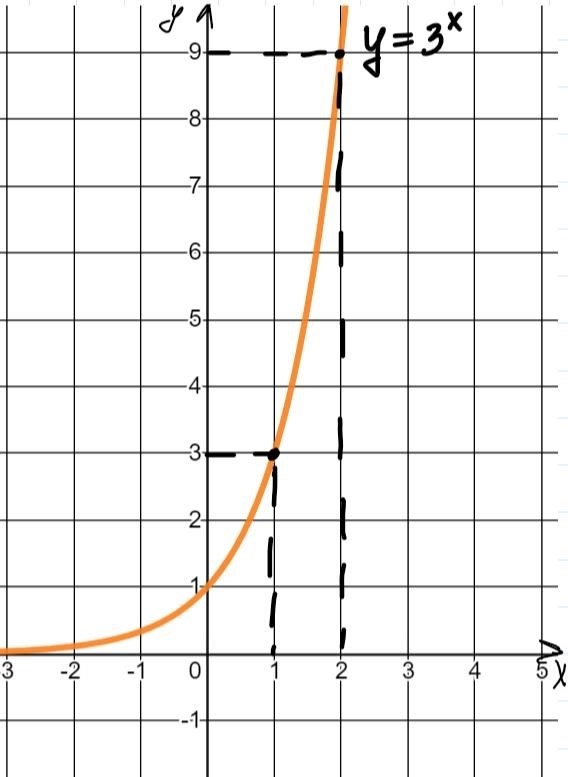
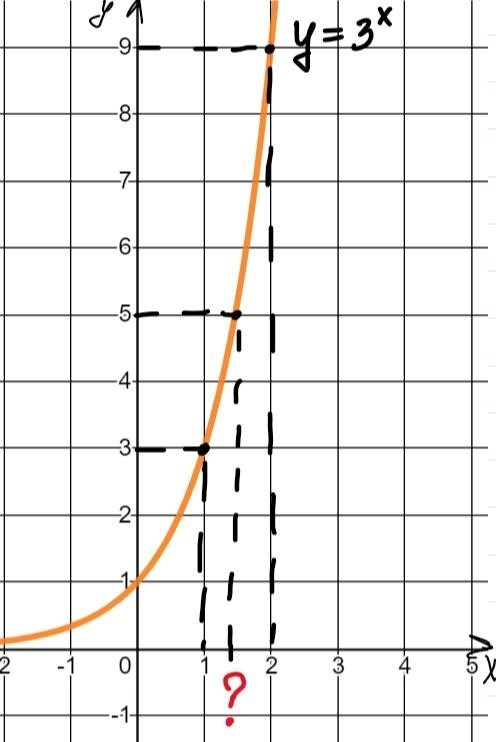
С помощью логарифмических свойств можно рассчитывать сложные функции и строить их графики. Например, рассмотрим функцию вида:
y = aloga(x)
График этой функции будет проходить через точку (1, 1) и будет являться убывающей функцией для x < 1 и возрастающей для x > 1.
5. Применение в финансовых расчетах
Логарифмические свойства имеют применение и в финансовых расчетах, таких как расчет процентной ставки, сложных процентов и дисконтирования. Например, формула для расчета сложных процентов может быть выражена с использованием логарифмических свойств:
S = P(1 + r/n)nt
где S – конечная сумма, P – начальная сумма, r – процентная ставка, n – количество периодов в году, t – общее количество лет.
Логарифмические свойства представляют собой мощный инструмент для работы с логарифмами и находят применение в различных областях знаний. Они позволяют упрощать выражения, решать уравнения, преобразовывать системы неравенств, расчитывать сложные функции и проводить финансовые расчеты.
Как решать примеры с логарифмами?
1. Изучите основные свойства логарифмов
- Логарифм от произведения равен сумме логарифмов;
- Логарифм от частного равен разности логарифмов;
- Логарифм от степени равен произведению степени на логарифм исходного числа.
Пример: $log_2(4 cdot  = log_2(4) + log_2(8)$
= log_2(4) + log_2(8)$
2. Примените формулу перехода к новому основанию логарифма
Если вам дано выражение с логарифмом по неизвестному основанию, формула перехода к новому основанию может помочь. Формула выглядит следующим образом:
$log_a(x) = frac{log_b(x)}{log_b(a)}$

Пример: $log_2(8) = frac{log_{10}(8)}{log_{10}(2)}$
3. Упростите логарифмическое выражение с помощью правил логарифмов
Используйте свойства логарифмов для упрощения выражения. Основная цель – сократить сложные выражения до более простых форм.
Пример: $log_3(27) = log_3(3 3) = 3log_3(3) = 3 cdot 1 = 3$
4. Решите уравнение с логарифмом
Если вам дано уравнение с логарифмом, используйте свойства логарифмов для перевода его в экспоненциальную форму. Затем решите уравнение, используя обратные операции.
Пример: $log_2(x) = 4$
Переводим в экспоненциальную форму: $2 4 = x$, откуда $x = 16$
5. Проверьте результат
Проверьте полученный результат, подставив его обратно в исходное уравнение или выражение с логарифмом.
Пример: Подставим $x = 16$ в исходное уравнение $log_2(x) = 4$, получим $log_2(16) = 4$.
| Исходное выражение | Результат |
|---|---|
| $log_2(8 cdot 16)$ | $log_2(8)+log_2(16) = 3 + 4$ |
| $log_5(125) = log_5(5 3)$ | $3log_5(5) = 3 cdot 1 = 3$ |
Следуя этим шагам и используя свойства и формулы логарифмов, вы сможете решать примеры с логарифмами с легкостью.
Практическое применение логарифмов
Рассмотрим несколько практических примеров применения логарифмов:
1. Финансовые расчеты
Логарифмы активно используются в финансовых расчетах, таких как определение процента доходности, оценка инвестиций и определение стоимости акций. Логарифмическая шкала позволяет увидеть процентные изменения в процентах, а не в абсолютных значениях.
2. Экспоненциальный рост и упадок
В различных областях науки, включая биологию, экономику и физику, логарифмы используются для анализа экспоненциального роста и упадка. Они позволяют определить скорость изменения величины и предсказать будущие тенденции.
3. Компьютерные науки
Логарифмы широко применяются в компьютерных науках, особенно в анализе производительности алгоритмов. Они помогают оценить сложность алгоритма и выбрать наиболее эффективный подход для решения задачи.
4. Аккуратный представление чисел
Использование логарифмов позволяет представить большие или малые числа в удобной форме. Например, при измерении уровня звука, логарифмическая шкала децибел позволяет сравнивать различные уровни интенсивности звука.
5. Пропорциональное масштабирование
Логарифмы используются для масштабирования графиков и диаграмм, чтобы представить данные на одинаковом уровне детализации. Таким образом, разница в значениях на графике будет интерпретироваться с одинаковым уровнем точности.
| Область применения | Примеры задач |
|---|---|
| Финансы | Оценка доходности инвестиций, расчет стоимости акций |
| Наука | Анализ экспоненциального роста и упадка, изучение физических процессов |
| Компьютерные науки | Анализ производительности алгоритмов, оптимизация программного обеспечения |
Логарифмы позволяют упростить сложные вычисления, а также анализировать и предсказывать различные процессы и явления в различных областях науки и техники.
Какие бывают виды логарифмов?
Существует несколько видов логарифмов, каждый из которых имеет свои особенности и применения. Рассмотрим некоторые из них:
1. Обычные логарифмы
Обычные логарифмы обозначаются как logb(x), где b – основание логарифма, а x – число, для которого мы ищем логарифм. Основание логарифма может быть любым положительным числом, кроме 1, и определяет систему счисления логарифма.
2. Натуральные логарифмы
Натуральные логарифмы – это логарифмы с основанием e, где e – основание натуральных логарифмов, равное примерно 2.71828. Они обозначаются как ln(x) или loge(x). Натуральные логарифмы широко используются в математическом анализе и теории вероятностей.
3. Двоичные логарифмы
Двоичные логарифмы (логарифмы по основанию 2) обозначаются как log2(x). Они наиболее часто используются в информатике и компьютерных науках, где биты и байты являются основой для измерения информации и объема данных.
4. Десятичные логарифмы
Десятичные логарифмы (логарифмы по основанию 10) обозначаются как log10(x). Они нашли широкое применение в научных и инженерных расчетах, где часто используется система счисления по основанию 10.
5. Обратные логарифмы
Обратные логарифмы – это специальные функции, которые позволяют найти число, для которого логарифм равен заданному значению. Например, если logb(x) = y, то обратный логарифм по основанию b будет равен x = by.
Виды логарифмов имеют свои особенности и применения в различных областях знания. Знание этих особенностей позволяет более эффективно применять логарифмы при решении задач и проведении исследований.
Свойства и формулы логарифмов: итог
В этой статье мы рассмотрели основные свойства логарифмов и формулы, позволяющие выполнять различные операции с ними. Мы начали с определения логарифма как степени, к которой нужно возвести основание, чтобы получить заданное число. Затем мы изучили основное свойство логарифмов – их способность преобразовывать сложение в умножение и вычитание в деление.
Мы рассмотрели формулу перехода к новому основанию и узнали, как можно преобразовывать логарифмы с различными основаниями. Эта формула особенно полезна при использовании таблицы логарифмов со стандартным основанием.
Также мы изучили и другие важные свойства логарифмов, такие как свойства изменения порядка, свойство равенства, свойства степени, свойства обратной функции логарифма и свойство суммы.
Используя эти свойства и формулы, мы можем упрощать сложные выражения, решать уравнения, проводить анализ данных и многое другое.
Таким образом, логарифмы являются мощным математическим инструментом, который имеет широкое применение в различных областях. Изучение свойств и формул логарифмов поможет улучшить наши навыки решения задач и проведения исследований.