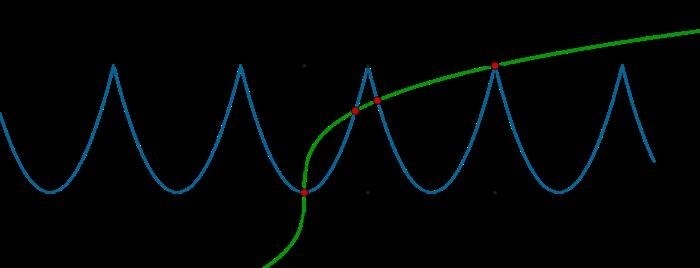
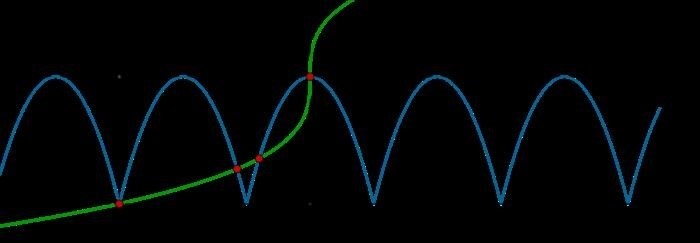
В математике существуют функции, которые нельзя отнести ни к четным, ни к нечетным. Такие функции называются ни четными, ни нечетными функциями. В отличие от четных функций, которые симметричны относительно оси ординат, и нечетных функций, которые симметричны относительно начала координат, ни четные, ни нечетные функции не обладают никакой символической симметрией. Они имеют свои особенности и используются в различных областях математики и физики.
Наибольшее и наименьшее значение функции на промежутке
Наибольшее значение функции
Наибольшее значение функции на промежутке – это максимальное значение, которое функция может принимать в данной области. Для нахождения наибольшего значения функции необходимо найти точку экстремума и проверить ее значение.
- Если точка экстремума является локальным максимумом, то ее значение будет наибольшим значением функции на данном промежутке.
- Если функция не имеет локальных максимумов, то необходимо проверить значения функции на концах промежутка. Если значение на одном из концов больше, чем на другом, то это будет наибольшее значение функции.
Наименьшее значение функции
Наименьшее значение функции на промежутке – это минимальное значение, которое функция может принимать в данной области. Аналогично нахождению наибольшего значения функции, для определения наименьшего значения необходимо найти точку экстремума и проверить ее значение.
- Если точка экстремума является локальным минимумом, то ее значение будет наименьшим значением функции на данном промежутке.
- Если функция не имеет локальных минимумов, то необходимо проверить значения функции на концах промежутка. Если значение на одном из концов меньше, чем на другом, то это будет наименьшее значение функции.
Таким образом, нахождение наибольшего и наименьшего значения функции на промежутке позволяет определить ее поведение в данной области и выявить особенности ее графика.
Функция общего вида
Что такое четная функция?
Четная функция – это функция, которая обладает особой симметрией. Если для любого значения x в области определения функции f(x) значение f(-x) равно f(x), то функция называется четной. Например, функция f(x) = x 2 является четной функцией, так как f(-x) = (-x) 2 = x 2 = f(x).
Что такое нечетная функция?
Нечетная функция – это функция, которая обладает особой симметрией. Если для любого значения x в области определения функции f(x) значение f(-x) равно -f(x), то функция называется нечетной. Например, функция f(x) = x 3 является нечетной функцией, так как f(-x) = (-x) 3 = -x 3 = -f(x).
Функция общего вида не проявляет ни четные, ни нечетные свойства на всей области определения. Она может быть симметричной относительно начала координат на одном отрезке и несимметричной на другом отрезке. Например, функция f(x) = x 2 + 3 на отрезке [-2, 2] является симметричной относительно начала координат, так как f(-x) = (-x) 2 + 3 = x 2 + 3 = f(x), а на отрезке [-2, 0] функция является несимметричной.
Функция общего вида может иметь различные особенности и разнообразные формы графиков, что делает ее интересной для изучения и анализа. Такие функции широко используются в различных областях науки и техники для моделирования и предсказания различных явлений.
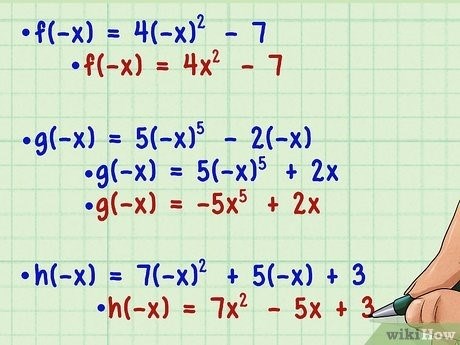
График чётной и нечётной функции
График чётной и нечётной функции в математике представляет собой визуальное представление зависимости значения функции от её аргумента. График позволяет оценить свойства функции, в том числе её чётность или нечётность.
Чётная функция:
- Значение функции симметрично относительно оси ординат.
- График чётной функции одинаков на интервалах, симметричных относительно оси ординат.
- Примером чётной функции является y = x².
Нечётная функция:
- Значение функции симметрично относительно начала координат.
- График нечётной функции одинаков на интервалах, симметричных относительно начала координат.
- Примером нечётной функции является y = x³.
На графике чётной функции можно заметить:
- Отсутствие точек экстремума, так как функция симметрична.
- Чётное число пересечений с осью ординат.
- Симметричность графика относительно оси ординат.
На графике нечётной функции можно заметить:
- Возможное наличие точки экстремума, так как функция симметрична относительно начала координат.
- Нечётное число пересечений с осью ординат.
- Симметричность графика относительно начала координат.
График чётной и нечётной функции помогает визуализировать особенности функции, такие как её симметрия и количество пересечений с осями. Это очень полезно при решении математических задач и анализе функций в дальнейшем.
Возрастающая и убывающая функция
В математике существует понятие возрастающей и убывающей функции. Они помогают нам понять, как изменяется значение функции при изменении аргумента.
Возрастающая функция
Возрастающая функция – это функция, которая увеличивает свое значение при увеличении аргумента. Если для любых двух значений аргумента x1 и x2, при условии x1 < x2, соответствующие значения функции f(x1) и f(x2) также удовлетворяют условию f(x1) < f(x2), то функция является возрастающей.
Убывающая функция
Убывающая функция наоборот уменьшает свое значение при увеличении аргумента. Если для любых двух значений аргумента x1 и x2, при условии x1 < x2, соответствующие значения функции f(x1) и f(x2) также удовлетворяют условию f(x1) > f(x2), то функция является убывающей.
Итак, мы разобрались с понятием возрастающей и убывающей функции. Теперь, когда вы встретите данные термины в контексте математических выражений или задач, вы будете знать, что они означают и как их определить.