Упрощение логических выражений является важной частью математической логики и программируемых электронных устройств. Оно позволяет упростить сложные выражения, устранить избыточность и улучшить их читаемость. В данной статье мы предлагаем несколько примеров дешифровки и решения логических выражений, чтобы получить простые и легко понятные результаты.
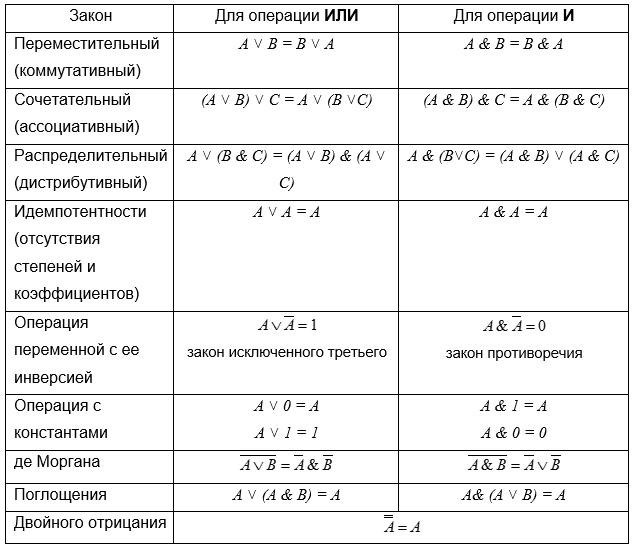
Законы алгебры логики
Законы идемпотентности
- Закон двойного отрицания: двойное отрицание выражения равно самому выражению: ¬(¬A) = A
- Закон исключения третьего: выражение A или ¬A всегда истинно: A ∨ ¬A = 1
- Закон исключения четвертого: выражение A и ¬A всегда ложно: A ∧ ¬A = 0
Законы ассоциативности
- Закон ассоциативности конъюнкции: выражение A ∧ (B ∧ C) эквивалентно (A ∧ B) ∧ C: A ∧ (B ∧ C) = (A ∧ B) ∧ C
- Закон ассоциативности дизъюнкции: выражение A ∨ (B ∨ C) эквивалентно (A ∨ B) ∨ C: A ∨ (B ∨ C) = (A ∨ B) ∨ C
| Заголовок 1 | Заголовок 2 |
|---|---|
| Ячейка 1 | Ячейка 2 |
| Ячейка 3 | Ячейка 4 |
Законы дистрибутивности
Законы дистрибутивности помогают раскрыть скобки в логических выражениях:
- Закон дистрибутивности дизъюнкции относительно конъюнкции: A ∨ (B ∧ C) эквивалентно (A ∨ B) ∧ (A ∨ C): A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)
- Закон дистрибутивности конъюнкции относительно дизъюнкции: A ∧ (B ∨ C) эквивалентно (A ∧ B) ∨ (A ∧ C): A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C)
Применение законов алгебры логики позволяет упрощать сложные логические выражения и улучшать их читаемость и понимаемость. Важно помнить, что применение законов алгебры логики должно быть логически обосновано и корректно исполнено.
Подписи к слайдам:
На протяжении данной статьи мы рассмотрели основные принципы упрощения логических выражений и изучили примеры с их решением. Мы рассмотрели различные методы сокращения логических операций и использовали законы алгебры логики для упрощения выражений.
В ходе статьи мы узнали, что упрощение логических выражений может быть полезным во многих областях, включая программирование, алгоритмы и электронику. Упрощенные выражения позволяют уменьшить сложность кода, сделать его более понятным и улучшить производительность программы или устройства.
Мы рассмотрели несколько основных методов упрощения логических выражений, включая использование законов дистрибутивности, ассоциативности и коммутативности, а также правил де Моргана.
Важно понимать, что упрощенные логические выражения могут иметь меньше операций и операндов, что значительно упрощает их анализ и работу с ними. Однако, при упрощении выражений также необходимо учитывать их семантику, чтобы не изменить истинное значение выражения.