Высказывание в информатике – это одно или несколько логически связанных утверждений, которые можно оценить как истинные или ложные. Высказывания играют важную роль в программировании, так как позволяют контролировать ход выполнения программы, принимая решения на основе их значений. В информатике существует несколько типов высказываний, таких как логические операторы, сравнение значений и условные выражения. Понимание того, что такое высказывание, является основой для работы с логикой и алгоритмами в программировании.
Как определить истинность или ложность простого высказывания?
1. Анализ смысла высказывания
Первый способ определения истинности или ложности высказывания основан на его смысле. Если высказывание соответствует фактам или правилам логики, оно считается истинным. Если же высказывание противоречит фактам или правилам логики, оно считается ложным.
2. Использование логических операций
- Логическое “И” (AND): высказывание истинно, только если оба операнда истинны.
- Логическое “ИЛИ” (OR): высказывание истинно, если хотя бы один из операндов истинен.
- Логическое “НЕ” (NOT): меняет истинность высказывания на противоположную.
3. Проверка с помощью таблицы истинности
Таблица истинности – это удобный способ систематизировать значения истинности высказывания в зависимости от значений его составляющих.
| Высказывание | Истинность |
|---|---|
| p | true |
| q | false |
| p И q | false |
| p ИЛИ q | true |
| НЕ p | false |
4. Использование формальных методов
Определение истинности или ложности простого высказывания в информатике является важной задачей. Различные методы и критерии позволяют проводить такую оценку с высокой степенью точности и достоверности, что является основой для разработки эффективных алгоритмов и систем на основе логического мышления.

Основные операции алгебры логики
Операция конъюнкции (И)
Операция конъюнкции, обозначаемая символом &, объединяет два логических выражения и возвращает истинное значение только в том случае, когда оба выражения истинны. В противном случае, возвращает ложное значение.
Операция дизъюнкции (ИЛИ)
Операция дизъюнкции, обозначаемая символом |, объединяет два логических выражения и возвращает истинное значение, если хотя бы одно из выражений истинно. Если оба выражения ложны, операция дизъюнкции вернет ложное значение.
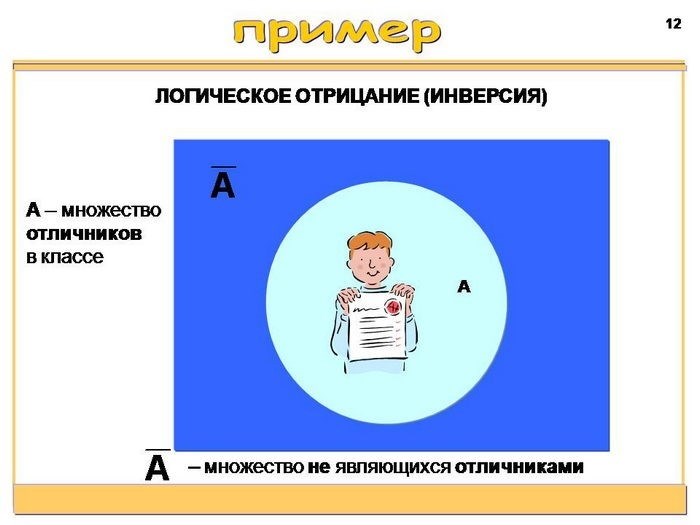
Операция отрицания (НЕ)
Операция отрицания, обозначаемая символом ¬ или !, изменяет значение логического выражения на противоположное. Если выражение истинно, операция отрицания вернет ложное значение, и наоборот.
Операция импликации (ЕСЛИ…ТО)
Операция импликации, обозначаемая символом ⇒, связывает два логических выражения и возвращает истинное значение в случае, если первое выражение ложно или второе выражение истинно. В противном случае, операция импликации вернет ложное значение.
Таблица истинности
| Выражение A | Выражение B | A И B | A ИЛИ B | ¬A | A ⇒ B |
|---|---|---|---|---|---|
| Истина | Истина | Истина | Истина | Ложь | Истина |
| Истина | Ложь | Ложь | Истина | Ложь | Ложь |
| Ложь | Истина | Ложь | Истина | Истина | Истина |
| Ложь | Ложь | Ложь | Ложь | Истина | Истина |
Таблица истинности демонстрирует результаты операций алгебры логики в зависимости от значений входных логических выражений A и B.
Основные операции алгебры логики позволяют выполнять логические операции на компьютере и строить логические схемы. Понимание и использование этих операций является фундаментальным для работы с информацией и программирования.
Какие существуют основные логические операции?
1. Операция “И” (AND)
Операция “И” возвращает истину только в том случае, если оба операнда являются истиной. Если хотя бы один из операндов является ложью, то результат будет ложью.
2. Операция “ИЛИ” (OR)
Операция “ИЛИ” возвращает истину, если хотя бы один из операндов является истиной. Если оба операнда являются ложью, то результат будет ложью.
3. Операция “НЕ” (NOT)
Операция “НЕ” меняет логическое значение на противоположное. Если операнд равен истине, то результат будет ложью, и наоборот.
4. Операция “Исключающее ИЛИ” (XOR)
Операция “Исключающее ИЛИ” возвращает истину, если один из операндов является истиной, но не оба одновременно. Если оба операнда равны истине или лжи, результат будет ложью.
5. Операция импликации (→)
Операция импликации возвращает истину, если условие истинно, а результат не имеет значения или является истиной. В противном случае результат будет ложью.
6. Операция эквиваленции (↔)
Операция эквиваленции возвращает истину, если оба операнда равны друг другу. Если операнды различаются, результат будет ложью.

| Операнд 1 | Операнд 2 | AND | OR | NOT | XOR | → | ↔ |
|---|---|---|---|---|---|---|---|
| Истина | Истина | Истина | Истина | Ложь | Ложь | Истина | Истина |
| Истина | Ложь | Ложь | Истина | Ложь | Истина | Ложь | Ложь |
| Ложь | Истина | Ложь | Истина | Истина | Истина | Истина | Ложь |
| Ложь | Ложь | Ложь | Ложь | Истина | Ложь | Истина | Истина |
Важно помнить, что в информатике и логике логические операции используются для выражения условий, проверок и построения логических цепочек, которые позволяют создавать сложные алгоритмы и программы.
Как запомнить порядок выполнения логических операций
Логические операции играют важную роль в программировании, поэтому важно знать правильный порядок их выполнения. Ниже приведены несколько способов, помогающих запомнить порядок выполнения логических операций.
1. Запомните акроним
Акронимы полезны при запоминании последовательностей. В случае порядка выполнения логических операций, можно использовать акроним НИКИЛОН. Каждая буква этого слова соответствует определенной операции:
- Н – НЕ (отрицание)
- И – И (логическое “и”)
- К – КЕ (исключающее “или”)
- И – ИЛИ (логическое “или”)
- Л – ЛОГ (логическое “и” с присваиванием)
- О – ОТР (отрицание с присваиванием)
- Н – НИ (логическое “не”)
Запоминая этот акроним, вы сможете легко вспомнить порядок выполнения логических операций.
2. Используйте таблицу
Другой способ запомнить порядок выполнения логических операций – использование таблицы. В таблице указывается порядок операций от наиболее высокого приоритета до наименьшего. Ниже приведена таблица с порядком операций:
| Операция | Приоритет |
|---|---|
| НЕ (отрицание) | Наивысший |
| И (логическое “и”) | Выше |
| КЕ (исключающее “или”) | Выше |
| ИЛИ (логическое “или”) | Ниже |
| ЛОГ (логическое “и” с присваиванием) | Ниже |
| ОТР (отрицание с присваиванием) | Ниже |
| НИ (логическое “не”) | Наименьший |
Используя эту таблицу, можно легко определить порядок выполнения логических операций.
Зная правильный порядок выполнения логических операций, вы сможете эффективно работать с логическими выражениями в программировании. Применяйте акроним или таблицу, чтобы удобно запомнить порядок операций.
Как определить высказывание?
Признаки высказывания:
- Высказывание должно быть полным и иметь однозначное значение.
- Высказывание должно быть ясным и понятным.
- Высказывание должно иметь определенный смысл и быть возможным для проверки.
- Высказывание должно быть самодостаточным и не зависеть от контекста.
- Высказывание должно быть либо истиным, либо ложным.
Примеры высказываний:
- “Солнце взойдет завтра в 6 часов утра.” Это высказывание является полным и имеет определенный смысл. Оно также может быть проверено на истинность.
- “Я люблю мороженое.” Это высказывание является ясным и понятным, но не может быть проверено на истинность, так как это субъективное заявление.
Высказывания и логические операции:
Высказывания могут быть комбинированы с помощью логических операций, таких как “и”, “или” и “не”.
| Логическая операция | Пример | Истинность |
|---|---|---|
| И | Высказывание А и высказывание Б | Истинно, если оба высказывания истинны |
| ИЛИ | Высказывание А или высказывание Б | Истинно, если хотя бы одно высказывание истинно |
| НЕ | не высказывание А | Истинно, если высказывание А ложно |
Используя комбинации высказываний с логическими операциями, можно создавать более сложные логические выражения и условия для программирования и работы с информацией в компьютерных системах.
Что такое логические множества
Логические множества позволяют описывать группы элементов и операции, которые могут быть выполнены над ними. Они основаны на основных принципах логики и множественного анализа, таких как объединение, пересечение, разность и дополнение.
Основные понятия в логических множествах:
- Элемент: отдельный объект или значение, принадлежащий множеству;
- Множество: совокупность элементов, объединенных общим свойством;
- Пустое множество: множество, не содержащее ни одного элемента;
- Универсальное множество: множество, содержащее все возможные элементы;
- Подмножество: множество, все элементы которого принадлежат другому множеству;
- Операции над множествами: объединение, пересечение, разность и дополнение.
Операции над множествами:
| Операция | Обозначение | Описание |
|---|---|---|
| Объединение | A ∪ B | Множество, состоящее из всех элементов, которые принадлежат хотя бы одному из указанных множеств |
| Пересечение | A ∩ B | Множество, состоящее из всех элементов, которые принадлежат одновременно указанным множествам |
| Разность | A B | Множество, состоящее из всех элементов, которые принадлежат первому множеству, но не принадлежат второму множеству |
| Дополнение | A’ | Множество, состоящее из всех элементов, которые не принадлежат указанному множеству |
Логические множества имеют широкие применения в информатике. Они используются для построения алгоритмов, оптимизации баз данных, поиска и сравнения информации, а также для решения логических задач и доказательства теорем. Важно уметь использовать эти понятия правильно и грамотно для эффективной работы с информацией в информатике.

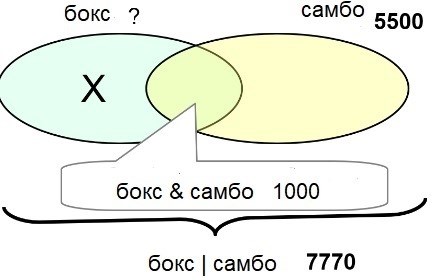
Что такое круги Эйлера
Круги Эйлера помогают наглядно представить пересечения и отношения между различными множествами. Они позволяют легко выявить общие элементы, уникальные элементы и количество элементов в каждом множестве.
Основные принципы кругов Эйлера
- Каждый круг представляет отдельное множество или группу элементов.
- Площадь пересечения кругов показывает количество общих элементов между множествами.
- Размер каждого круга указывает на количество элементов в соответствующем множестве.
- Круги Эйлера могут иметь пересечения, что означает наличие общих элементов между несколькими множествами.
Пример кругов Эйлера
Давайте рассмотрим пример использования кругов Эйлера для визуализации связей между тремя множествами: A, B и C.
| A | B | C | |
| Множество 1 | 10 элементов | 5 элементов | 3 элемента |
| Множество 2 | 7 элементов | 5 элементов | 2 элемента |
| Множество 3 | 4 элемента | 2 элемента | 3 элемента |
Из этой таблицы можно сделать следующие наблюдения:
- Множество A содержит 10 элементов, множество B содержит 5 элементов, а множество C содержит 3 элемента.
- Пересечение между множествами A и B содержит 5 элементов, между множествами A и C – 3 элемента, а между B и C – 2 элемента.
- Также существует общий элемент, который присутствует во всех трех множествах.
Использование кругов Эйлера позволяет с легкостью определить отношения и пересечения между множествами, что является ценным инструментом в информатике, исследовании данных и визуализации связей между элементами.
Что такое алгебра логики в информатике?
Законы алгебры логики
- Законы идемпотентности: операции ИЛИ и И примененные к одному и тому же значению дают то же самое значение.
- Законы коммутативности: порядок операндов при операциях ИЛИ и И не имеет значения.
- Законы ассоциативности: результат операций ИЛИ и И не зависит от их расстановки круглых скобок при наличии более двух операций.
- Законы дистрибутивности: операции ИЛИ и И связаны законами дистрибутивности в отношении друг друга.
- Законы отрицания: отрицание отрицания любого значения равно исходному значению.
Примеры использования алгебры логики в информатике
Алгебра логики широко применяется в информатике для решения различных задач:
- Разработка и оптимизация логических схем для построения электронных схем и компьютерных схематических диаграмм.
- Анализ и формулирование математических моделей для описания работы алгоритмов и программ.
- Создание и разработка баз данных, используя логические операции ИЛИ, И и НЕ.
- Разработка и оптимизация алгоритмов поиска и фильтрации данных.
- Управление и контроль логических операций в программных системах.
Преимущества алгебры логики в информатике
Использование алгебры логики в информатике имеет ряд преимуществ:
- Позволяет проводить логический анализ и оценку различных типов информации.
- Облегчает процесс проектирования и разработки компьютерных систем и программных продуктов.
- Позволяет улучшить эффективность и оптимизировать процессы обработки и управления информацией.
- Позволяет улучшить качество и надежность программных систем, основанных на логических принципах.
Алгебра логики является основой для изучения и применения различных логических концепций и методов в информатике. Она позволяет анализировать и управлять информацией различных типов, что делает ее неотъемлемой частью информационных технологий.
Высказывание в информатике: основные понятия и примеры
Основные понятия:
- Высказывание: утверждение, которое может быть верным или ложным.
- Истинное высказывание: высказывание, которое является истинным.
- Ложное высказывание: высказывание, которое является ложным.
- Предикат: функция, которая принимает одно или несколько значений и возвращает истину или ложь.
- Логическая операция: операция, выполняющая операции с высказываниями и дающая результат в виде истинного или ложного значения.
Примеры высказываний в информатике:
- “2 + 2 = 4” – это истинное высказывание, так как результат сложения двух чисел равен 4.
- “3 > 5” – это ложное высказывание, так как утверждение “3 больше 5” является неверным.
- “x > 10” – это предикатное высказывание, которое зависит от значения переменной x.
Примеры логических операций:
| Логическая операция | Пример | Результат |
|---|---|---|
| И | true И true | true |
| ИЛИ | true ИЛИ false | true |
| НЕ | НЕ true | false |
Высказывания в информатике являются важным инструментом для работы с логическими операциями и условиями в компьютерных программах. Они позволяют программистам создавать алгоритмы, которые могут принимать решения и выполнять действия в зависимости от истинности или ложности определенных условий. Понимание основных понятий и использование высказываний помогает разработчикам писать эффективный и надежный код.
Пирамида приоритетов: как определить важность и срочность задач
Как работает пирамида приоритетов?
Пирамида приоритетов строится на основе двух основных факторов: важности и срочности задачи. Важность задачи определяется степенью ее влияния на достижение целей и результатов, в то время как срочность задачи определяется временными рамками исполнения.
В основе пирамиды лежат четыре уровня приоритетов:
- Срочные и важные задачи
- Важные, но не срочные задачи
- Срочные, но не важные задачи
- Ни срочные, ни важные задачи
1. Срочные и важные задачи
Это задачи, которые требуют немедленного внимания и являются ключевыми для достижения целей. Они имеют большое значение и могут иметь серьезные последствия, если не будут выполнены вовремя. Такие задачи должны быть выполнены в первую очередь.
2. Важные, но не срочные задачи
Это задачи, которые важны для достижения целей, но не имеют жестких сроков исполнения. Они требуют хорошего планирования и могут быть выполнены в более удобное время. Такие задачи следует выполнить после срочных и важных задач.
3. Срочные, но не важные задачи
Это задачи, которые требуют мгновенного внимания, но не являются ключевыми для достижения целей. Они могут отвлекать и занимать время, но не приносят существенных результатов. Такие задачи лучше делегировать или отложить.
4. Ни срочные, ни важные задачи
Это задачи, которые не требуют немедленного внимания и не относятся к ключевым целям. Они могут быть отложены или вообще исключены из списка задач.
Пример использования пирамиды приоритетов
Рассмотрим пример использования пирамиды приоритетов:
| Задача | Важность | Срочность | Приоритет |
|---|---|---|---|
| Подготовить отчет для важного клиента | Высокая | Срочная | 1 |
| Провести собрание с командой | Высокая | Не срочная | 2 |
| Отправить приглашение на мероприятие | Низкая | Срочная | 3 |
| Получить подарок для коллеги | Низкая | Не срочная | 4 |
Исходя из примера, видно, что задача подготовки отчета для важного клиента имеет самый высокий приоритет (1), так как она является и срочной, и важной. Задача проведения собрания с командой имеет второй приоритет (2), так как она важная, но не срочная. Остальные задачи имеют меньший приоритет в соответствии с их важностью и срочностью.
Используя пирамиду приоритетов, мы можем организовать свою работу и использовать свое время более эффективно. Постоянное обновление пирамиды позволит нам контролировать приоритеты и достигать лучших результатов в своей деятельности.
Что такое конъюнкция кратко?
В информатике конъюнкция часто обозначается символом “И” или “&&”. Когда мы используем конъюнкцию, то проверяем, верны ли оба условия. Если оба условия истинны, то результат будет истинным, в противном случае – ложным.
Примеры использования конъюнкции:
- Условие 1 И условие 2
- if (условие 1 && условие 2) { выполнить действие }
Конъюнкция используется для проверки нескольких условий одновременно. Она может быть полезной при программировании для создания более сложных условий и принятия решений на основе нескольких факторов.
Таблица истинности конъюнкции:
| Условие 1 | Условие 2 | Результат |
|---|---|---|
| Истина | Истина | Истина |
| Истина | Ложь | Ложь |
| Ложь | Истина | Ложь |
| Ложь | Ложь | Ложь |
Применение конъюнкции позволяет учесть несколько условий и принять решение на основе их совместного выполнения. Это удобно в программировании для создания более сложных логических выражений и контроля поведения программы.
Как выглядит логическая структура сложного высказывания
Логическая структура сложного высказывания представляет собой упорядоченное описание основных элементов и связей, которые составляют это высказывание. Эта структура позволяет логически организовать информацию и представить ее в удобной и понятной форме.
Прежде чем описывать логическую структуру сложного высказывания, необходимо понять, что такое простое высказывание. Простое высказывание – это утверждение о состоянии или отношении объектов или их характеристик в определенный момент времени. Простое высказывание может быть истинным или ложным.
Логическая структура сложного высказывания
Логическая структура сложного высказывания состоит из следующих элементов:
- Операторы логических связей – это специальные слова или символы, которые позволяют связать два или более простых высказывания. Примеры операторов: “и”, “или”, “не”, “если…то”, “тогда…”.
- Простые высказывания – это основные элементы, из которых состоит сложное высказывание. Они могут быть истинными или ложными и могут представлять собой утверждения о фактах или отношениях между объектами.
Примеры логической структуры сложного высказывания
| Высказывание | Логическая структура |
|---|---|
| Если сегодня идет дождь, то улица будет мокрой. | Если…то |
| Джон и Питер танцуют. | И |
| Я не пойду на прогулку, потому что сегодня холодно. | потому что |
Как записывать и читать логические выражения
Запись логических выражений
Логические выражения состоят из логических операторов, операндов и скобок. Они используются для сравнения значений и возвращения результата в виде логического значения “истина” или “ложь”.
- Логические операторы: AND, OR, NOT.
- Операнды: переменные или константы, которые сравниваются.
- Скобки: используются для управления порядком выполнения операций.
Примеры логических выражений:
(x > 5) AND (y < 10)(a == b) OR (c != d)NOT (p AND q)
Чтение логических выражений
При чтении логических выражений важно понимать порядок выполнения операций и правила приоритета операторов.
Приоритет операторов:
- Логический оператор NOT имеет самый высокий приоритет и выполняется первым.
- Затем выполняются операторы AND.
- Самым последним выполняется оператор OR.
Примеры чтения логических выражений:
| Выражение | Чтение |
|---|---|
(x > 5) AND (y < 10) |
"Если x больше 5 И y меньше 10" |
(a == b) OR (c != d) |
"Если a равно b ИЛИ c не равно d" |
NOT (p AND q) |
"Если НЕ (p И q)" |
Важно помнить, что при достижении истинного значения в логическом выражении, остальные операции в нем не выполняются, поскольку результат уже ясен.
Запись и чтение логических выражений являются важными навыками для программистов. Они позволяют создавать условия и принимать решения в программном коде на основе определенных критериев.

Логические выражения – это основа для создания умных алгоритмов и логической логики программ. Они позволяют программам принимать различные решения в зависимости от заданных условий. Правильная запись и чтение логических выражений являются фундаментальными навыками для программистов и исследователей в области информационных технологий.
Необязательные в школьной программе операции
В школьной программе информатики обычно преподают основные операции, такие как сложение, вычитание, умножение, деление и т.д. Однако существуют и другие операции, которые могут быть необязательными для изучения в рамках учебного курса, но при этом могут быть полезными и интересными для учащихся.
1. Возведение в степень
Операция возведения в степень позволяет увеличить число в указанную степень. Это особенно полезно при работе с большими числами или в алгоритмах, где необходимо многократно умножать число на само себя. Понимание и использование этой операции может значительно упростить решение некоторых задач.
2. Деление с остатком
Операция деления с остатком позволяет разделить одно число на другое и получить остаток от деления. Она может быть полезна при решении задач, связанных с распределением ресурсов или проверкой делимости чисел. Также она позволяет понять, как работает операция деления и что деление не всегда даёт целый результат.
3. Битовые операции
Битовые операции позволяют работать с отдельными битами в числах. Они полезны при работе с двоичной системой счисления, а также в задачах, связанных с манипуляцией и проверкой битовой информации. Например, с помощью битовых операций можно определить, является ли число степенью двойки или выполнить быстрое умножение или деление на 2.
4. Строковые операции
Строковые операции позволяют работать с текстовыми данными. Они позволяют объединять, разделять и изменять строки, а также выполнять поиск и замену подстрок. Строковые операции могут быть полезными при работе с данными в текстовом формате, например, при обработке логов или анализе пользовательского ввода.
5. Работа с файлами
Операции работы с файлами позволяют считывать и записывать данные из/в файлы. Они могут быть полезными при работе с внешними данными, например, при чтении и записи информации из базы данных или текстовых файлов. Понимание этих операций позволит учащимся освоить основы работы с внешними источниками данных.
| Операция | Описание |
|---|---|
| Возведение в степень | Увеличение числа в указанную степень |
| Деление с остатком | Разделение числа на другое с остатком |
| Битовые операции | Работа с битами в числах |
| Строковые операции | Работа с текстовыми данными |
| Работа с файлами | Чтение и запись данных из/в файлы |
Необязательные в школьной программе операции, такие как возведение в степень, деление с остатком, битовые операции, строковые операции и работа с файлами, могут дополнить базовые навыки учащихся и помочь им в решении более сложных задач. Они открывают новые возможности и расширяют область применения информатики, позволяя ученикам развивать свои навыки и интересы в этой области.
Графическое изображение логических множеств с помощью кругов Эйлера
Круги Эйлера используются для представления множеств в виде пересекающихся кругов. Каждый круг соответствует одному или нескольким множествам, и их пересечения отображаются в виде области, где круги пересекаются. Этот метод позволяет визуально увидеть, какие элементы принадлежат разным множествам и какие элементы являются общими для нескольких множеств.
При использовании кругов Эйлера важно правильно расположить круги и области пересечения, чтобы точно отразить отношения между множествами. Каждый круг должен быть уникальным и не пересекаться с другими кругами вне областей пересечения. Это помогает четко определить каждое множество и его относительное место в общей структуре.
Круги Эйлера широко применяются для визуализации информации в различных областях, таких как анализ данных, маркетинговые исследования, биология, социология и т.д. Они помогают прояснить отношения между различными группами элементов и делают сложные данные более доступными и понятными.
Использование кругов Эйлера при визуализации логических множеств позволяет наглядно представить их структуру и отношение друг к другу. Этот метод является эффективным инструментом для анализа данных и принятия решений на основе этих данных.