Треугольники считаются подобными, если их соответствующие стороны пропорциональны, а соответствующие углы равны между собой. Подобие треугольников является важным понятием в геометрии и используется для решения различных задач, таких как определение отношения площадей или нахождение пропорциональных отрезков на сторонах треугольника. Понимание признаков и свойств подобных треугольников позволяет упростить решение задач и проведение геометрических вычислений.
Подобные треугольники – подробнее
Вот основные свойства и характеристики подобных треугольников:
1. Углы
В подобных треугольниках соответствующие углы равны. Это означает, что если два треугольника подобны, то их углы будут иметь одинаковые величины.
2. Стороны
Соответствующие стороны подобных треугольников пропорциональны. Это означает, что если одну из сторон одного треугольника умножить на определенное число, то она будет равна соответствующей стороне другого треугольника.

3. Похожесть
Подобные треугольники называют также “похожими” треугольниками. Это связано с тем, что они имеют одинаковую форму, но могут различаться размерами. Можно сказать, что один треугольник является уменьшенной или увеличенной копией другого треугольника.
4. Коэффициент подобия
Коэффициентом подобия двух треугольников называется число, на которое нужно умножить длины сторон одного треугольника, чтобы получить соответствующие стороны другого треугольника. Коэффициент подобия обозначается символом “k”.
5. Отношение площадей
Площади подобных треугольников связаны отношением произведения соответствующих сторон этих треугольников. Если длины сторон подобных треугольников обозначить как “a”, “b” и “c”, то отношение их площадей будет равно квадрату коэффициента подобия: (S1/S2) = k 2.
6. Применение
Подобные треугольники находят применение в различных областях, включая архитектуру, геодезию, физику и технику. Они используются для расчёта высот зданий, внешних и внутренних углов, а также для создания трехмерных моделей объектов.
7. Теория
Теория подобных треугольников основывается на постулатах Евклида и принципах геометрии. Доказательство подобия треугольников может быть основано на различных свойствах и теоремах, таких как теорема Синусов и теорема Пифагора.
Подобие двух треугольников: признаки и свойства
Признаки подобия треугольников:
- Угловой признак: если у двух треугольников все углы соответственно равны, то они подобны.
- Признак по длинам сторон: если все стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника, то они подобны.
- Признак по пропорциональным отрезкам: если прямая, соединяющая вершины двух подобных треугольников и параллельная одной из сторон, делит противоположную сторону на два отрезка, пропорциональных соответствующим сторонам другого треугольника, то они подобны.
Свойства подобия треугольников:
- Соответствующие углы подобных треугольников равны.
- Соответствующие стороны подобных треугольников пропорциональны.
- Отношение площадей подобных треугольников равно квадрату отношения длин соответствующих сторон.
- Если два треугольника подобны, то их высоты, опущенные к соответствующим основаниям, также подобны.
Пример использования теоремы подобия треугольников:
Допустим, у нас есть треугольник ABC с известными сторонами AB, BC и AC, и вершинами A(1, 2), B(3, 4) и C(5, 6). Мы хотим найти размеры подобного треугольника A’B’C’. По теореме о подобии треугольников, мы можем использовать пропорции длин сторон, чтобы найти соответствующие размеры. Например, если AB = 3, то A’B’ будет равно 6, если мы знаем, что сторона A’B’ в 2 раза длиннее стороны AB.
| Треугольник ABC | Треугольник A’B’C’ |
|---|---|
| AB = 3 | A’B’ = 6 |
| BC = 4 | B’C’ = 8 |
| AC = 5 | A’C’ = 10 |
Таким образом, мы можем использовать подобие треугольников для нахождения неизвестных размеров треугольников на основе заданных размеров. Это полезное свойство, которое применяется в различных областях, таких как архитектура, инженерия и физика.
Теорема об отношении площадей
Формулировка теоремы:
Если два треугольника подобны, то отношение площадей этих треугольников равно квадрату отношения длин соответствующих сторон.
Иначе говоря, если треугольники АВС и МНО подобны, то можно написать следующее соотношение:
S(АВС) : S(МНО) = (АВ/МН) 2 = (ВС/НО) 2 = (АС/МО) 2
Где S(АВС) и S(МНО) – площади треугольников АВС и МНО соответственно, АВ/МН, ВС/НО, АС/МО – отношения длин соответствующих сторон.
Теорема является важным инструментом для вычисления площадей подобных фигур. Она позволяет сократить время и упростить процесс подсчета площадей, используя отношения длин сторон.
Теорема об отношении площадей широко применяется в различных областях, включая архитектуру, строительство, геодезию, картографию и другие. Она позволяет решать задачи связанные с подсчетом площадей различных фигур, основываясь на знании их подобия.
Некоторые свойства и следствия
Свойства подобных треугольников:
- Углы подобных треугольников равны между собой.
- Соответствующие стороны подобных треугольников пропорциональны.
- Отношение длин сторон подобных треугольников называется коэффициентом подобия и обозначается как k.
- Если два треугольника подобны, то их площади относятся как квадраты соответствующих сторон.
Следствия от свойств подобных треугольников:
- Если в треугольнике проведены высоты из двух подобных к нему треугольников, то эти высоты имеют одинаковую пропорциональность по отношению к сторонам основания.
- Если в треугольнике проведены медианы из двух подобных к нему треугольников, то эти медианы имеют одинаковую пропорциональность по отношению к сторонам основания.
- Если в треугольнике проведены биссектрисы из двух подобных к нему треугольников, то эти биссектрисы имеют одинаковую пропорциональность по отношению к сторонам основания.
- Если треугольник подобен своему собственному образу, он называется самоподобным треугольником.
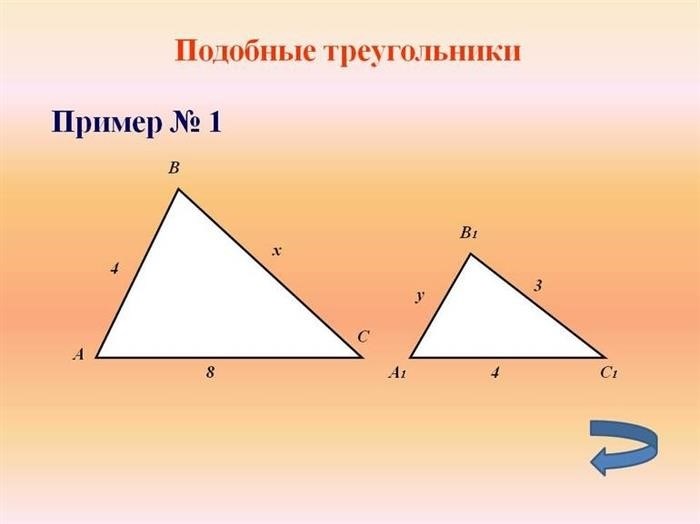
Пример:
Рассмотрим два подобных треугольника.
| Треугольник ABC | Треугольник DEF |
|---|---|
| AB = 4 см | DE = 2 см |
| BC = 6 см | EF = 3 см |
| AC = 8 см | DF = 4 см |
Из приведенной таблицы видно, что соответствующие стороны подобных треугольников пропорциональны соотношением 2:1. Это означает, что треугольник DEF является уменьшенной копией треугольника ABC.
Подобие треугольников имеет множество применений как в геометрии, так и в других областях, таких как физика, архитектура и техническое моделирование. Познание и понимание свойств и следствий подобных треугольников позволяет решать сложные задачи и строить точные модели.
Признаки подобия треугольников
Определение подобия треугольников
Два треугольника считаются подобными, если соответствующие углы в них равны, а соответствующие стороны пропорциональны.
Признаки подобия треугольников
- Угловой признак: Если два треугольника имеют два равных угла, то они подобны.
- Признак по длинам сторон: Если все стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника, то они подобны.
- Признак по длинам двух сторон и углу: Если две стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника, а угол между этими сторонами равен, то треугольники подобны.
- Признак по углам: Если два угла одного треугольника равны двум углам другого треугольника, то они подобны.
Свойства подобных треугольников
- Соответствующие углы подобных треугольников равны. Это свойство позволяет нам установить подобие треугольников, сравнивая их углы.
- Пропорциональность сторон подобных треугольников. Если треугольники подобны, то их соответствующие стороны пропорциональны. Это позволяет нам определить неизвестные стороны, используя известные значения их пропорций.
- Соотношение площадей подобных треугольников. Площадь подобных треугольников относится квадратично к соответствующим сторонам. Если соотношение длин сторон двух треугольников равно k, то соотношение площадей будет равно k 2.
Подобие треугольников является важным инструментом в геометрии, который позволяет нам решать различные задачи, связанные с треугольниками. Знание признаков и свойств подобия треугольников поможет нам эффективно работать с ними и использовать их в приложениях повседневной жизни.
Что мы узнали?
1. Условия подобия треугольников
- Два треугольника подобны, если их соответствующие углы равны.
- Два треугольника подобны, если их стороны пропорциональны. Это означает, что отношения длин сторон одного треугольника к длинам соответствующих сторон другого треугольника равны.
2. Основные свойства подобных треугольников
- Соответствующие стороны подобных треугольников пропорциональны.
- Соответствующие углы подобных треугольников равны.
- Площади подобных треугольников относятся как квадраты соответствующих сторон.
3. Применение подобия треугольников
- Подобие треугольников применяется в геометрии для решения задач связанных с нахождением неизвестных сторон и углов треугольников.
- Подобие треугольников используется в строительстве, архитектуре и дизайне для создания пропорциональных форм и конструкций.
4. Расчеты подобных треугольников
Для расчетов подобных треугольников используются следующие формулы:
| Формула | Описание |
|---|---|
| Формула подобия по углам: | Углы треугольников равны |
| Формула подобия по сторонам: | Отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника равно |
| Формула расчета длины стороны: | Длина стороны треугольника равна произведению соответствующей стороны другого треугольника на отношение длин сторон этих треугольников |
| Формула расчета площади: | Площадь треугольника равна произведению квадрата стороны на соответствующую сторону другого треугольника |
В результате исследования мы узнали о условиях подобия треугольников, их свойствах, а также о возможностях их применения в различных областях.
Подобие треугольников – коротко о главном
Основные свойства подобных треугольников:
- Углы двух подобных треугольников равны.
- Длины соответствующих сторон подобных треугольников пропорциональны.
- Подобные треугольники можно строить по разным масштабам.
Подобие треугольников важно для решения различных задач и применяется в различных областях, включая строительство, геодезию, архитектуру и дизайн. Знание свойств подобных треугольников позволяет анализировать геометрические формы и создавать сбалансированные и пропорциональные конструкции.
Главные теоремы о подобии треугольников:
- Теорема 1: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы при одинаково направленных сторонах равны, то треугольники подобны.
- Теорема 2: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
- Теорема 3: Если в треугольнике две стороны пропорциональны двум сторонам другого треугольника и углы при этих сторонах равны, то треугольники подобны.
Важно уметь распознавать подобные треугольники, использовать свойства подобия для нахождения дополнительных углов или сторон, а также анализировать пропорциональность и соответствие между сторонами и углами. Знание подобия треугольников поможет в решении сложных геометрических задач и повысит общую геометрическую грамотность.
Как доказать подобие треугольников
Ниже приведены несколько способов, которые помогут вам доказать подобие треугольников:
1. Критерий по стороне-стороне-стороне (ССС)
Если соответствующие стороны двух треугольников пропорциональны, то треугольники подобны. Для доказательства подобия, вам необходимо сравнить пропорции всех трех сторон.
2. Критерий по углу-стороне-углу (УСУ)
Если два треугольника имеют два соответствующих равных угла и пропорциональные стороны между этими углами, то они подобны. Для доказательства подобия, вам необходимо сравнить углы и пропорции сторон.
3. Критерий по углу-углу-стороне (УУС)
Если два треугольника имеют два соответствующих равных угла и одну равную сторону между этими углами, то они подобны. Для доказательства подобия, вам необходимо сравнить углы и стороны.
4. Критерий по стороне-углу-стороне (СУС)
Если два треугольника имеют одну равную сторону, равный угол между этой стороной и смежной стороной, и пропорционально соответствующие стороны, то они подобны. Для доказательства подобия, вам необходимо сравнить стороны, углы и пропорции сторон.

| Критерий | Соответствующие элементы треугольников |
|---|---|
| ССС | Стороны |
| УСУ | Углы и стороны |
| УУС | Углы и сторона |
| СУС | Сторона, угол и сторона |
Важно помнить, что для доказательства подобия, необходимо сравнить все соответствующие элементы двух треугольников. Это позволит установить, являются ли они подобными. Используйте вышеперечисленные критерии и методы для доказательства подобия треугольников и в дальнейшем применяйте их в решении геометрических задач.
Самый главный «секрет» подобия треугольников
Однако самый главный «секрет» подобия треугольников заключается в их соответствии. Два треугольника считаются подобными, если все их углы равны между собой. Это означает, что необходимо, чтобы каждый угол одного треугольника был равен соответствующему углу другого треугольника.
Соответствие углов является ключевым фактором при определении подобия треугольников, поскольку оно гарантирует равенство соответствующих сторон и пропорциональность между ними. Именно на основе этого свойства можно строить дальнейшие рассуждения и анализировать геометрические задачи.
Подобие треугольников играет важную роль в различных областях науки и техники. Например, в архитектуре оно позволяет создавать пропорциональные и эстетически приятные постройки, в оптике и медицине – определять подобные геометрические формы, а в аэродинамике – проектировать аэропланы с улучшенными характеристиками.