Треугольники можно классифицировать по различным характеристикам и свойствам, включая по видам углов. В зависимости от величины и типа углов, треугольники можно разделить на следующие категории:
1. Остроугольный треугольник
В остроугольном треугольнике все три угла являются острыми (меньше 90 градусов). Такой треугольник обладает острыми углами и острыми сторонами.
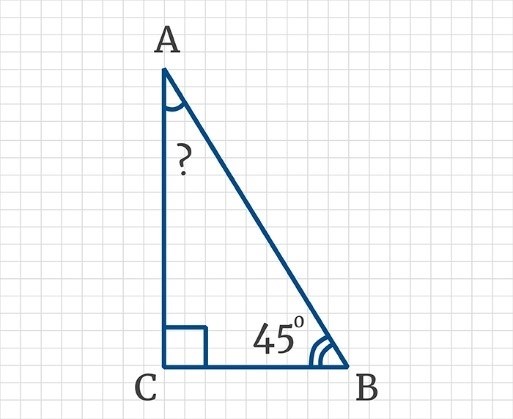
2. Прямоугольный треугольник
Прямоугольный треугольник имеет один прямой угол, который равен 90 градусов. Другие два угла в таком треугольнике являются острыми.
3. Тупоугольный треугольник
Тупоугольный треугольник характеризуется наличием одного тупого угла (больше 90 градусов) и двух острых углов.
4. Равнобедренный треугольник
В равнобедренном треугольнике две стороны равны между собой, а углы, противолежащие этим сторонам, также равны. Третий угол может быть остроугольным, прямоугольным или тупоугольным.
5. Равносторонний треугольник
Равносторонний треугольник имеет все три стороны равными между собой и все три угла равными.
6. Произвольный треугольник
Произвольный треугольник не имеет особых свойств по видам углов. Все три угла могут быть острыми, прямыми или тупыми в зависимости от их величины.
Теорема о сумме углов треугольника: Пояснение на примерах
Прямоугольный треугольник
Рассмотрим пример прямоугольного треугольника. В таком треугольнике один из углов равен 90 градусам. По теореме о сумме углов треугольника, сумма остальных двух углов должна быть равна 90 градусам. Например, угол α равен 30 градусам, а угол β равен 60 градусам. Тогда сумма углов треугольника будет равна 90 + 30 + 60 = 180 градусов.
Равносторонний треугольник
Равносторонний треугольник имеет все стороны и углы равными. Так как все углы равны в равностороннем треугольнике, значит каждый угол равен 60 градусам. Следовательно, сумма углов такого треугольника будет равна 60 + 60 + 60 = 180 градусов.
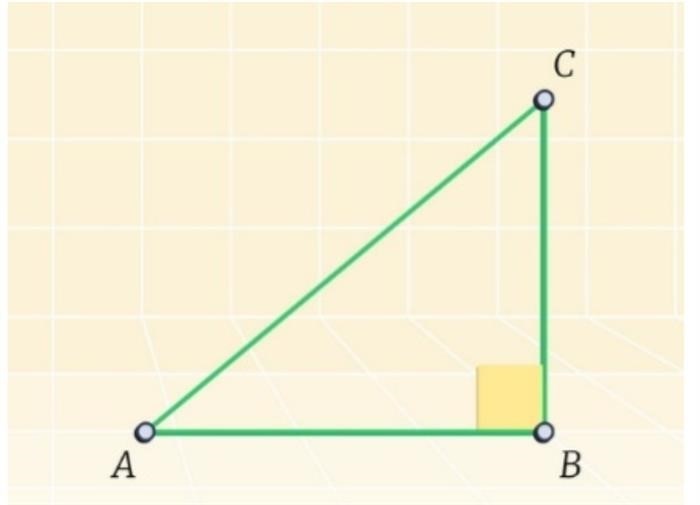
Произвольный треугольник
В произвольном треугольнике, где все углы могут быть разными, сумма углов также должна быть равна 180 градусов. Например, у треугольника ABC угол A равен 50 градусов, угол B равен 70 градусам, а угол C равен 60 градусам. Тогда сумма углов треугольника будет равна 50 + 70 + 60 = 180 градусов.
Таблица суммы углов
| Тип треугольника | Сумма углов |
|---|---|
| Прямоугольный треугольник | 180 градусов |
| Равносторонний треугольник | 180 градусов |
| Произвольный треугольник | 180 градусов |
Следствие из теоремы о сумме углов треугольника
1. Сумма углов в любом треугольнике равна 180 градусам
Следствие: Независимо от формы и размеров треугольника, сумма всех его внутренних углов всегда составляет 180 градусов.
2. Углы при основании равнобедренного треугольника равны
Следствие: Если у треугольника две равные стороны, то два угла при основании треугольника равны между собой. То есть, если две стороны треугольника равны, то два угла при основании будут равны.
3. Угол, противолежащий наибольшей стороне, самый большой
Следствие: В треугольнике угол, противолежащий наибольшей стороне, является самым большим. То есть, если в треугольнике одна сторона больше других двух, то угол, противолежащий этой стороне, будет больше остальных углов треугольника.
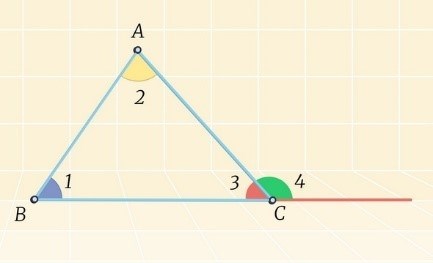
4. Сумма двух углов треугольника всегда больше третьего
Следствие: Внутренним углам треугольника можно поставить в соответствие длины его сторон. Сумма двух меньших углов всегда будет больше третьего угла. То есть, если в треугольнике сумма двух углов меньше третьего угла, то такой треугольник не может существовать.
Формулировка и формула теоремы
Теорема о сумме углов треугольника формулируется следующим образом: сумма всех внутренних углов треугольника равна 180 градусам.
Эта теорема является одной из самых основных в геометрии. Она позволяет нам легко вычислять величину недостающего угла треугольника или проверять правильность его построения. Благодаря этой теореме мы можем легко и с уверенностью работать с треугольниками в геометрических задачах.
Формула теоремы о сумме углов треугольника записывается следующим образом:
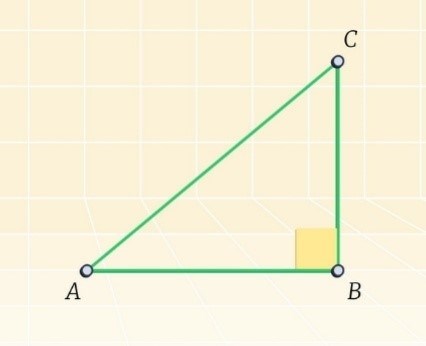
- Угол A: представлен точкой A, он расположен противоположно стороне BC.
- Угол B: представлен точкой B, он расположен противоположно стороне AC.
- Угол C: представлен точкой C, он расположен противоположно стороне AB.
Величина угла A обозначается как ∠A, угла B как ∠B и угла C как ∠C.
Теорема о сумме углов треугольника может быть записана в виде формулы:
∠A + ∠B + ∠C = 180°
Эта формула подтверждает, что сумма всех трех углов треугольника равна 180 градусам.
Итак, благодаря теореме о сумме углов треугольника, мы можем легко рассчитывать величину недостающего угла или проверять правильность построения треугольника. Формула этой теоремы ∠A + ∠B + ∠C = 180° служит основой для дальнейших вычислений и решения геометрических задач.