Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. Но есть также специальный случай, когда его диагонали пересекаются и делятся пополам. В этом случае каждая диагональ является осью симметрии фигуры, что делает ее параллелограммом. Такое свойство может быть полезным при решении геометрических задач или при классификации фигур.
Биссектриса в параллелограмме
Биссектриса в параллелограмме имеет следующие свойства:
- Биссектриса делит угол параллелограмма на два равных угла.
- Биссектриса проходит через точку пересечения диагоналей параллелограмма.
- Биссектриса является осью симметрии параллелограмма, так как все углы, образованные ею, являются равными.
- Биссектриса параллелограмма является отрезком, соединяющим середины противоположных сторон.
Биссектриса в параллелограмме играет важную роль при нахождении различных геометрических характеристик фигуры. Например, она позволяет определить точку пересечения диагоналей, которая является центром симметрии параллелограмма. Также биссектриса может использоваться для построения параллелограмма по заданным условиям.
| Свойство | Определение |
|---|---|
| Биссектриса угла | Отрезок, который делит угол пополам. |
| Биссектриса диагонали | Отрезок, который проходит через точку пересечения диагоналей и делит их на две равные части. |
Пример:
Пусть у нас есть параллелограмм ABCD, угол ABC равен 60 градусов. Найдем биссектрису этого угла.
Сначала найдем середину стороны AB, обозначим ее точкой M. Затем построим прямую, проходящую через точку M и делающую угол 30 градусов с прямой AB.
Точка пересечения прямой с стороной BC будет являться точкой пересечения биссектрисы с этой стороной.
Таким образом, мы нашли биссектрису угла ABC в параллелограмме ABCD.
Источник: www.math10.com
Всё о ромбе
Основные свойства ромба:
- Все стороны ромба равны
- Все углы ромба равны
- Диагонали ромба пересекаются в точке, деля ее пополам
Формула площади ромба:
Чтобы найти площадь ромба, нужно знать длины его диагоналей. Формула площади ромба выглядит следующим образом:
Площадь = (произведение длин диагоналей) / 2
Пример
Допустим, у нас есть ромб со стороной длиной 6 единиц и диагоналями равными 8 и 10 единиц. Чтобы найти его площадь, мы используем формулу:
Площадь = (8 * 10) / 2 = 40
Таким образом, площадь этого ромба равна 40 квадратным единицам.
Интересные факты о ромбе:
- Слово “ромб” происходит от греческого слова “rhombos”, что означает “четырехугольник со скругленными углами”.
- Ромб является основой для построения многих других геометрических фигур, таких как прямоугольник и квадрат.
- В природе много объектов, которые имеют форму ромба, например, лист клена или лепестки цветов.
| Тип четырехугольника | Свойства |
|---|---|
| Ромб | Все стороны равны Все углы равны Диагонали пересекаются и делятся пополам |
| Прямоугольник | Противоположные стороны равны Все углы прямые |
| Квадрат | Все стороны равны Все углы прямые |
| Параллелограмм | Противоположные стороны равны Противоположные углы равны |
Ромб – это уникальная геометрическая фигура, обладающая особыми свойствами. Его равные стороны и углы делают его основой для многих других фигур. Формула площади ромба позволяет вычислить его площадь на основе длин диагоналей. Интересные факты о ромбе добавляют ему уникальный характер и привлекательность.
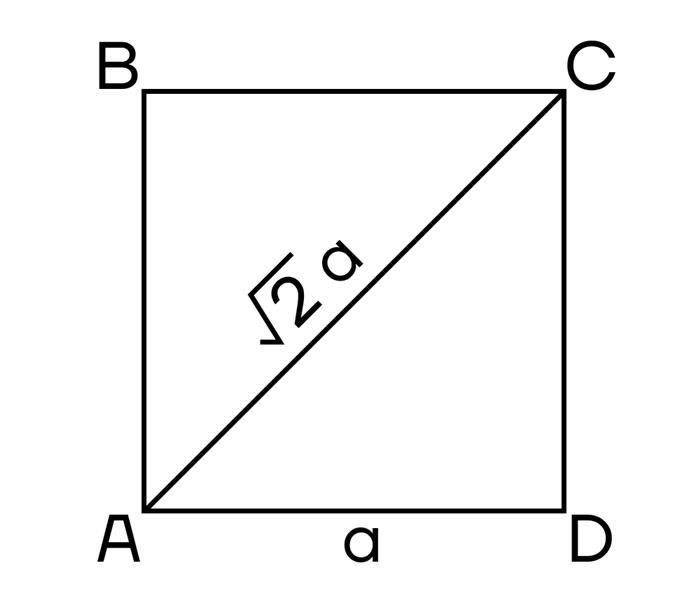
Всё о квадрате
Основные характеристики квадрата:
- У всех сторон одинаковая длина;
- Углы прямые (90 градусов);
- Диагонали равны и пересекаются в центре;
- Периметр квадрата равен сумме длин его сторон;
- Площадь квадрата равна квадрату длины его стороны.
| Свойство | Значение |
|---|---|
| Количество сторон | 4 |
| Углы | Прямые (90 градусов) |
| Диагонали | Равны и пересекаются в центре |
| Площадь | Длина стороны, возведенная в квадрат |
| Периметр | Сумма длин всех сторон |
Квадрат имеет множество свойств, которые делают его полезным в различных областях:
- В строительстве: квадратные формы легко объединяются, образуя фундаменты, стены и полы;
- В математике: квадрат используется для решения уравнений, моделирования графиков и пространственных преобразований;
- В дизайне: квадратные элементы интегрируются в различные объекты и создают сбалансированный и гармоничный вид;
- В планировании: квадратные участки земли используются для удобства и наилучшего использования пространства.
Биссектриса и площадь параллелограмма
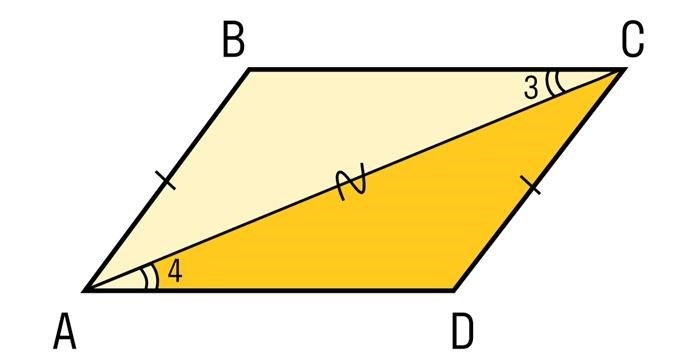
Биссектриса угла параллелограмма делит его на два равных треугольника. В обоих треугольниках биссектриса является медианой, а также высотой, опущенной на основание треугольника. Это значит, что площадь каждого треугольника можно вычислить по формуле: площадь = (основание * высота) / 2.
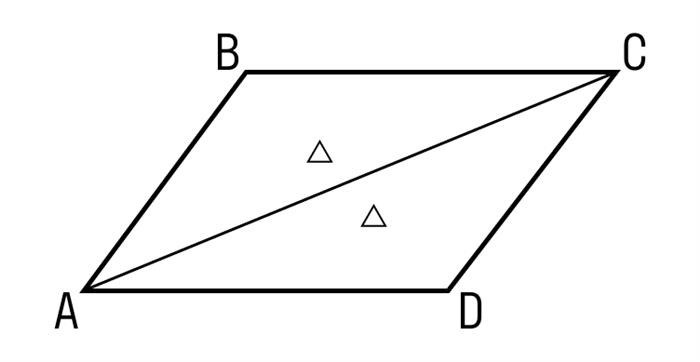
Так как основание у обоих треугольников одинаково, а высота равна половине длины диагонали параллелограмма, то их площади также будут равны между собой. Таким образом, площадь параллелограмма можно вычислить, умножив площадь одного треугольника на 2.
Итак, для параллелограмма, чьи диагонали пересекаются и делятся пополам, площадь равна удвоенной площади одного из его треугольников, а биссектриса является медианой и высотой треугольника, образованного одной из диагоналей.