Теорема косинусов и синусов для треугольника

Теорема косинусов и синусов – это основные математические формулы, используемые для нахождения сторон, углов и площади треугольника. Теорема косинусов позволяет найти сторону треугольника, зная длины двух других сторон и угол между ними, а теорема синусов позволяет найти отношения между сторонами и углами треугольника. Эти теоремы являются важными инструментами в геометрии и приложениях, связанных с треугольниками и их свойствами.

Формулировка и доказательство теоремы косинусов

Функция косинуса угла между двумя сторонами треугольника равна отношению квадрата длины третьей стороны к произведению длин двух других сторон, выраженному с обратным знаком. Математически это записывается следующим образом:

c² = a² + b² – 2abcosC

Где:

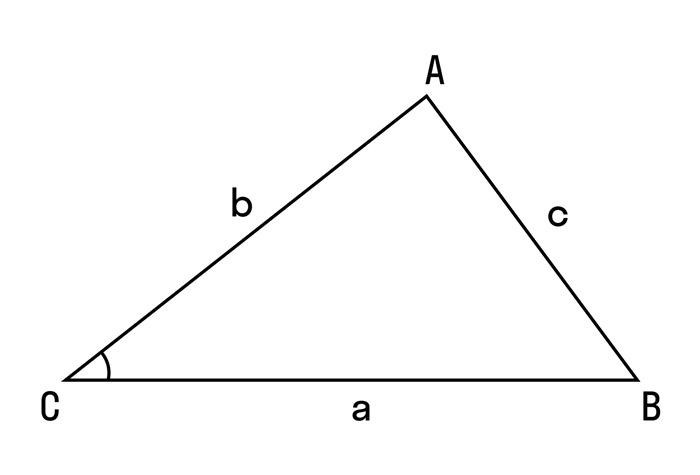
• c – длина стороны треугольника, противоположной углу C;
• a и b – длины двух других сторон;
• C – величина включенного угла.

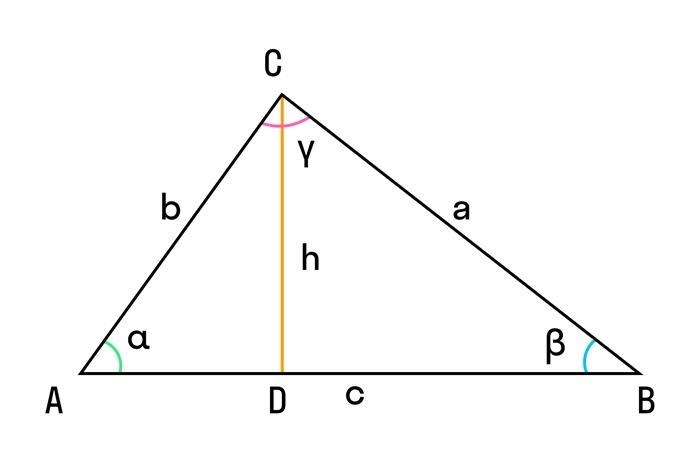
Используя теорему косинусов, можно найти длину любой стороны треугольника, если известны длины двух других сторон и величина включенного угла. Доказательство этой теоремы можно представить в виде следующей таблицы:

Величина	Обозначение	Доказательство
Высота	h	h = c * sin(A), где A – величина противоположного угла
Основание	b	b = c * cos(A), где A – величина противоположного угла
Синус угла	sin(A)	sin(A) = h / c
Косинус угла	cos(A)	cos(A) = b / c
Длина стороны треугольника	c	c = √(a2 + b2 – 2abcos(C)), где С – величина включенного угла

Таким образом, теорема косинусов позволяет вычислять длину сторон треугольника, основываясь на длинах других сторон и величине включенного угла. Это важное свойство, которое находит применение в геометрии, механике и других областях науки и техники.

Формулировка теорем для каждой из сторон треугольника

Теорема косинусов

Теорема косинусов позволяет найти длину одной из сторон треугольника, если известны длины двух других сторон и угол между этими сторонами.

1. Для стороны a:

a² = b² + c² – 2bc * cos(A)

где a – искомая сторона, b и c – известные стороны треугольника, A – угол между сторонами b и c.

2. Для стороны b:

b² = a² + c² – 2ac * cos(B)

где b – искомая сторона, a и c – известные стороны треугольника, B – угол между сторонами a и c.

3. Для стороны c:

c² = a² + b² – 2ab * cos(C)

где c – искомая сторона, a и b – известные стороны треугольника, C – угол между сторонами a и b.

Теорема синусов

Теорема синусов позволяет найти длину одной из сторон треугольника, если известны длины двух других сторон и соответствующие противолежащие им углы.

1. Для стороны a:

a / sin(A) = b / sin(B) = c / sin(C)

где a – искомая сторона, A – угол противолежащий стороне a, b – известная сторона, B – угол противолежащий стороне b, c – известная сторона, C – угол противолежащий стороне c.

2. Для стороны b:

b / sin(B) = a / sin(A) = c / sin(C)

где b – искомая сторона, B – угол противолежащий стороне b, a – известная сторона, A – угол противолежащий стороне a, c – известная сторона, C – угол противолежащий стороне c.

3. Для стороны c:

c / sin(C) = a / sin(A) = b / sin(B)

где c – искомая сторона, C – угол противолежащий стороне c, a – известная сторона, A – угол противолежащий стороне a, b – известная сторона, B – угол противолежащий стороне b.

Средняя линия треугольника

Свойства средней линии треугольника:

• Средняя линия равна половине длины соответствующей стороны треугольника;
• Все три средние линии пересекаются в одной точке – точке пересечения медиан;
• Средняя линия параллельна третьей стороне треугольника;
• Если провести все три средние линии треугольника, они разделят треугольник на шесть меньших треугольников, каждый из которых будет иметь одну из средних линий в качестве стороны.

Средняя линия треугольника может использоваться для решения различных геометрических задач, как например:

1. Нахождение площади треугольника. Площадь треугольника можно вычислить, используя длину средней линии и одну из сторон треугольника;
2. Построение вписанного в треугольник круга. Радиус вписанного круга будет равен половине длины средней линии треугольника;
3. Доказательство параллельности сторон треугольника. Если средняя линия параллельна одной из сторон, то она также будет параллельна другой стороне треугольника;
4. Построение центра тяжести треугольника. Центр тяжести треугольника – это точка пересечения средних линий треугольника.

Цитата: “Средняя линия треугольника является важным инструментом изучения геометрии и используется в решении различных задач, связанных с треугольниками.”

Таблица:

Свойство	Формула
Длина средней линии	Половина длины соответствующей стороны
Точка пересечения медиан	Общая точка пересечения всех средних линий
Параллельность	Средняя линия параллельна третьей стороне треугольника

Вершины, углы и стороны треугольника

Вершины треугольника

Вершины треугольника – это точки, где стороны пересекаются. Треугольник имеет три вершины, которые обозначаются буквами A, B и C. Например, если треугольник обозначен как ABC, то A, B и C – это его вершины.

Углы треугольника

Углы треугольника образуются между сторонами и могут быть различного размера. В треугольнике есть три угла, которые обозначаются буквами A, B и C, соответственно. Углы могут быть острыми, прямыми или тупыми, в зависимости от их размера. Например, если угол между сторонами AB и AC обозначен как BAC, то BAC – это угол треугольника ABC.

Стороны треугольника

Стороны треугольника – это отрезки, которые соединяют вершины треугольника. В треугольнике есть три стороны, которые обозначаются буквами a, b и c, соответственно. Например, сторона между вершинами A и B обозначается как AB.

• Периметр треугольника – сумма длин всех трех сторон.
• Остроугольный треугольник – треугольник, все углы которого острые.
• Прямоугольный треугольник – треугольник, один из углов которого прямой (равен 90 градусам).
• Тупоугольный треугольник – треугольник, один из углов которого тупой (больше 90 градусов).
• Равносторонний треугольник – треугольник, все стороны которого равны.
• Равнобедренный треугольник – треугольник, у которого две стороны равны.

Связь между сторонами и углами треугольника

В треугольнике существуют теоремы, которые описывают связь между сторонами и углами.

Теорема косинусов

Теорема косинусов гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон, умноженных на два произведения этих сторон на косинус угла между ними. Математически это выглядит следующим образом:

c² = a² + b² – 2ab * cos(C)

Теорема синусов

Теорема синусов гласит, что отношение синуса угла к длине противоположной стороны постоянно для всех углов треугольника. Математически это выглядит следующим образом:

sin(A)/a = sin(B)/b = sin(C)/c

Теоремы косинусов и синусов позволяют находить неизвестные стороны и углы треугольника, используя известные значения. Они являются важными инструментами в геометрии и находят применение в различных областях, включая инженерные расчеты и навигацию.

Формулы площади треугольника

Формула полупериметра

Полупериметр треугольника – это половина суммы длин его сторон. Формула полупериметра может быть использована для вычисления площади треугольника в сочетании с радиусом вписанной окружности. Формула выглядит следующим образом:

S = P * r

где S – площадь треугольника, P – полупериметр треугольника, r – радиус вписанной окружности.

Формула Герона

Формула Герона – это один из методов вычисления площади треугольника с использованием длин его сторон. Формула Герона основана на полупериметре треугольника и его сторонах и выглядит следующим образом:

S = √(p * (p-a) * (p-b) * (p-c))

где S – площадь треугольника, p – полупериметр треугольника, a, b, c – длины его сторон.

Формула синуса

Формула синуса позволяет вычислить площадь треугольника с использованием длин сторон треугольника и синуса угла между ними. Формула синуса выглядит следующим образом:

S = (a * b * sin(C)) / 2

где S – площадь треугольника, a и b – длины его сторон, C – угол между этими сторонами.

Формула косинуса

Формула косинуса также позволяет вычислить площадь треугольника с использованием длин его сторон и косинуса одного из его углов. Формула косинуса выглядит следующим образом:

S = (a 2 * b 2 * sin(C)) / (2 * c)

где S – площадь треугольника, a, b и c – длины его сторон, C – угол между сторонами a и b.

Примеры использования формул

• Если известны длины сторон треугольника и угол между ними, можно использовать формулу синуса для вычисления площади.
• Если известны длины всех сторон треугольника, можно использовать формулу Герона для вычисления площади.
• Если известны длины двух сторон и угол между ними, можно использовать формулу косинуса для вычисления площади.
• Если известны длины сторон треугольника и радиус вписанной окружности, можно использовать формулу полупериметра для вычисления площади.

Готовьтесь к экзамену вместе с образовательным порталом «Школково»

На пути к успешной сдаче экзамена важно подготовиться должным образом. Образовательный портал «Школково» предлагает вам уникальную возможность глубокого изучения темы “Теорема косинусов и синусов для треугольника”.

Изучайте удобно

Образовательный портал «Школково» предлагает гибкий формат обучения, который позволит вам изучать материал в удобное для вас время и место. Вы можете изучать теорию и решать практические задания как дома, так и в школе, в зависимости от ваших предпочтений и возможностей.

Глубокое понимание темы

Образовательный портал «Школково» поможет вам не только запомнить формулы и правила, но и понять их глубинный смысл. Вы сможете разобраться, как применять теорему косинусов и синусов для решения разнообразных задач и применять их в практической деятельности.

Интерактивные задания и тесты

На образовательном портале «Школково» вы найдете большое количество интерактивных заданий и тестов, которые помогут вам закрепить пройденный материал. Вы сможете самостоятельно проверить свои знания и навыки, а также отследить свой прогресс в обучении.

Учитеся вместе с экспертами

На образовательном портале «Школково» вы сможете общаться с опытными преподавателями и другими учениками, делиться опытом и задавать вопросы по теме “Теорема косинусов и синусов для треугольника”. Вы получите профессиональную поддержку и сможете разрешить возникшие вопросы.

Воспользуйтесь преимуществами образовательного портала «Школково»

Разнообразные формы обучения, глубокое понимание темы, интерактивные задания, возможность общения с экспертами – все это преимущества, которые помогут вам успешно подготовиться к экзамену по теме “Теорема косинусов и синусов для треугольника” вместе с образовательным порталом «Школково».

Определение угла с помощью косинуса

Данная теорема формулируется следующим образом: в треугольнике сторона, возведенная в квадрат, равна сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.

Таким образом, косинус можно использовать для определения угла треугольника, если известны длины сторон треугольника. Для этого необходимо воспользоваться обратной функцией косинуса, которая называется арккосинусом или cos^-1. Например, если известны длины сторон треугольника a, b и c, а требуется найти угол C, то можно использовать следующую формулу:

• Cos^-1((a² + b² – c²) / (2ab)) = C

Полученное значение будет выражать угол C в радианах. Чтобы перевести его в градусы, необходимо умножить значение на 180 и разделить на π (пи).

Зная значение угла треугольника, можно использовать геометрические свойства, чтобы находить различные параметры треугольника, решать задачи на поиск неизвестных сторон и углов.

Пример вычисления угла с использованием косинуса:

Пусть у нас есть треугольник ABC, в котором известны длины сторон: AB = 5, BC = 8 и AC = 10. Найдем угол A.

Используем формулу:

• Cos^-1((BC² + AC² – AB²) / (2 * BC * AC)) = A
• Cos^-1((8² + 10² – 5²) / (2 * 8 * 10)) = A
• Cos^-1(144 / 160) = A
• Примерно A = 0.7227 радиан

Переведем значение угла A в градусы:

• (0.7227 * 180) / π ≈ 41.42 градусов

Таким образом, угол A треугольника ABC равен примерно 41.42 градусов.

Рассмотрение пределов изменения cos α и sin α

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nullam aliquet ultrices ligula, vitae iaculis nibh imperdiet vel. Nulla non leo rutrum, efficitur nisi ut, congue ligula. Nullam auctor, ipsum in placerat efficitur, mauris risus aliquam lacus, at finibus ligula risus in augue. Fusce sit amet nibh convallis, consequat felis non, sodales mi. Sed non turpis vitae ipsum consequat lacinia nec sed nisi. Nunc et tellus sed lacus rutrum efficitur sed ut leo. Nullam nec purus dignissim, fringilla felis sed, tempor dolor. Nullam congue volutpat felis, eu laoreet justo suscipit ac. Sed vitae efficitur augue, ac maximus enim.

Vestibulum id ipsum ac leo ultrices mollis sit amet sit amet ex. Praesent fringilla nunc in dui vulputate, eget tincidunt lectus cursus. Nam at lacinia nunc. Aliquam sollicitudin quam dolor, non ullamcorper leo pharetra a. Nullam hendrerit orci vitae urna congue mattis. Mauris consequat, lacus non ultricies facilisis, mi lacus eleifend purus, nec blandit purus nisi vitae enim. Quisque dignissim, enim id suscipit tincidunt, velit justo lacinia neque, sit amet efficitur risus elit auctor enim. Nam a felis eu risus semper sollicitudin in sed diam. Sed dictum magna quis velit placerat, nec malesuada est consequat. Vivamus sed justo bibendum, convallis nulla sit amet, feugiat ligula. Curabitur nec pretium metus. Sed faucibus erat id dui finibus, xe quis egestas metus.

Таблица: Значения cos α и sin α

Угол α	cos α	sin α
0	1	0
π/6	√3/2	1/2
π/4	√2/2	√2/2
π/3	1/2	√3/2
π/2	0	1

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut pharetra sed sapien a consectetur. Donec scelerisque sagittis varius. Nunc ultrices lorem in mi feugiat, non rutrum orci eleifend. Fusce laoreet risus quis bibendum egestas. Duis lacinia urna justo. Sed posuere posuere metus, vel ultrices justo finibus ac. Integer rhoncus, mi nec condimentum venenatis, nulla arcu finibus magna, vitae dignissim ligula eros non purus. Aliquam pharetra arcu quam, vel ornare lectus commodo a. Ut bibendum metus ultrices, sodales nunc eget, bibendum mauris.

Формулы и доказательства для нахождения угла в треугольнике

В геометрии существует несколько формул и методов, которые помогают найти угол в треугольнике. Рассмотрим некоторые из них:

1. Теорема косинусов

Теорема косинусов гласит, что квадрат одной стороны треугольника равен сумме квадратов двух других сторон, умноженных на два произведения этих сторон и косинус угла между ними. Формула для нахождения угла α в треугольнике по теореме косинусов имеет вид:

cos(α) = (b² + c² – a²) / (2bc)

Где a, b и c – длины сторон треугольника.

2. Теорема синусов

Теорема синусов устанавливает соотношение между сторонами и углами в треугольнике. Формула для нахождения угла α в треугольнике по теореме синусов имеет вид:

sin(α) = (a / c) * sin(γ)

Где a и c – стороны треугольника, а γ – противолежащий угол.

Доказательство формулы для нахождения угла по теореме косинусов:

Предположим, что у нас есть треугольник ABC с известными длинами сторон a, b и c. Нам нужно найти угол α, противолежащий стороне a.

1. Обозначим угол α как угол между сторонами b и c.
2. Используя закон косинусов, запишем следующее равенство: a² = b² + c² – 2bc * cos(α).
3. Разрешим уравнение относительно cos(α): cos(α) = (b² + c² – a²) / (2bc).
4. Находим значение cos(α).
5. Используя тригонометрическую функцию арккосинус, найдем значение угла α: α = arccos[(b² + c² – a²) / (2bc)].

Применение формул и доказательство для нахождения угла

Формулы, такие как теорема косинусов и теорема синусов, являются полезными инструментами при решении геометрических задач. Они позволяют найти неизвестные углы в треугольнике на основе известных данных о его сторонах. Доказательство формулы для нахождения угла по теореме косинусов позволяет увидеть связь между углом и длинами сторон треугольника.

Теорема	Формула
Теорема косинусов	cos(α) = (b² + c² – a²) / (2bc)
Теорема синусов	sin(α) = (a / c) * sin(γ)

Используя эти формулы, можно с легкостью находить углы в треугольнике и решать сложные задачи, связанные с геометрией.

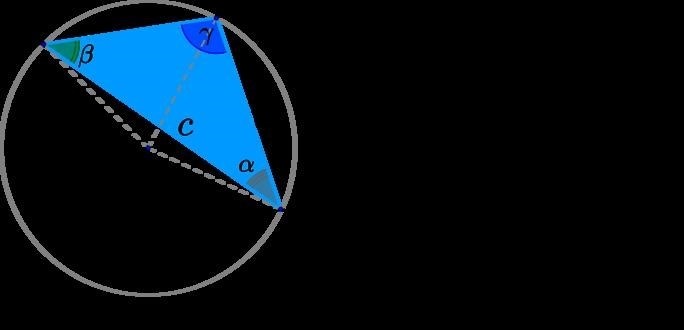
Связь между вписанной и описанной окружностями треугольника

Вписанная и описанная окружности треугольника тесно связаны между собой и имеют множество свойств, которые можно использовать для решения различных задач.

Вписанная окружность – это окружность, которая касается всех сторон треугольника внутренним образом. Вписанная окружность имеет центр, который совпадает с центром вписанного в треугольник круга, называемого инкругом. Радиус вписанной окружности равен полупериметру треугольника, разделенному на сумму длин его сторон:

r = (a + b + c) / 2s, где r – радиус вписанной окружности, a, b, c – стороны треугольника, s – полупериметр.

Описанная окружность – это окружность, которая проходит через все вершины треугольника. Описанная окружность имеет центр, который совпадает с центром описанного около треугольника круга, называемого описанным около треугольника кругом. Радиус описанной окружности равен половине произведения сторон треугольника, деленному на его полупериметр:

R = abc / 4Sr, где R – радиус описанной окружности.

Инициализация связи между вписанной и описанной окружностями треугольника позволяет применять теорему секущих и теорему о вписанных углах для нахождения различных величин и свойств треугольника.

Также, будучи важными геометрическими объектами, вписанная и описанная окружности треугольника используются для построения различных геометрических конструкций и решения задач в различных областях науки и техники.