Четырехугольник вписан в окружность, если все его вершины лежат на окружности, а его диагонали пересекаются в центре окружности.
Формулы и соотношения для четырехугольника, вписанного в окружность
Четырехугольник, вписанный в окружность, имеет ряд интересных свойств и соотношений, которые можно выразить математическими формулами. Эти формулы позволяют вычислять различные параметры и связи между сторонами и углами четырехугольника.
Ниже приведены некоторые из основных формул и соотношений для четырехугольника, вписанного в окружность:
1. Формула для площади четырехугольника:
Площадь четырехугольника, вписанного в окружность, можно вычислить по формуле:

S = (r/2) * (a + b + c + d)
где S – площадь четырехугольника, r – радиус окружности, a, b, c и d – длины сторон четырехугольника.
2. Соотношение между противоположными углами:
Противоположные углы четырехугольника, вписанного в окружность, сумма которых равна 180°. Формула для вычисления одного из противоположных углов:
Угол АВС + Угол СDА = 180°
3. Соотношение между сторонами и радиусом окружности:
Для четырехугольника, вписанного в окружность, справедливо следующее соотношение между сторонами и радиусом окружности:
a * b * c * d = r 4
где a, b, c и d – длины сторон четырехугольника, r – радиус окружности.
4. Соотношение между радиусом окружности и углами четырехугольника:
Для четырехугольника, вписанного в окружность, справедливо следующее соотношение между радиусом окружности и углами:
- Угол АВС/2 = α/2 = β (половина центрального угла АС)
- Угол ACD/2 = γ/2 = δ (половина центрального угла CD)
5. Соотношение между сторонами и углами четырехугольника:
Для четырехугольника, вписанного в окружность, справедливо соотношение между сторонами и углами:
a * sin(α) = b * sin(β) = c * sin(γ) = d * sin(δ)

где a, b, c и d – длины сторон четырехугольника, α, β, γ и δ – углы четырехугольника.
| Формула/Соотношение | Описание |
|---|---|
| S = (r/2) * (a + b + c + d) | Площадь четырехугольника |
| Угол АВС + Угол СDА = 180° | Соотношение между противоположными углами |
| a * b * c * d = r 4 | Соотношение между сторонами и радиусом окружности |
| Угол АВС/2 = α/2 = β Угол ACD/2 = γ/2 = δ |
Соотношение между радиусом окружности и углами |
| a * sin(α) = b * sin(β) = c * sin(γ) = d * sin(δ) | Соотношение между сторонами и углами |
Формулы и соотношения для четырехугольника, вписанного в окружность, позволяют расширить наши знания о свойствах этой геометрической фигуры и использовать их для решения различных задач.
Как найти радиус вписанного в окружность четырехугольника, формула
Вписанный в окружность четырехугольник обладает рядом особенностей, включая равенство суммы противоположных углов, равенство противоположных сторон и особую связь между радиусом окружности и сторонами четырехугольника. Чтобы найти радиус вписанной окружности, нужно использовать специальную формулу, основанную на связи между радиусом и сторонами четырехугольника.
Формула для нахождения радиуса вписанной окружности
Существует формула, позволяющая найти радиус вписанной окружности в зависимости от длин сторон четырехугольника. Для этого нужно знать длины всех сторон четырехугольника и применить следующую формулу:
r = sqrt{frac{(a + b + c + d)(-a + b + c + d)(a – b + c + d)(a + b – c + d)}{(4s) 2}}
| Обозначение | Значение |
|---|---|
| r | Радиус вписанной окружности |
| a, b, c, d | Длины сторон четырехугольника |
| s | Полупериметр четырехугольника (s = (a + b + c + d) / 2) |
Обратите внимание, что в формуле длины сторон четырехугольника а, b, c, d должны быть выражены в одной и той же единице измерения.
Таким образом, зная длины сторон четырехугольника, вы можете легко найти радиус вписанной окружности, применяя указанную формулу. Это позволит вам более точно изучить свойства и особенности данного четырехугольника и использовать полученные значения для решения задач и вычислений, связанных с ним.
Чему равна сумма противоположных углов вписанного в окружность четырехугольника
Во вписанном в окружность четырехугольнике сумма противоположных углов оказывается равной 180 градусам. Такое свойство можно объяснить с помощью нескольких ключевых факторов и формул геометрии.
Формулы геометрии для подтверждения свойства
- Углы в окружности – наполовину вписанные углы, поэтому каждый угол, вписанный в окружность, будет составлять половину соответствующего ему центрального угла.
- Сумма центральных углов в окружности составляет 360 градусов.
- Если разделить каждый центральный угол на два, получим вписанный угол, который равен половине центрального угла.
Доказательство равенства суммы углов
Предположим, у нас есть четырехугольник ABCD, который вписан в окружность. Углы A и C являются противоположными, а углы B и D также считаются противоположными. Для доказательства окажется достаточно показать, что сумма углов A и C равна сумме углов B и D, то есть задача сводится к равенству двух пар противоположных углов.
Исходя из формул геометрии, каждый противоположный угол в четырехугольнике вписанный в окружность равен половине соответствующего центрального угла, который составляет 180 градусов. Поскольку центральные углы в окружности дают в сумме 360 градусов, их половины будут равны 180 градусам.
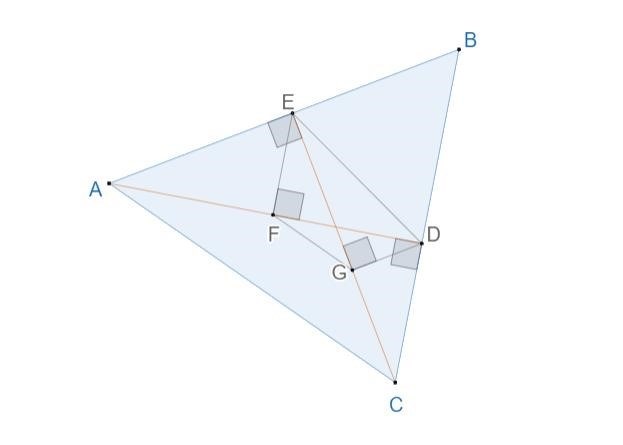
Другими словами, A/2 + C/2 = 180 градусов и B/2 + D/2 = 180 градусов. Если сложить эти уравнения, то получим:
A/2 + C/2 + B/2 + D/2 = 360 градусов
Упростив уравнение, получим:
(A + C + B + D)/2 = 360 градусов
Так как сумма углов A + C + B + D в четырехугольнике равна 360 градусам, мы можем утверждать, что их половина, то есть сумма противоположных углов A и C, равна 180 градусам.
Площадь четырехугольника и вписанная окружность: связь через формулу
Давайте разберемся подробнее, как эта формула работает.
Формула для вычисления площади четырехугольника вписанного в окружность:
-
Найдем длины сторон четырехугольника.
Для этого можно использовать теорему косинусов или теорему Пифагора в зависимости от типа четырехугольника.
-
Найдем полупериметр четырехугольника.
Полупериметр вычисляется, как сумма всех сторон, поделенная на 2.
-
Найдем радиус вписанной окружности.
Формула для вычисления радиуса вписанной окружности может быть разной в зависимости от типа четырехугольника, но в общем случае она может быть записана следующим образом:
r = sqrt(((s-a)(s-b)(s-c)(s-d)) / ((s-a)+(s-b)+(s-c)+(s-d))),где r – радиус, s – полупериметр четырехугольника, a, b, c, d – стороны четырехугольника.
-
Используем радиус для вычисления площади.
Формула для вычисления площади может быть разной в зависимости от типа четырехугольника, но в общем случае она может быть записана следующим образом:
S = r * (s-a) * (s-b) * (s-c) * (s-d),где S – площадь, r – радиус, s – полупериметр четырехугольника, a, b, c, d – стороны четырехугольника.
Итак, площадь четырехугольника вписанного в окружность и радиус вписанной окружности связаны между собой формулой. Зная радиус, мы можем найти площадь, а зная площадь, можем вычислить радиус. Эта формула удобна для установления связи между двумя основными характеристиками четырехугольника и может быть использована для решения различных задач в геометрии.
Вписанный четырехугольник – определения и теоремы
Основные свойства вписанного четырехугольника:
- Углы противолежащих сторон: Сумма углов, противолежащих сторонам, равна 180 градусам.
- Сумма углов: Сумма всех внутренних углов вписанного четырехугольника также равна 360 градусам.
- Диаметры: Хорда, соединяющая середины противоположных сторон, является диаметром окружности.
- Углы, опирающиеся на одну дугу: Углы, опирающиеся на одну дугу окружности, равны между собой.
- Угол между хордами: Угол между двумя хордами, пересекающимися внутри окружности, равен половине суммы углов, образованных этими хордами на окружности.
Вписанный четырехугольник является интересным объектом изучения и на нем основано множество теорем и свойств. Одной из важных теорем является Теорема о вписанном угле, которая гласит:
Вписанный угол, опирающийся на окружность, равен половине центрального угла, опирающегося на ту же дугу.
Существуют также другие теоремы, связанные с геометрическими свойствами вписанных четырехугольников. Они играют важную роль в решении задач и построении фигур.
Вписанные четырехугольники являются одной из основных тем геометрии и находят применение в различных областях, таких как архитектура, инженерное дело и компьютерная графика.
Вписанный четырехугольник – коротко о главном
В данной статье мы рассмотрели свойства четырехугольника, который описывает окружность.
Вписанный четырехугольник обладает рядом интересных и полезных свойств.
1. Вписанный угол: внутри такого четырехугольника существует особый угол – вписанный угол. Он равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол. Вписанный угол имеет большое значение в различных геометрических и тригонометрических задачах.
2. Сумма противолежащих углов: сумма противолежащих углов в вписанном четырехугольнике всегда равна 180 градусов. Это свойство обусловлено тем, что все вершины лежат на окружности, а сумма углов, опирающихся на ту же дугу, равна 180 градусов.
3. Формула для нахождения площади: для вписанного четырехугольника существует специальная формула для нахождения его площади. Она зависит от радиуса окружности и длин сторон четырехугольника.
- Для треугольника вписанного в окружность существует формула: площадь = (полупериметр * радиус окружности).
- Для четырехугольника, состоящего из двух таких треугольников, площадь можно вычислить с помощью формулы: площадь = (площадь первого треугольника + площадь второго треугольника).
Итак, вписанный четырехугольник имеет ряд характерных свойств, которые можно использовать при решении геометрических задач. Знание этих свойств позволяет более глубоко понять и изучить взаимосвязь геометрических фигур.