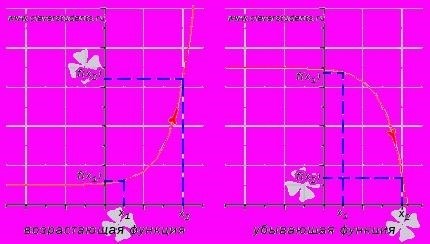
Промежутки возрастания и убывания функции – это интервалы на оси абсцисс, где функция возрастает или убывает. Возрастание функции характеризуется увеличением значений функции с увеличением значения аргумента, тогда как убывание функции – уменьшением значений функции с увеличением значения аргумента. Расчет промежутков возрастания и убывания функции основан на производной функции и ее знаке. Отличное понимание этих концепций позволяет более глубоко изучать поведение функций и решать задачи математического анализа.
Достаточные условия возрастания и убывания функции
1. Первая производная функции
Одним из основных достаточных условий возрастания и убывания функции является анализ ее первой производной. Если производная положительна на некотором промежутке, то функция возрастает на этом промежутке. Если же производная отрицательна, то функция убывает на данном промежутке.
2. Вторая производная функции
Вторая производная функции также играет важную роль в определении возрастания и убывания. Если вторая производная положительна на некотором промежутке, то функция выпукла вверх на этом промежутке и возрастает. Если же вторая производная отрицательна, то функция выпукла вниз и убывает на данном промежутке.
3. Критические точки
Кроме производных, важными являются также критические точки функции, которые определяются как ее точки, где первая производная равна нулю или не существует. Возрастание и убывание функции на отрезке зависит от того, как меняется знак первой производной в окрестности критической точки.
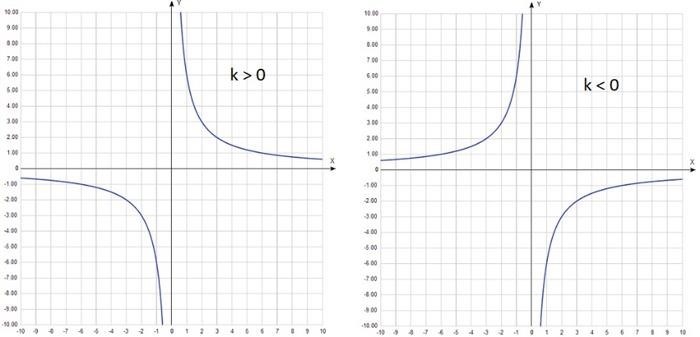
4. Точки экстремума
Точки экстремума функции, которые определяются как точки, где первая производная меняет знак с положительного на отрицательный или наоборот, также являются важными при анализе возрастания и убывания функции. Если первая производная меняет знак от плюса к минусу, то функция достигает максимума. Если знак меняется от минуса к плюсу, то функция достигает минимума.
5. Таблица условий возрастания и убывания функции
| Промежуток | Условия возрастания | Условия убывания |
|---|---|---|
| Производная положительна | + | |
| Производная отрицательна | – | |
| Вторая производная положительна | ↑ | |
| Вторая производная отрицательна | ↓ |
Примечание: Знак “+” указывает на возрастание функции, знак “-” указывает на убывание функции, стрелки “↑” и “↓” указывают на выпуклость вверх и вниз соответственно.
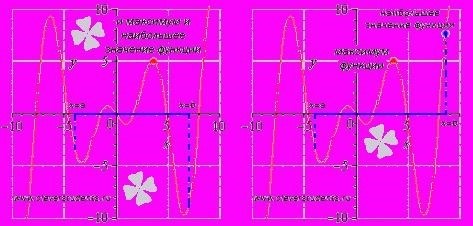
Что такое убывание функции
Строгое убывание функции
- Функция называется строго убывающей на интервале, если для любых двух различных аргументов этого интервала значение функции при первом аргументе будет меньше значения функции при втором аргументе.
- По определению, если производная функции на интервале отрицательна, то функция строго убывает на этом интервале.
- На графике функции строгое убывание проявляется снижением функции по направлению оси абсцисс.
Нестрогое убывание функции
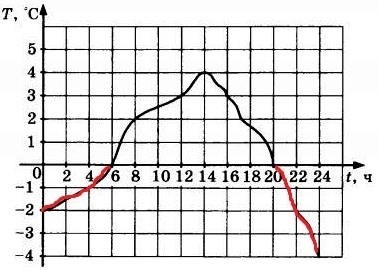
- Функция называется нестрого убывающей на интервале, если для любых двух различных аргументов этого интервала значение функции при первом аргументе будет меньше или равно значению функции при втором аргументе.
- Функция может быть нестрого убывающей, даже если ее производная на интервале неотрицательна.
- На графике функции нестрогое убывание проявляется в установлении горизонтальной или наклонной прямой, которая не опускается.
Таким образом, убывание функции важно для определения поведения функции и ее графика. При анализе функции, необходимо учитывать, как аргументы влияют на значения функции и как меняется функция в зависимости от изменения аргумента.
Точки экстремума, экстремумы функции
В данной статье мы рассмотрели промежутки возрастания и убывания функции, а также способы нахождения и классификации экстремумов функции.
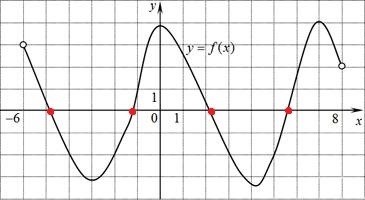
Основная задача при изучении точек экстремума и экстремумов функции заключается в определении максимального (минимального) значения функции на заданном отрезке или в заданной области. Для этого проводится анализ производной функции и её поведения в окрестности критических точек.
В результате исследования функции и определения точек экстремума можно получить полную информацию о форме и поведении функции. Это позволяет оптимизировать работу с функцией, применять её в решении различных задач и изучении разных явлений.