Уравнение касательной к графику функции позволяет определить угловой коэффициент этой касательной и точку ее касания с графиком функции. Касательная является прямой, которая касается графика функции в определенной точке и имеет такой же наклон, как и график функции в этой точке.
Для составления уравнения касательной к графику функции нужно знать координаты точки касания и значение производной функции в этой точке. Пусть у нас есть функция y = f(x) и точка касания (a, f(a)). Тогда уравнение касательной будет иметь вид:
y – f(a) = f'(a)(x – a)
Здесь f'(a) – значение производной функции f(x) в точке (a, f(a)). Это значение можно найти путем дифференцирования функции f(x). Для этого нужно найти производную функции и подставить в нее точку (a, f(a)).
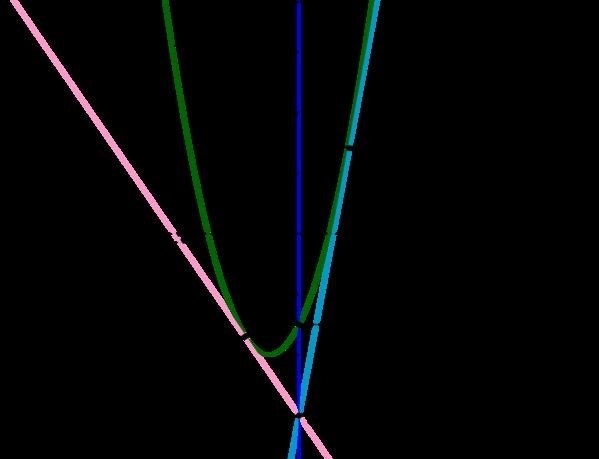
В результате получаем уравнение касательной, которое позволяет определить наклон касательной и точку ее касания с графиком функции. Это уравнение представляет собой линейную функцию и позволяет аппроксимировать график функции вблизи точки касания.
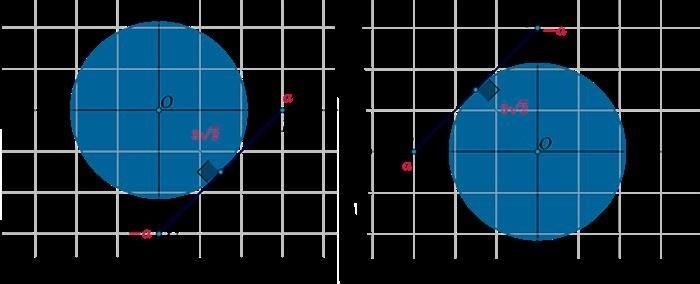
Как получить уравнение касательной и уравнение нормали
Уравнение касательной к графику функции
Уравнение касательной к графику функции в определенной точке позволяет найти наклон касательной и точку пересечения с осью абсцисс. Для получения уравнения касательной, следует выполнить следующие шаги:
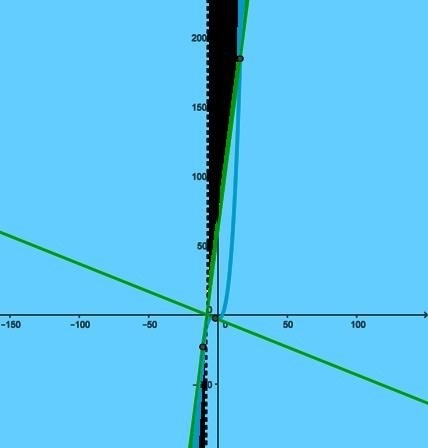
- Найти производную функции.
- Подставить в производную значение аргумента, соответствующее точке, в которой требуется найти касательную.
- Полученное значение является наклоном касательной.
- Найти координаты точки, в которой требуется найти касательную.
- Подставить полученные значения в уравнение прямой вида y = kx + b, где k – наклон касательной, а b – коэффициент сдвига.
Уравнение нормали к графику функции
Уравнение нормали к графику функции в определенной точке позволяет найти наклон нормали и точку пересечения с осью абсцисс. Чтобы получить уравнение нормали, следует выполнить аналогичные шаги, как при нахождении уравнения касательной, но с использованием обратного значения наклона.
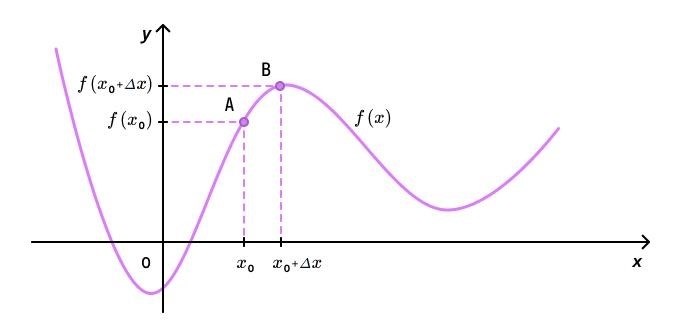
Итог
Получение уравнений касательной и нормали позволяет анализировать поведение функции в конкретных точках. Знание наклона касательной и нормали позволяет определить возрастание или убывание функции в данной точке, а также ее поведение на всем графике. Эта информация важна при решении задач из различных областей науки и инженерии.
