Расстояние от точки до прямой – это одна из основных задач аналитической геометрии. Оно является мерой отклонения точки от прямой и находит применение во многих областях, таких как физика, компьютерная графика и оптимизация. Рассмотрим координатный метод, который позволяет найти расстояние между точкой и прямой на плоскости при помощи формулы, основанной на использовании координат точки и уравнения прямой.
Какой метод использовать для вычисления расстояния от точки до прямой?
При необходимости вычисления расстояния от точки до прямой можно воспользоваться различными методами, каждый из которых имеет свои особенности и преимущества. Выбор оптимального метода зависит от конкретной задачи и доступных данных.
1. Геометрический метод
Геометрический метод основан на построении геометрической модели задачи и использовании геометрических свойств. Данный метод позволяет наглядно представить ситуацию и является простым в использовании, однако требует достаточного уровня геометрической подготовки. Для применения данного метода необходимо знать уравнение прямой и координаты точки.
2. Формульный метод
Формульный метод основан на использовании алгебраических формул для вычислений. Данный метод является более универсальным, поскольку не требует непосредственного построения геометрической модели и может быть использован в случае любых формул и уравнений. Для применения данного метода необходимо знать уравнение прямой и координаты точки.
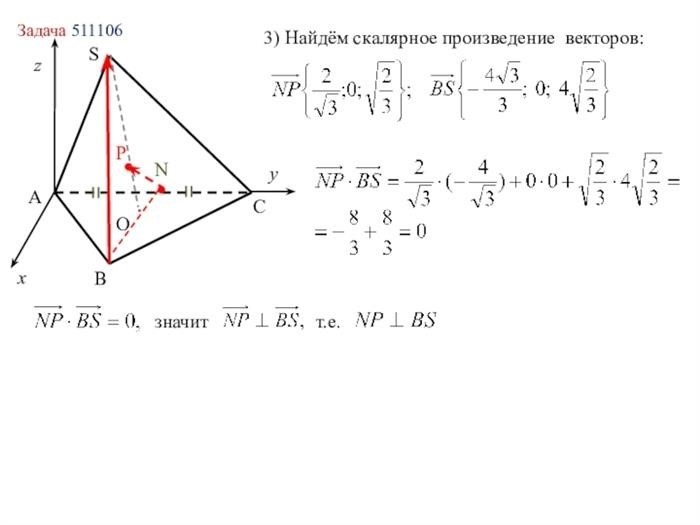
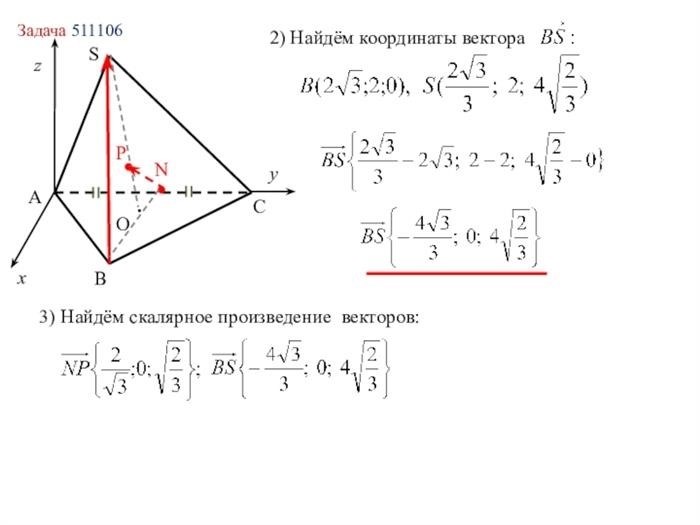
3. Векторный метод
Векторный метод основан на использовании векторных операций и позволяет более эффективно решать задачи, связанные с применением векторов. Данный метод позволяет учитывать не только положение точки относительно прямой, но и ее направление, что может быть важно в некоторых случаях. Для применения данного метода необходимо знать параметрическое уравнение прямой и координаты точки.
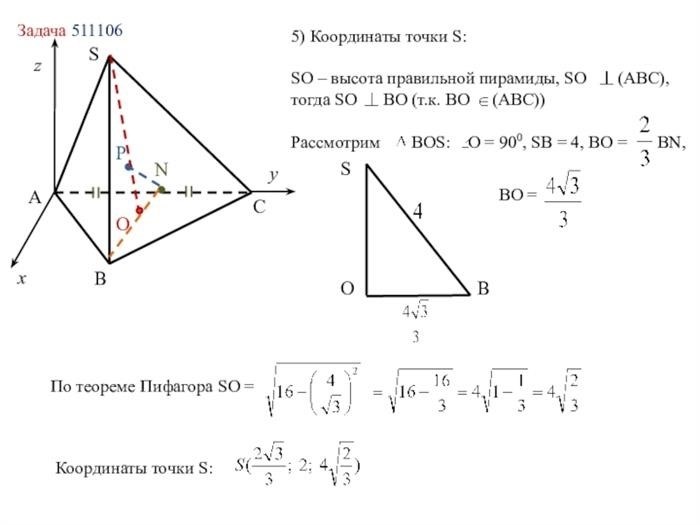
4. Координатный метод
Координатный метод основан на использовании координат точки и уравнений прямой в прямоугольной системе координат. Данный метод является наиболее распространенным и удобным, поскольку позволяет вычислить расстояние от точки до прямой с использованием известных координат. Для применения данного метода необходимо знать уравнение прямой и координаты точки.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Геометрический | – Наглядное представление задачи – Простота использования |
– Требуется геометрическая подготовка – Ограниченная применимость |
| Формульный | – Универсальность – Не требует построения геометрической модели |
– Требуется знание соответствующих формул и уравнений |
| Векторный | – Более эффективное решение задач с векторами | – Требуется знание параметрического уравнения прямой |
| Координатный | – Наиболее распространенный и удобный метод | – Требуется знание уравнения прямой и координат точки |
В итоге, выбор метода для вычисления расстояния от точки до прямой зависит от требуемой точности результата, доступных данных и уровня подготовки исполнителя задачи. В каждом конкретном случае целесообразно выбирать наиболее удобный и применимый метод для решения задачи.
Определение прямой и точки
Точка – это элементарное понятие геометрии, которое обозначает местоположение в пространстве или на плоскости. Точка не имеет размеров и представляет собой математическую абстракцию.
Координатный метод
В координатном методе прямая и точка определяются с помощью численных координат на плоскости. Координаты точки задаются уникальной парой чисел (x, y), где x – абсцисса точки, y – ордината точки.
Уравнение прямой
Прямую на плоскости можно задать уравнением вида ax + by + c = 0, где a, b и c – коэффициенты, определяющие положение прямой относительно осей координат.
Расстояние от точки до прямой
Расстояние от точки до прямой можно вычислить с помощью формулы, основанной на координатном методе. Для этого нужно знать координаты точки и коэффициенты прямой. Формула выглядит следующим образом:
d = |ax1 + by1 + c| / √(a2 + b2)
Пример
Дана прямая со следующими коэффициентами: a = 2, b = 3, c = 4. Найдем расстояние от точки P(1, 2) до этой прямой:
| Исходные данные | Расчеты | Ответ |
|---|---|---|
| a = 2, b = 3, c = 4 | d = |2*1 + 3*2 + 4| / √(2 2 + 3 2) | d = 8 / √13 ≈ 2.25 |
Таким образом, расстояние от точки P(1, 2) до прямой с коэффициентами a = 2, b = 3, c = 4 составляет около 2.25.
Что такое расстояние?
Расстояние имеет большое значение в различных областях науки и ежедневной жизни. Например, в физике расстояние может определять скорость движения объектов, уровень энергии или время, необходимое для перехода от одной точки к другой.
Как измеряется расстояние?
Расстояние может измеряться в разных единицах, в зависимости от контекста. Наиболее распространенными единицами измерения расстояния являются:
- Метр (м): основная международная единица измерения длины;
- Километр (км): равен 1000 метров;
- Миллиметр (мм): равен 0,001 метра;
- Сантиметр (см): равен 0,01 метра;
- Морская миля: равна приблизительно 1852 метрам;
- Фут: равен приблизительно 0,3048 метра;
- Дюйм: равен приблизительно 0,0254 метра.
Формула расстояния
Расстояние между двумя точками может быть вычислено с использованием различных формул, в зависимости от системы координат. В декартовой системе координат формула для вычисления расстояния между точками (x1, y1) и (x2, y2) представляет собой:
d = √((x2 – x1)² + (y2 – y1)²)
Эта формула основана на теореме Пифагора и позволяет нам найти прямое расстояние между двумя точками в плоском пространстве.
Применение в реальной жизни
Понимание расстояния имеет практическое применение в различных ситуациях, таких как:
- Навигация: расстояние помогает определить наиболее короткий путь от одного места к другому;
- Строительство: расстояние используется для планирования размещения зданий и инфраструктуры;
- Спорт: расстояние является важным фактором для тренировок и соревнований;
- Транспорт: расстояние определяет стоимость и время путешествия;
- Урожайность почвы: расстояние между растениями может влиять на качество и количество урожая.
Важно понимать, что расстояние может иметь как прямую, так и косвенную значимость в зависимости от контекста, в котором оно используется.
Расстояние – это важная величина, которая показывает, насколько далеко находятся две точки друг от друга. Оно измеряется в различных единицах и может быть вычислено с использованием соответствующих формул. Понимание расстояния имеет широкое применение в различных областях науки и повседневной жизни.
Как использовать формулу для расчета расстояния от точки до прямой?
Для определения расстояния от точки до прямой при помощи координатного метода можно использовать специальную формулу.
Формула для расчета расстояния от точки с координатами (x0, y0) до прямой в общем виде выглядит следующим образом:
d = |Ax0 + By0 + C| / √(A 2 + B 2)
Как использовать формулу для расчета расстояния?
- Запишите уравнение прямой в общем виде: Ax + By + C = 0, где A, B и C – коэффициенты.
- Определите значения коэффициентов A, B и C.
- Запишите координаты точки, от которой нужно найти расстояние, как (x0, y0).
- Подставьте значения A, B, C, x0 и y0 в формулу для расчета расстояния:
- Вычислите числитель формулы: Ax0 + By0 + C.
- Вычислите знаменатель формулы: √(A 2 + B 2).
- Найдите абсолютное значение числителя: |Ax0 + By0 + C|.
- Разделите найденное значение на значение знаменателя: |Ax0 + By0 + C| / √(A 2 + B 2).
- Полученное число будет являться искомым расстоянием от точки до прямой.
d = |Ax0 + By0 + C| / √(A 2 + B 2)
Пример использования формулы
Рассмотрим пример: у нас есть уравнение прямой 2x + 3y – 5 = 0 и точка с координатами (1, 2).
- Записываем уравнение прямой в общем виде: A = 2, B = 3, C = -5.
- Записываем координаты точки: x0 = 1, y0 = 2.
- Подставляем значения в формулу для расчета расстояния:
d = |2*1 + 3*2 – 5| / √(2 2 + 3 2)
- Вычисляем числитель формулы: 2*1 + 3*2 – 5 = 1.
- Вычисляем знаменатель формулы: √(2 2 + 3 2) = √(4 + 9) = √13.
- Находим абсолютное значение числителя: |1| = 1.
- Делим абсолютное значение числителя на знаменатель: 1 / √13.
Таким образом, расстояние от точки с координатами (1, 2) до прямой 2x + 3y – 5 = 0 равно 1 / √13.
Координаты точек: А(0/0/0)
Рассмотрим координаты точки А(0/0/0) в трехмерном пространстве. Точка А имеет нулевые координаты по осям x, y и z.
Координаты точки А в трехмерном пространстве:
- x = 0
- y = 0
- z = 0
Интерпретация координаты 0:
Координата 0 означает положение точки А на оси соответствующей координате. В данном случае, точка А находится в начале координатных осей и не имеет смещения ни по оси x, ни по оси y, ни по оси z.
Свойства точки А с координатами (0/0/0):
- Точка А является центром координатной системы.
- Относительно точки А другие точки могут быть расположены на расстоянии, задаваемом их координатами.
- Точка А является началом всех координатных осей.
- Точка А может служить основой для определения расстояния от других точек до прямой или плоскости.
Применение точки А в геометрии и физике:
Точка А с координатами (0/0/0) играет важную роль в геометрии и физике при определении положения и расстояний между объектами. Например, в геометрии точка А может быть связана с началом координат. В физике точка А может служить точкой отсчета для определения позиции тела в пространстве.
Что влияет на точность расчетов?
Точность расчетов в задачах, связанных с определением расстояния от точки до прямой координатным методом, зависит от нескольких факторов:
- Уравнение прямой;
- Координаты точки;
- Внимательность и точность выполнения расчетов.
Уравнение прямой
Уравнение прямой имеет важное значение для точности расчетов. Верное определение коэффициентов при иксе и игреке позволяет получить точные значения расстояния от точки до прямой. Ошибки в уравнении могут привести к неточным результатам.
Координаты точки
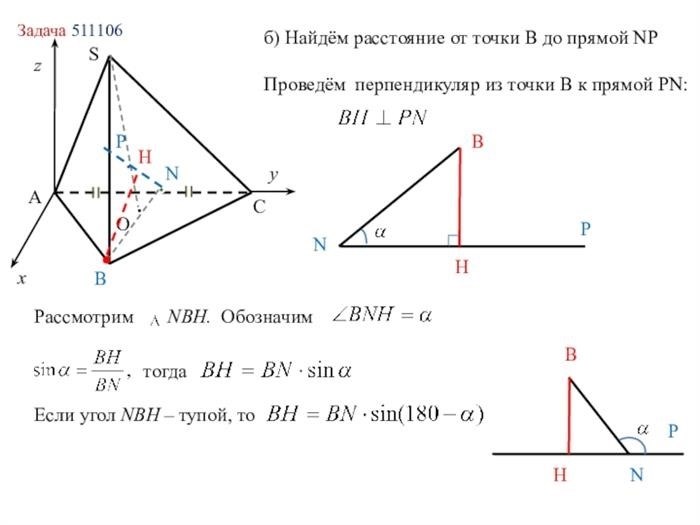
Точность расчетов также зависит от правильного определения координат точки. Допущение ошибок при определении координат может привести к неверному определению расстояния. Поэтому важно внимательно отслеживать и записывать координаты точки перед выполнением расчетов.
Внимательность и точность расчетов
Чтобы получить точные результаты, необходимо быть внимательным и точным при выполнении расчетов. Ошибки при операциях с числами могут привести к неточным значениям расстояния. Поэтому важно внимательно следить за каждым шагом расчета и проверять результаты на соответствие логике задачи.
Подписи к слайдам:
1. Наименование слайда:
Краткое и информативное наименование слайда позволяет сразу же определить его содержание и установить связь с темой презентации.
2. Текстовые подписи:
Текстовые подписи являются основным способом донесения информации на слайдах. Они могут содержать основные тезисы, вопросы, ключевые слова или фразы, примеры и иллюстрации. Текстовые подписи должны быть краткими, информативными и легко читаемыми.
3. Графические подписи:
Графические подписи используются для пояснения и дополнения графиков, диаграмм, иллюстраций и других визуальных элементов на слайдах. Они могут быть в виде стрелок, линий, шкал, подписей к осям или просто указывать на важные детали и особенности изображения.
4. Цитаты:
Цитаты могут быть использованы как подписи к слайдам, чтобы подкрепить иллюстрацию или привести авторитетные мнения и высказывания по теме презентации. Цитаты должны быть атрибутированы и отличаться от основного текста на слайде, например, быть выделенными курсивом или жирным шрифтом.
5. Таблицы и списки:
Таблицы и списки могут использоваться в качестве подписей к слайдам, чтобы систематизировать и структурировать информацию. Они помогают организовать данные, сравнить значения, выделить основные пункты и сделать презентацию более понятной и наглядной.
6. Ссылки и источники:
Подписи к слайдам также могут содержать ссылки на источники и дополнительные материалы, которые позволяют углубиться в тему презентации и проверить достоверность представленной информации.
Как измерить расстояние?
1. Измерение расстояния с помощью линейки:
Самый простой и доступный способ измерения расстояния – использование линейки. Линейку можно использовать для измерения расстояний в маломасштабных задачах, например, в строительстве или дизайне интерьера.
2. Измерение расстояния с помощью измерительной ленты:
Измерительная лента является более длинным и удобным инструментом для измерения расстояния. Она может использоваться для измерения длины объектов или расстояний с большей точностью, чем линейка.
3. Измерение расстояния с помощью лазерного измерителя:
Лазерный измеритель – это современный инструмент, который использует лазерный луч для измерения расстояний. Он может точно измерить расстояния на большие расстояния без необходимости прямого контакта с объектом.
4. Измерение расстояния с помощью геодезического инструмента:
Геодезический инструмент, такой как теодолит или тахеометр, используется для измерения расстояний и углов в геодезии и строительстве. Он обеспечивает высокую точность и может использоваться для сложных измерений на больших расстояниях.
5. Измерение расстояния с помощью других инструментов:
Кроме перечисленных выше инструментов, существуют и другие способы измерения расстояния, такие как применение ультразвуковых измерителей, GPS-навигация, использование спутниковой технологии и др.
Все эти методы позволяют измерить расстояние с разной степенью точности, в зависимости от требуемой задачи и доступных средств измерения. Выбор инструмента для измерения расстояния зависит от конкретной ситуации и требований к точности измерения.
Как найти уравнение прямой?
Существует несколько способов нахождения уравнения прямой – графический, аналитический и векторный. В данном тексте рассмотрим аналитический метод, который позволяет найти уравнение прямой по заданным условиям.
Шаги для нахождения уравнения прямой:
- Определение коэффициентов уравнения прямой
- Выбор известной точки на прямой
- Подстановка координат известной точки в уравнение прямой
- Решение уравнения для определения оставшегося неизвестного коэффициента
Определение коэффициентов уравнения прямой в данном методе осуществляется с помощью двух известных точек прямой или одной известной точки и значения углового коэффициента прямой.
Рассмотрим пример. Пусть даны две точки на прямой: A(x1, y1) и B(x2, y2). Задача состоит в нахождении уравнения прямой, проходящей через эти точки.
| Известные данные | Решение |
|---|---|
| x1 = 2, y1 = 3 | Координаты точки A |
| x2 = 4, y2 = 5 | Координаты точки B |
Выберем известную точку A и подставим ее координаты (x1, y1) в уравнение прямой y = kx + b:
y1 = k * x1 + b
Запишем это уравнение в более общем виде:
y = k * x + b
Теперь найдем значение второй известной точки B, подставив ее координаты (x2, y2) в уравнение прямой:
y2 = k * x2 + b
Решив уравнение для b, получим:
b = y2 - k * x2
Подставляем найденное значение b обратно в общее уравнение прямой:
y = k * x + (y2 - k * x2)
Упрощаем это уравнение:
y = kx + y2 - kx2
Итак, уравнение прямой, проходящей через точки A(x1, y1) и B(x2, y2), будет иметь вид:
y = kx + y2 - kx2
Таким образом, мы нашли уравнение прямой, используя метод аналитического нахождения коэффициентов. Этот метод позволяет найти уравнение прямой по двум известным точкам прямой.
Как найти координаты точки?
Координаты точки могут быть найдены различными способами в зависимости от ситуации и доступной информации. В предыдущих разделах мы рассмотрели несколько методов определения координат точки по заранее известным данным, таким как расстояние от точки до начала координат или расстояния от точки до прямой.
Однако существуют и другие методы определения координат точки, такие как использование геодезических данных, GPS-навигации или анализа изображений. В зависимости от задачи и доступной информации, нужно выбирать наиболее подходящий метод.
Если у вас есть координаты других точек и известно, какая из них соответствует искомой точке, можно использовать методы интерполяции или экстраполяции для определения координат. Также можно использовать методы триангуляции или мультилатерации для определения координат точки относительно нескольких других точек.
Итак, чтобы найти координаты точки, необходимо использовать доступные данные и методы, которые лучше всего подходят для вашей конкретной задачи. Важно помнить, что точность определения координат зависит от точности доступной информации и используемого метода. Иногда может потребоваться комбинирование нескольких методов или использование дополнительных данных для повышения точности и достоверности результата.