Перемещение – величина в физике, характеризующая изменение местоположения тела за определенное время. При прямолинейном равномерном движении перемещение определяется как произведение скорости на время. Эта величина имеет направление и может быть положительной или отрицательной, в зависимости от направления движения. Значение перемещения можно измерить в метрах (м) или других единицах длины. Перемещение имеет важное значение в динамике и кинематике, позволяя определить путь, пройденный объектом, и расстояние между двумя точками. Также перемещение используется для расчета средней скорости и других величин движения.
Равномерное и неравномерное движение
Равномерное движение
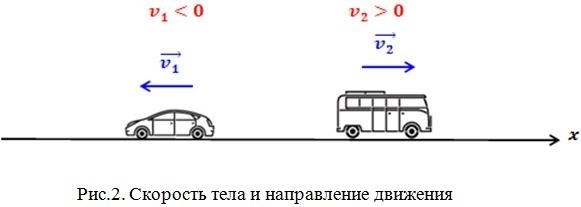
Равномерное движение – это движение тела, при котором за равные промежутки времени оно перемещается на одинаковые расстояния. В равномерном движении скорость тела остается постоянной.
Характеристики равномерного движения:
- Постоянная скорость
- Прямолинейное направление
- Равные промежутки пройденного пути за равные промежутки времени
Неравномерное движение
Неравномерное движение – это движение тела, при котором оно занимает каждый следующий участок пути за разные промежутки времени. В неравномерном движении скорость тела изменяется.
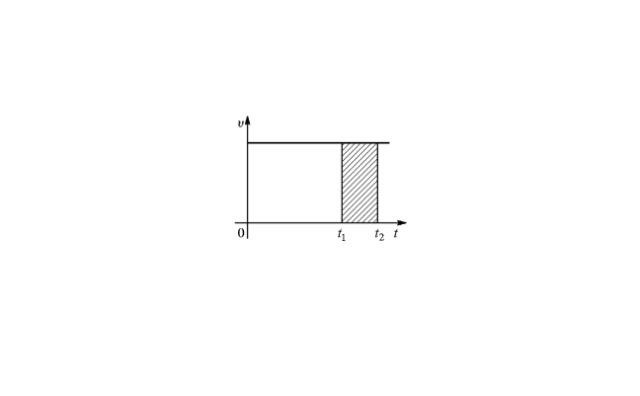
Характеристики неравномерного движения:
- Меняющаяся скорость
- Произвольное направление
- Разные промежутки пройденного пути за равные промежутки времени
Примеры неравномерного движения:
- Автомобиль, разгоняющийся с места
- Камень, падающий с высоты под действием гравитации
- Лодка, движущаяся в реке против течения
Сравнение равномерного и неравномерного движения
| Характеристика | Равномерное движение | Неравномерное движение |
|---|---|---|
| Скорость | Постоянная | Меняющаяся |
| Направление | Прямолинейное | Произвольное |
| Пройденный путь | Равные промежутки времени | Разные промежутки времени |
Прямолинейное движение вдоль оси
Скорость
Скорость тела при прямолинейном движении вдоль оси – это величина, которая показывает, на сколько единиц (например, метров) перемещается тело за единицу времени (например, секунду).
Формула скорости
Скорость можно вычислить по формуле: v = S / t, где v – скорость, S – пройденное расстояние, t – время, за которое пройдено расстояние.
Ускорение
Ускорение тела при прямолинейном движении вдоль оси – это величина, которая показывает, на сколько единиц в секунду изменяется скорость тела.
Формула ускорения
Ускорение можно вычислить по формуле: a = (v2 – v1) / t, где a – ускорение, v1 и v2 – начальная и конечная скорости, t – время, за которое изменяется скорость.
График прямолинейного движения
На графике прямолинейного движения вдоль оси время откладывается по горизонтальной оси, а пройденное расстояние – по вертикальной оси. Таким образом, можно наглядно представить, как меняется положение тела во времени.
| Время, t | Пройденное расстояние, S |
|---|---|
| 0 | 0 |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
Закон инерции
Когда тело движется прямолинейно вдоль оси, оно сохраняет свою скорость и направление движения, если на него не действуют внешние силы.
“Прямолинейное движение вдоль оси – это одно из самых простых и понятных видов движения, которое легко описывается с помощью основных формул и понятий. Оно встречается как в механике, так и в жизни.”
Параметры, описывающие движение
При изучении прямолинейного равномерного движения необходимо учитывать ряд параметров, которые позволяют полноценно описать данную физическую величину. Рассмотрим основные параметры:
Скорость
Скорость является важнейшим параметром движения. Она определяется как отношение пройденного расстояния к промежутку времени. Символически скорость обозначается буквой v. В прямолинейном равномерном движении скорость не изменяется, поэтому можно говорить о постоянной скорости.
Расстояние
Расстояние представляет собой смещение объекта по прямой. В отличие от пройденного пути, расстояние является скалярной величиной и указывает на общую длину перемещения. Обозначается буквой s.
Пройденный путь
Пройденный путь – это путь, пройденный объектом во время движения от начального положения до конечного. Он также измеряется в длине, но в отличие от расстояния является векторной величиной, так как указывает на направление перемещения.
Время
Время – это длительность движения. Оно может быть измерено в секундах, минутах, часах и т.д. В прямолинейном равномерном движении время также является постоянным, так как скорость не меняется.
Ускорение
Ускорение – это изменение скорости во времени. В прямолинейном равномерном движении ускорение равно нулю, так как скорость объекта остается постоянной. Ускорение обозначается буквой a.
Итак, при изучении прямолинейного равномерного движения важно учитывать параметры, такие как скорость, расстояние, пройденный путь, время и ускорение. Эти параметры позволяют полноценно описать движение объекта в пространстве и времени.
Как определить скорость по графику перемещения?
Важно отметить, что скорость в прямолинейном равномерном движении остается постоянной во времени. Это значит, что график перемещения будет представлять собой прямую линию, соответствующую равномерному изменению положения объекта.

Методы определения скорости по графику перемещения:
- Измерение наклона графика: если график является прямой линией, то его наклон будет соответствовать скорости объекта (скорость равна тангенсу угла наклона графика).
- Расчет скорости методом среднего значения: можно разделить разность перемещения объекта на разность времени, чтобы получить среднюю скорость объекта на данном участке графика перемещения.
- Определение скорости по изменению времени: если известно изменение времени, то можно определить соответствующее изменение положения объекта и вычислить скорость.
Пример определения скорости по графику перемещения:
Пусть у нас есть график перемещения объекта, который представляет собой прямую линию. Измерим наклон этой линии и получим значение 10 м/с. Значит, скорость объекта равна 10 м/с. Это означает, что объект перемещается на 10 метров каждую секунду.
Таким образом, анализируя график перемещения объекта, мы можем определить его скорость. Этот метод является одним из способов измерения скорости в физике и позволяет получить количественное значение скорости объекта в прямолинейном равномерном движении.
Формулы скорости и перемещения в векторной форме
Для описания прямолинейного равномерного движения существуют формулы скорости и перемещения, которые могут быть выражены в векторной форме. Эти формулы позволяют определить направление и модуль скорости и перемещения объекта.
Формула скорости в векторной форме
Скорость в векторной форме представляет собой векторную величину и определяется как величина перемещения объекта на единицу времени. Формула скорости в векторной форме выглядит следующим образом:
Вектор скорости (v) = Δs / Δt
где Δs – вектор перемещения объекта, а Δt – интервал времени, за который происходит перемещение.
Формула перемещения в векторной форме
Перемещение также является векторной величиной и представляет собой разность между конечной и начальной точками объекта. Формула перемещения в векторной форме выглядит следующим образом:
Вектор перемещения (Δs) = конечная точка – начальная точка
где конечная точка – точка, в которой находится объект после перемещения, а начальная точка – точка, в которой находился объект до перемещения.
Примеры использования формул скорости и перемещения в векторной форме
Рассмотрим пример использования формул скорости и перемещения в векторной форме. Предположим, что объект переместился на 10 м вперед и на 5 м вправо за 2 секунды. Сначала определим вектор перемещения:
Вектор перемещения (Δs) = (10 м вперед) + (5 м вправо) = (10 м, 5 м)
Затем определим вектор скорости по формуле:
Вектор скорости (v) = Δs / Δt = (10 м, 5 м) / 2 с = (5 м/с вперед, 2.5 м/с вправо)
Таким образом, наш объект имеет скорость 5 м/с вперед и 2.5 м/с вправо.
Формулы скорости и перемещения в векторной форме позволяют определить направление и модуль скорости и перемещения объекта при прямолинейном равномерном движении. Используя эти формулы, можно более точно описывать движение объектов и предсказывать их перемещение на основе имеющихся данных.
График уравнения равномерного движения
Для построения графика уравнения равномерного движения необходимо знать две основные характеристики: начальное положение тела и его скорость. Эти параметры влияют на форму графика и его параметры, такие как наклон и смещение.
Основные элементы графика уравнения равномерного движения:
- Начальное положение: это значение координаты тела в начальный момент времени. Оно определяет вертикальное смещение графика.
- Скорость: это величина, определяющая наклон графика. Чем больше скорость тела, тем круче будет наклон графика.
- Время: ось графика, на которой откладывается время. На этой оси отображается время, прошедшее с начала движения тела.
- Положение тела: ось графика, на которой откладывается положение тела. Значение положения для каждого момента времени отображается в виде точек на графике.
Пример графика уравнения равномерного движения:
| Время (сек) | Положение (м) |
|---|---|
| 0 | 0 |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
На приведенной таблице представлен пример графика уравнения равномерного движения. В начальный момент времени (0 сек) тело находится в начальном положении (0 м), затем с каждой секундой его положение увеличивается на 10 м. Таким образом, на графике видно прямолинейное увеличение положения с течением времени.
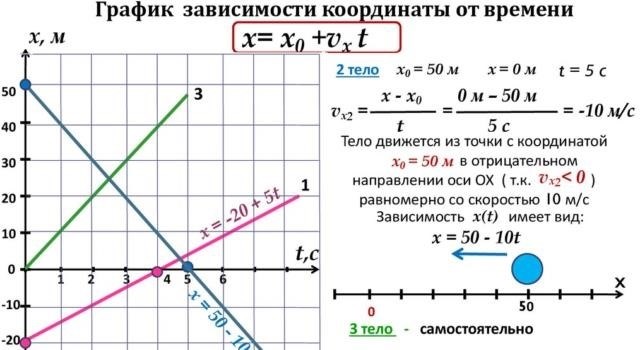
График уравнения равномерного движения является удобным инструментом для анализа и прогнозирования движения тел. Он позволяет определить, как будет изменяться положение тела в будущем и предсказать его положение в любой момент времени.
Модуль вектора перемещения и путь
Величина пути – это мера пройденного пространства при движении объекта. Она также является положительным числом и определяется как длина кривой, по которой прошел объект.
Модуль вектора перемещения
- Определение: Модуль вектора перемещения – это длина вектора, который указывает направление и длину перемещения объекта.
- Единицы измерения: Модуль вектора перемещения измеряется в метрах (м) или в других единицах длины, в зависимости от системы измерений.
- Вычисление: Модуль вектора перемещения вычисляется по формуле |r| = √(x² + y² + z²), где x, y, z – координаты точки, в которой находится объект.
Путь
- Определение: Путь – это мера пройденного пространства при движении объекта из одной точки в другую.
- Единицы измерения: Путь измеряется в метрах (м) или в других единицах длины, в зависимости от системы измерений.
- Вычисление: Путь вычисляется как сумма длин всех участков пути от начальной до конечной точки.
- Отличие от модуля вектора перемещения: В отличие от модуля вектора перемещения, путь может быть больше или равен модулю вектора перемещения, так как путь учитывает пройденное пространство по всей кривой, а модуль вектора перемещения учитывает только расстояние между начальной и конечной точками.
Движение на плоскости или в пространстве
Движение на плоскости
Движение на плоскости характеризуется перемещением объекта только в двух измерениях – вперед-назад (по горизонтали) и влево-вправо (по вертикали). Для описания и анализа такого движения используются оси координат X и Y.
Основные характеристики движения на плоскости:
- Скорость: скорость объекта на плоскости определяется как отношение пройденного расстояния к затраченному времени. Он может быть постоянным или меняться в течение движения.
- Ускорение: ускорение объекта на плоскости – это изменение его скорости по времени. Ускорение может быть постоянным или переменным.
- Траектория: траектория движения – это путь, который пройдет объект на плоскости в результате его перемещения. Траектория может быть прямой, криволинейной или замкнутой.
Движение в пространстве
Движение в пространстве представляет собой перемещение объекта не только по горизонтали и вертикали, но и по третьему измерению – вверх и вниз (ось Z). Для описания и анализа такого движения используются оси координат X, Y и Z.
Основные особенности движения в пространстве:
- Скорость: скорость объекта в пространстве определяется как отношение пройденного расстояния к затраченному времени. Она может быть постоянной или меняться в течение движения.
- Ускорение: ускорение объекта в пространстве – это изменение его скорости по времени. Ускорение может быть постоянным или переменным.
- Траектория: траектория движения – это путь, который пройдет объект в результате его перемещения в пространстве. Траектория может быть прямой, криволинейной или замкнутой.
Кроме того, при движении в пространстве возможны различные типы координатных систем, такие как прямоугольная, сферическая и цилиндрическая, которые используются для более точного определения положения объекта в пространстве.
Скорость равномерного движения
Понятие равномерного движения
Равномерное движение – это движение, при котором тело перемещается по прямой линии с постоянной скоростью. В данном случае скорость не изменяется со временем, поэтому перемещение тела пропорционально продолжительности движения.
Вычисление скорости равномерного движения
Формула для вычисления скорости равномерного движения выглядит следующим образом:
Скорость (V) = Расстояние (S) / Время (t)
Используя эту формулу, можно вычислить скорость, зная пройденное расстояние и время, за которое это расстояние было преодолено.
Примеры скорости равномерного движения
Вот несколько примеров скорости равномерного движения:
- Автомобиль движется по прямой дороге со скоростью 60 км/ч. За 1 час он пройдет 60 километров.
- Велосипедист едет со скоростью 5 м/с. За 10 секунд он преодолеет расстояние в 50 метров.
Таблица скорости равномерного движения
| Расстояние (S) | Время (t) | Скорость (V) |
|---|---|---|
| 100 метров | 10 секунд | 10 м/с |
| 500 метров | 1 минута | 8.33 м/с |
Скорость равномерного движения является важной физической величиной, которая показывает, как быстро тело перемещается по прямой линии. Вычисление скорости происходит путем деления пройденного расстояния на время движения. Отсутствие изменений скорости во время равномерного движения позволяет проще осуществлять его изучение и прогнозировать перемещение тела в будущем.
§ 4. Перемещение при прямолинейном равномерном движении
Определение и обозначение перемещения
Перемещение обозначается символом S. Оно является векторной величиной, то есть имеет направление и модуль, равный расстоянию между начальной и конечной точками.
Перемещение обычно измеряется в метрах (м) или в километрах (км), в зависимости от масштаба движения.
Признаки прямолинейного равномерного движения
Прямолинейное равномерное движение характеризуется следующими признаками:
- Траектория движения является прямой линией.
- Скорость тела постоянна во все моменты времени.
- Ускорение тела равно нулю.
Формула для расчета перемещения
Перемещение можно рассчитать с использованием формулы:
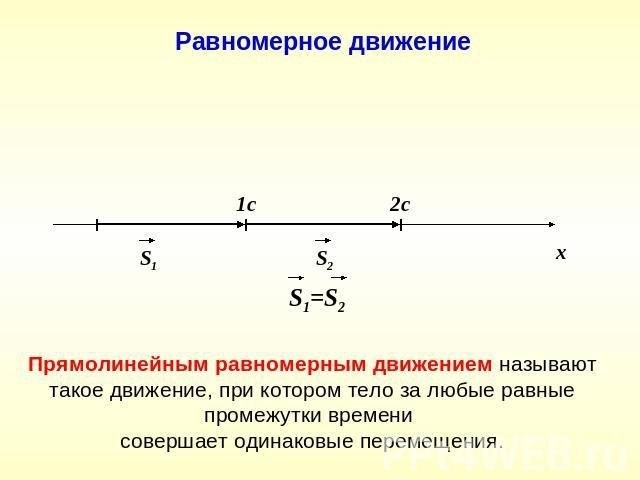
S = v * t
где v – скорость тела, t – время движения.
Пример применения формулы
Например, если тело движется со скоростью 10 м/с в течение 5 секунд, то его перемещение будет равно:
S = 10 м/с * 5 с = 50 м
Таблица перемещений при разных скоростях и временах движения
| Скорость (м/с) | Время (сек) | Перемещение (м) |
|---|---|---|
| 5 | 3 | 15 |
| 15 | 2 | 30 |
| 20 | 4 | 80 |
Перемещение при прямолинейном равномерном движении является важной характеристикой, которая позволяет определить расстояние между начальной и конечной точками движения. Оно рассчитывается с использованием формулы S = v * t. При прямолинейном равномерном движении траектория является прямой линией, скорость постоянна, а ускорение равно нулю.
Что мы узнали?
В результате изучения темы “Перемещение при прямолинейном равномерном движении” мы получили следующие знания:
1. Равномерное движение
Мы узнали, что равномерное движение характеризуется постоянной скоростью и отсутствием ускорения. Время, пройденное телом, пропорционально пройденному пути: s = v * t.
2. Формулы перемещения
Мы разобрали базовые формулы для расчета перемещения при равномерном движении:
- Скорость: v = s / t
- Время: t = s / v
3. Связь скорости и времени
Мы установили связь между скоростью тела и временем, затраченным на его перемещение. Чем больше скорость, тем меньше нужно времени для преодоления определенного расстояния.
4. Примеры задач
Мы рассмотрели несколько примеров задач, в которых нужно было рассчитать перемещение при равномерном движении. Это помогло нам лучше понять, как применять полученные формулы на практике и решать подобные задачи.
5. Векторное и скалярное представление
Мы изучили различные способы представления перемещения: векторное и скалярное. Векторное представление учитывает не только величину перемещения, но и его направление, а скалярное представление упрощает расчеты, игнорируя направление.
6. Различные единицы измерения
Мы узнали, что перемещение измеряется в метрах (м), а скорость – в метрах в секунду (м/с). При необходимости, перемещение и скорость могут быть переведены в другие единицы измерения, такие как километры (км) или километры в час (км/ч).
7. Применение в реальной жизни
Мы обсудили применение знаний о перемещении при равномерном движении в реальной жизни. Такие знания могут быть полезны в различных сферах, например, в автомобильной промышленности для расчета времени и расстояния путешествия между городами, или в физике для изучения траекторий движения тел.
Формула перемещения для практического использования
Практическое использование формулы перемещения позволяет получить точные данные о пройденном расстоянии объекта во времени, что может быть важным в таких случаях, как планирование маршрутов, определение времени прибытия или оценка скорости движения объекта.
Формула перемещения и её значение
Формула перемещения является одной из основных формул механики и представляет собой следующее выражение:
s = v * t
- s – перемещение объекта, выраженное в длине;
- v – скорость объекта, выраженная в длине за единицу времени;
- t – время, в течение которого происходит движение объекта.
Данная формула позволяет рассчитать пройденное расстояние объекта, зная его скорость и время движения. Значение формулы перемещения может быть полезно во многих ситуациях, когда необходимо определить точное расстояние, пройденное объектом.
Пример использования формулы перемещения
Для более наглядного примера использования формулы перемещения рассмотрим следующую ситуацию.
Предположим, что автомобиль движется со скоростью 60 км/ч в течение 2 часов. Для определения расстояния, пройденного автомобилем, необходимо применить формулу перемещения:
s = v * t
s = 60 км/ч * 2 ч = 120 км
Таким образом, автомобиль пройдет расстояние в 120 километров за указанное время.
Формула перемещения является важным инструментом для расчета пройденного расстояния объектом при прямолинейном равномерном движении. Ее практическое использование позволяет получить точные данные о перемещении объекта во времени, что может быть полезно в различных сферах жизни и научных исследованиях.
Формула перемещения для одномерного случая
Рассмотрев прямолинейное равномерное движение, можно понять, что для описания перемещения тела необходимо использовать определенную формулу. Эта формула связывает перемещение, скорость и время движения тела.
Одним из основных понятий в рамках данной темы является формула перемещения, которая выражается следующим образом:
С = V * t
Где:
- С – перемещение тела за время t;
- V – скорость движения тела;
- t – время, в течение которого происходит движение.
Формула перемещения позволяет определить расстояние, которое перемещается тело за определенное время. Она является одной из ключевых формул в физике и находит широкое применение при решении задач, связанных с движением тел.
Используя данную формулу, можно рассчитать перемещение тела в одномерном случае, когда движение происходит только вдоль одной оси. Например, если известна скорость тела и время движения, то можно определить, какое расстояние оно пройдет.
В конечном итоге, формула перемещения является важным инструментом для анализа и описания прямолинейного равномерного движения. Эта формула позволяет определить, сколько расстояния пройдет тело за определенное время, и является основой для решения задач связанных с перемещением тел на практике.