Признак параллельности прямой и плоскости: прямая и плоскость параллельны, если прямая не пересекает плоскость и если прямая параллельна любой прямой, проходящей в данной плоскости.
Теорема о параллельности прямой и плоскости
Теорема: Если прямая перпендикулярна плоскости, то она параллельна любой другой плоскости, содержащей первую плоскость.
Доказательство:
- Пусть дана прямая m, перпендикулярная плоскости АВСD.
- Пусть также дана плоскость МНКL, которая содержит плоскость АВСD.
- Допустим, прямая m не параллельна плоскости МНКL.
- Тогда существует точка Е на прямой m, такая что прямая ЕР пересекает плоскость МНКL в точке Р.
- Так как прямая m перпендикулярна плоскости АВСD, то она также перпендикулярна плоскости МНКL.
- Таким образом, прямая ЕР должна быть перпендикулярна и прямой PQ, где точка Q лежит на прямой ЕР.
- Продлим прямую m до пересечения с прямой PQ. Пусть это будет точка F.
- Так как прямая ЕР перпендикулярна прямой PQ, то угол между прямой EF и прямой ЕР также будет прямым.
- Но вспомним, что прямая EF лежит в плоскости МНКL, а прямая ЕР пересекает эту плоскость, значит угол между прямыми EF и ЕР не может быть прямым.
- Полученное противоречие указывает на то, что допущение о том, что прямая m не параллельна плоскости МНКL, неверно.
- Следовательно, прямая m параллельна любой другой плоскости, содержащей плоскость АВСD.
Следствие:
Если две плоскости перпендикулярны друг к другу, то любая прямая, перпендикулярная одной из плоскостей, будет также параллельна другой плоскости.
Признаки и условия параллельности
Параллельными называют прямую и плоскость, если все прямые, лежащие в этой плоскости и перпендикулярные данной прямой, также параллельны между собой.
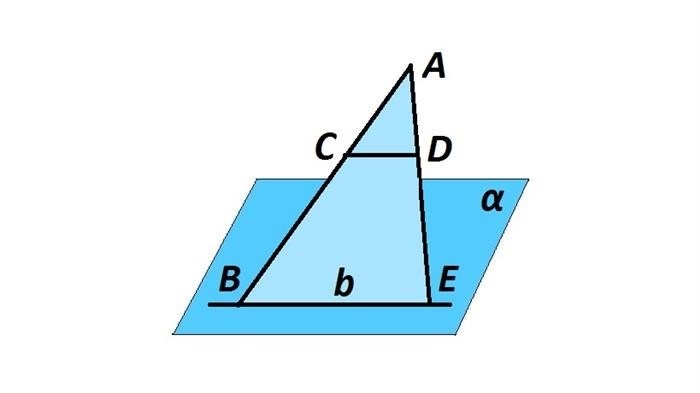
Существуют несколько признаков и условий, которые помогают определить, являются ли прямая и плоскость параллельными:
Условие перпендикулярности к нормали плоскости
Прямая и плоскость параллельны, если вектор направления прямой перпендикулярен нормали плоскости. Или же, если угол между вектором направления прямой и нормалью к плоскости равен 90 градусам.
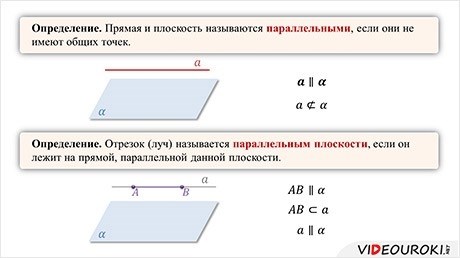
Условие перпендикулярности к двум прямым на плоскости
Прямая и плоскость параллельны, если данная прямая перпендикулярна двум любым пересекающимся на плоскости прямым.
Условие равенства углов
Прямая и плоскость параллельны, если углы между прямой и плоскостью равны между собой. Или же, если соответствующие углы, образованные прямой и плоскостью при пересечении, равны.
Условие равенства отношений длин
Прямая и плоскость параллельны, если отношение длин отрезков, проведенных из точки на прямой до пересечения прямой с плоскостью, равно.
- Если выполняется хотя бы одно из вышеуказанных условий, то прямая и плоскость являются параллельными.
- Если отрицается каждое из условий, то прямая и плоскость не являются параллельными, а пересекаются.
Подписи к слайдам:
На слайдах представлены различные примеры параллельных прямых и плоскостей. Обратите внимание на следующие особенности:
- Слайд 1: Демонстрация концепции параллельности прямых на двумерной плоскости.
- Слайд 2: Иллюстрация параллельности двух плоскостей в трехмерном пространстве.
- Слайд 3: Визуализация параллельности прямой и плоскости, где прямая лежит в плоскости.
- Слайд 4: Пример параллельности прямой и плоскости, где прямая пересекает плоскость.
Итак, параллельность прямой и плоскости характеризуется тем, что прямая не пересекает данную плоскость и лежит в параллельной ей плоскости.