Числа и цифры играют важную роль в нашей жизни, однако многие люди не знают, чем они отличаются друг от друга. Число – это абстрактное понятие, которое обозначает количество или порядок предметов или явлений. С другой стороны, цифра – это символ или знак, который представляет числовую информацию. Используя цифры, мы можем записать и представить числа. Различие между числом и цифрой важно понимать, чтобы правильно использовать их в различных контекстах и ситуациях.
Классическая запись чисел римскими цифрами
Основные римские цифры
В римской системе существуют основные цифры, которым соответствуют определенные символы:
- I – 1
- V – 5
- X – 10
- L – 50
- C – 100
- D – 500
- M – 1000
Используя эти символы, можно составлять и записывать числа. При этом существуют определенные правила сочетания символов.
Правила записи чисел
Правила записи чисел римскими цифрами следующие:
- Символы записываются слева направо, от больших к меньшим. Исключение составляют случаи, когда символ меньшего значения идет перед символом большего значения и образует так называемое вычитание.
- Вычитание происходит только в случаях сочетания символов I, X и C с символами более высокого значения. Например, IV обозначает 4 (5-1), а IX – 9 (10-1).
- Сумма символов, записанных слева направо, определяет итоговое значение числа. Например, VI обозначает 6 (5+1).
- Не существует нуля в системе римских чисел, поэтому отсутствие записи символов подразумевает значение 0.
Примеры записи чисел
Приведем несколько примеров записи чисел римскими цифрами:
- XIV – 14 (10+4)
- LIX – 59 (50-1+10)
- XCIII – 93 (100-10+1+1+1)
- CDXLIV – 444 (500-100+50-1+5)
Использование римской системы чисел в настоящее время
В настоящее время классическая запись чисел римскими цифрами используется редко и в основном в исторических или стилизованных контекстах. Однако некоторые символы, такие как I, V и X, все еще используются для обозначения порядковых чисел (например, I – 1-й, V – 5-й).
Знание записи чисел римскими цифрами является интересным историческим фактом, который помогает понять развитие математических систем и культурных особенностей древних цивилизаций.
Чтение и произношение целых чисел и десятичных дробей
Чтение целых чисел
Чтение целых чисел следует определенным правилам. В основе этих правил лежит умение разбивать число на разряды и читать каждый разряд отдельно. Вот некоторые примеры:
- Целое число 123456 читается как “сто двадцать три тысячи четыреста пятьдесят шесть”.
- Целое число 987654321 читается как “девятьсот восемьдесят семь миллионов шестьсот пятьдесят четыре тысячи триста двадцать один”.
Следует отметить, что числа с нулями в середине могут читаться по-разному в зависимости от контекста. Например, число 102 читается как “сто два” или “сто двадцать два”.
Чтение десятичных дробей
Десятичные дроби также имеют свои правила чтения. Они основаны на разделении дробной части на цифры и их последовательном чтении. Вот примеры:
- Десятичная дробь 0.25 читается как “ноль целых двадцать пять сотых”.
- Десятичная дробь 3.14159 читается как “три целых сто сорок одна тысячная пятьсот девяносто девять миллионных”.
Важно помнить, что десятичные дроби можно прочитать как обычные числа, например, число 0.5 можно прочитать как “половина”, а число 1.75 как “одна целая семьдесят пять сотых”.
Произношение чисел в таблице
| Число | Чтение |
|---|---|
| 0.01 | ноль целых одна сотая |
| 0.1 | ноль целых одна десятая |
| 0.5 | ноль целых пять десятых |
| 1.25 | одна целая двадцать пять сотых |
Это лишь некоторые примеры правил чтения и произношения целых чисел и десятичных дробей. В основе этих правил лежит умение разбивать числа на разряды и читать каждый разряд отдельно. Это поможет вам лучше понять и использовать числа в своей повседневной жизни и при работе с математикой.
Какие виды чисел изучаются в начальной школе?
Натуральные числа
- Натуральные числа – это числа, которые используются для обозначения количества предметов, людей, времени и других объектов. Они начинаются с единицы и не имеют нижней границы.
- Примеры натуральных чисел: 1, 2, 3, 4, 5…
Целые числа
- Целые числа включают натуральные числа и их отрицательные значения, а также число 0.
- Примеры целых чисел: -3, -2, -1, 0, 1, 2, 3…
Рациональные числа
- Рациональные числа – это числа, которые можно представить в виде обыкновенной или десятичной дроби.
- Примеры рациональных чисел: 1/2, 0.25, 5/3, -2/7…
Иррациональные числа
- Иррациональные числа – это числа, которые нельзя представить в виде обыкновенной или десятичной дроби.
- Примеры иррациональных чисел: √2, π, e, √3…
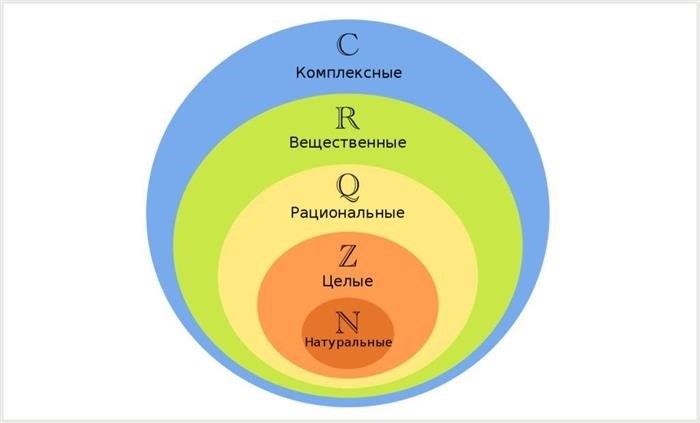
Вещественные числа
- Вещественные числа – это числа, которые включают в себя как рациональные, так и иррациональные числа.
- Примеры вещественных чисел: 2, -1.5, 0, √5, π…
Изучение этих видов чисел в начальной школе является важным этапом в формировании базовых математических навыков у детей. Они изучают свойства, операции и взаимосвязи между разными видами чисел, что позволяет им развивать логическое мышление и способности к анализу.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0 – ноль
Ноль – это символ, которым обозначают отсутствие или отсутствие количества. В математике ноль является вырожденным числом, которое не имеет значения во многих выражениях. Он также является основой для формирования чисел через счет.
1 – один
Единица – это самое простое и наименьшее число. Она используется как базовое число в многих математических операциях и функциях. Одна также может обозначать единство, первое место или начало чего-либо.

2 – два
Два – это число, которое следует за единицей. Оно обозначает двойственность или наличие двух элементов. Два также может использоваться для обозначения пары или сравнения двух вещей.
3 – три
Три – это число, следующее за двуми. Оно обозначает тройственность или наличие трех элементов. Три используется во многих культурах и религиях как символ полной гармонии и совершенства.
4 – четыре
Четыре – это число, которое следует за тремя. Оно обозначает наличие четырех элементов или деление на четыре части. Четыре также может использоваться для обозначения сезонов, например, в четырехквартирном году.
5 – пять
Пять – это число, которое следует за четырьмя. Оно обозначает наличие пяти элементов или деление на пять частей. Пять используется во многих областях, например, для обозначения пятой точки, меры или классификации.
6 – шесть
Шесть – это число, которое следует за пятью. Оно обозначает наличие шести элементов или шеститочечной системы. Шесть также может быть связано с временем и делиться на шесть частей суток или делить год на шесть временных периодов.
7 – семь
Семь – это число, которое следует за шестью. Оно обозначает наличие семи элементов или деление на семь частей. Семь также является числом счастливого случая во многих культурах и аспектов жизни.
8 – восемь
Восемь – это число, которое следует за семью. Оно обозначает наличие восьми элементов или деление на восемь частей. Восемь также может быть связано со сдвигом, циклами и повторами.
9 – девять
Девять – это число, которое следует за восьмью. Оно обозначает наличие девяти элементов или деление на девять частей. Девять также может быть связано с завершением, последним шагом или конечной точкой чего-либо.
Чем отличается цифра от числа?
Цифра
Цифра – это знак или символ, используемый для обозначения количества или порядка. Цифры образуют числовые системы и используются для записи числовых значений.
Основные характеристики цифр:
- Ограниченный набор символов: в десятичной системе мы используем цифры от 0 до 9.
- Множественное использование: цифры могут быть комбинированы для формирования числовых значений различной длины.
- Порядок: цифры могут иметь свое место в числовом ряду, определяя порядок и значение числа.
Примеры цифр:
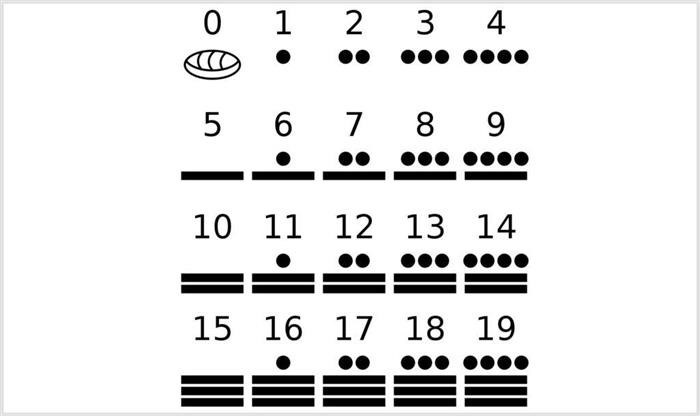
- 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
Цифры используются в различных областях науки, техники, экономики и повседневной жизни для представления конкретных числовых значений и операций.
Число
Число – это абстрактное понятие, обозначающее количество или единицу измерения. Число не зависит от системы счисления и может быть представлено различными цифрами.
Основные характеристики чисел:
- Абстрактность: число является абстрактным понятием и может быть выражено различными способами.
- Измерение и количество: число может представлять собой измерение или количество предметов или явлений.
- Математические операции: числа могут быть использованы для выполнения математических операций, таких как сложение, вычитание, умножение и деление.
Примеры чисел:
- 5
- 10
- 3.14
- 1000
- -7
Числа используются в математике, физике, экономике и других науках для измерения и анализа конкретных значений и свойств явлений и объектов.
Таким образом, цифра и число – два различных понятия, которые имеют свои уникальные характеристики и применение. Цифра является символом, используемым для обозначения количества или порядка в числовых системах, в то время как число представляет собой абстрактное понятие, обозначающее количество или измерение. Цифры могут быть использованы для формирования чисел различной длины и выполнения математических операций.
Какими бывают числа (школьная программа)
В школьной математике мы знакомимся с различными типами чисел. Каждый из них имеет свои особенности и применения.
Натуральные числа
Натуральные числа – это числа, которые используются для подсчета предметов или людей в количестве. Они начинаются с единицы и не имеют десятичных дробей или знака минус. Примеры: 1, 2, 3, 4 и так далее.
Целые числа
Целые числа – это набор натуральных чисел, включающих в себя также отрицательные числа и ноль. Они используются для представления долгов, температур, высоты под землей и других величин. Примеры: -3, -2, -1, 0, 1, 2, 3 и так далее.
Рациональные числа
Рациональные числа – это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Они включают в себя обыкновенные дроби и десятичные дроби. Примеры: 1/2, 0.5, -3/4, 2.25 и так далее.
Иррациональные числа
Иррациональные числа – это числа, которые нельзя представить в виде дроби и имеют бесконечное количество десятичных знаков без повторения. Примеры: √2, π (пи), e (экспонента) и так далее.
Трансцендентные числа
Трансцендентные числа – это подмножество иррациональных чисел, которые не являются корнями никакого алгебраического уравнения с целыми коэффициентами. Примеры: e (экспонента) и π (пи).
Пример сравнения разных типов чисел:
- Натуральное число: 3
- Целое число: -5
- Рациональное число: 1/2
- Иррациональное число: √2
- Трансцендентное число: e (экспонента)
Таблица различных типов чисел:
| Тип числа | Пример |
|---|---|
| Натуральное число | 5 |
| Целое число | -2 |
| Рациональное число | 3/4 |
| Иррациональное число | √3 |
| Трансцендентное число | π (пи) |
Знание различных типов чисел позволяет нам лучше понимать мир вокруг нас и применять их в реальных ситуациях. Они играют важную роль в математике и других науках, а также в повседневной жизни.
Римские цифры
Символы и их значения:
- I (1): это самый маленький символ, который может быть использован одиночно или в сочетании с другими символами. Например, III = 3, IV = 4.
- V (5): этот символ может быть использован в сочетании с I для обозначения чисел от 6 до 8. Например, VI=6, VIII=8.
- X (10): этот символ может быть использован в сочетании с I или V для обозначения чисел от 11 до 19. Например, XI=11, XV=15.
- L (50): этот символ может быть использован в сочетании с I, V, X для обозначения чисел от 51 до 89. Например, LX=60, LXXX=80.
- C (100): этот символ может быть использован в сочетании с I, V, X, L для обозначения чисел от 101 до 499. Например, CIX=109, CD=400.
- D (500): этот символ может быть использован в сочетании с I, V, X, L, C для обозначения чисел от 501 до 899. Например, DX=510, DCCC=800.
- M (1000): этот символ может быть использован в сочетании с I, V, X, L, C, D для обозначения чисел от 1001 и выше. Например, MX=1010, MCMXCIX=1999.
Примеры использования римских цифр:
“В Риме огромное значение придавалось числу 1000, которое обозначалось символом M. Например, год 2022 в римской нумерации записывается как MMXXII.”
| Римская цифра | Арабское число |
|---|---|
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Римская система нумерации, использующая символы I, V, X, L, C, D и M, имеет свои особенности и ограничения. Несмотря на то, что она не используется в повседневной жизни, знание римской нумерации может быть полезным для изучения истории и культуры Древнего Рима.
Как дать характеристику числу?
1. Тип числа
Отражает признаки и свойства числа на основе его типа. К числам могут относиться:
- натуральные числа – числа, которыми считаются натуральные от 1 до бесконечности;
- целые числа – числа, включающие натуральные числа, их противоположности и ноль;
- рациональные числа – числа, представимые обыкновенной или десятичной дробью;
- иррациональные числа – числа, не могущие быть представлены дробью;
- вещественные числа – объединяют рациональные и иррациональные числа;
- комплексные числа – числа вида a + bi, где a и b – вещественные числа, i – мнимая единица.
2. Значение числа
Описывает, что обозначает само число:
- положительное число – число, больше нуля;
- отрицательное число – число, меньше нуля;
- нуль – число, которое не имеет значения в отношении к немагативным или наоборот.
3. Разрядность числа
Описывает количество цифр в числе и его расположение в разрядах. Виды разрядов:
- единицы – самый младший разряд числа;
- десятки – второй разряд числа, которым обозначается количество десятков;
- сотни – третий разряд числа, которым обозначается количество сотен;
- тысячи – четвертый разряд числа, которым обозначается количество тысяч;
- миллионы – пятый разряд числа, которым обозначается количество миллионов.
4. Десятичное представление числа
Если число представлено в десятичном виде, его можно охарактеризовать следующими параметрами:
- количество десятичных знаков – количество цифр после десятичной точки;
- наибольшая цифра в числе – самое большое число из присутствующих в нем цифр;
- наименьшая цифра в числе – самое маленькое число из присутствующих в нем цифр.
Давая характеристику числу, можно точно определить его тип, значение, разрядность и десятичное представление. Используя эти параметры, можно более полно и точно описать число и его свойства.
Из чего состоит число
Десятичная система счисления
Мы используем десятичную систему счисления, где числа состоят из десяти различных цифр, обозначаемых символами от 0 до 9. Каждая цифра в числе представляет определенное значение в зависимости от ее позиции.
Позиционная система
Числа в десятичной системе счисления структурированы по позиционной системе, где каждая позиция в числе имеет свое значение. Например, число 348 состоит из трех позиций: сотни (300), десятки (40) и единицы (8).
Цифры
Цифры – это символы, которые используются для представления чисел. В десятичной системе счисления мы используем следующие цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждая цифра может быть использована для формирования числа в сочетании с другими цифрами.
Порядок
В десятичной системе счисления порядок каждой позиции увеличивается в 10 раз по сравнению с предыдущей позицией. Это означает, что каждая цифра в числе имеет свое значение, которое зависит от ее позиции и порядка. Например, в числе 348, сотни имеют порядок 10 2 (100), десятки имеют порядок 10 1 (10), а единицы имеют порядок 10 0 (1).
Разряды
Числа можно разделить на разряды, где каждый разряд представляет определенную позицию в числе. Наиболее распространенные разряды в десятичной системе счисления – это единицы, десятки, сотни, тысячи, миллионы и т. д. Каждый разряд имеет свое значение в зависимости от его позиции относительно других разрядов.
Значение
Значение числа определяется путем сочетания его цифр, их позиций и порядка. Каждая цифра придает числу свое значение, которое определяет его относительную величину. Например, число 348 имеет значение 300 для сотен, 40 для десятков и 8 для единиц.
Отличия числа от цифры
Итак, основные отличия числа от цифры:
- Сущность: число – это абстрактное понятие, которое можно представить в разных формах (например, словесно или символьно), а цифра – это конкретный графический символ, который используется для записи чисел.
- Значение: число имеет математическое значение и может быть использовано в различных операциях (сложение, вычитание, умножение и деление), в то время как цифра представляет определенное значение в рамках данной системы счисления.
- Количество: число может состоять из одной или нескольких цифр, в зависимости от его величины, а цифра сама по себе представляет один отдельный графический символ.
Итак, число и цифра являются взаимосвязанными понятиями, но имеют разные сущностные и функциональные отличия. Понимание этих отличий помогает нам более точно использовать и интерпретировать числовую информацию в нашей повседневной жизни.