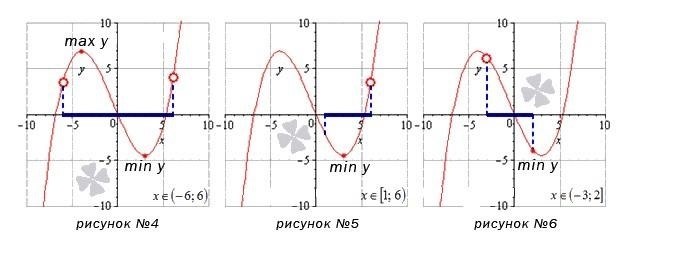
Наименьшее значение функции – это значение, которое является наименьшим среди всех возможных значений, принимаемых функцией на заданном промежутке. Для нахождения наименьшего значения функции необходимо использовать методы математического анализа, такие как нахождение производной функции и решение уравнения на её нули, или применение методов оптимизации. Одним из таких методов является метод дихотомии, который позволяет приближенно найти наименьшее значение функции на заданном интервале. Все эти методы позволяют найти точку, в которой функция достигает своего наименьшего значения, что является важным инструментом в решении различных математических и инженерных задач.
Как записать, каким символом обозначают
1. Математические операции и символы
Для обозначения различных математических операций используются специальные символы:
- + – обозначает сложение;
- – – обозначает вычитание;
- * – обозначает умножение;
- / – обозначает деление;
- = – обозначает равенство;
- > – обозначает больше;
- < – обозначает меньше;
- ≤ – обозначает меньше или равно;
- ≥ – обозначает больше или равно;
- + – обозначает плюс-минус;
- ! – обозначает факториал;
2. Символы для записи формул и выражений
При записи формул и выражений также используется специальные символы:
- x – обозначает переменную;
- y – обозначает другую переменную;
- a, b, c – обозначают коэффициенты;
- n – обозначает степень;
- ∑ – обозначает сумму;
- π – обозначает число Пи;
- ∞ – обозначает бесконечность;
- +, –, *, /, (, ) – используются для группировки и организации операций.
3. Символы для обозначения логических операций
Для записи логических операций, таких как “И”, “ИЛИ”, “НЕ”, используются следующие символы:
- ∧ – обозначает логическое “И”;
- ∨ – обозначает логическое “ИЛИ”;
- ¬ – обозначает логическое “НЕ”.
4. Символы для записи множеств и отношений
Для записи множеств и отношений используются различные символы:
- {} – обозначает множество;
- ∈ – обозначает “принадлежит”;
- ∉ – обозначает “не принадлежит”;
- ⊂ – обозначает “подмножество”;
- ⊆ – обозначает “подмножество или равно”;
- ∪ – обозначает “объединение множеств”;
- ∩ – обозначает “пересечение множеств”.
5. Пример использования символов
Давайте рассмотрим пример, в котором используются различные символы:
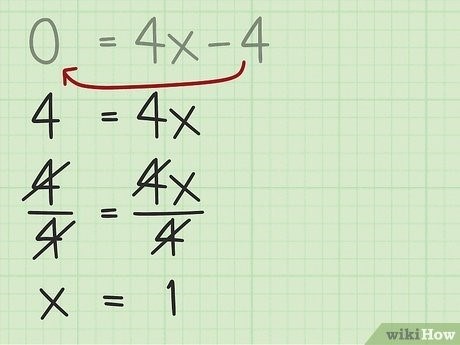
| Формула | Нотация |
|---|---|
| Квадратный корень из 4 | √4 = 2 |
| Сумма чисел от 1 до 10 | ∑i=110 i = 55 |
| Множество всех целых чисел | ℤ = {…, -3, -2, -1, 0, 1, 2, 3, …} |
Знание правильной нотации при записи математических операций и символов является важным навыком, который поможет вам в понимании и коммуникации в различных областях, связанных с математикой и информатикой.
Об этой статье
В данной статье мы изучили, как найти наименьшее значение функции. Мы рассмотрели два метода: метод дифференцирования и метод исследования функции на возрастание и убывание.
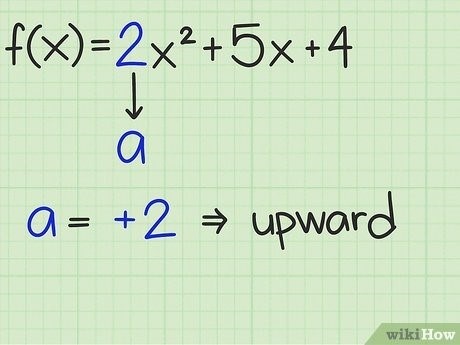
Метод дифференцирования позволяет найти точку экстремума функции, которая может быть как наименьшим значением, так и наибольшим. Для этого необходимо найти производную функции, приравнять ее к нулю и решить полученное уравнение. Затем нужно проверить, является ли найденная точка минимумом или максимумом, например, с помощью знака второй производной.
Метод исследования функции на возрастание и убывание состоит в анализе знака первой производной функции на заданном интервале. Если производная положительна, то функция возрастает, если отрицательна – убывает. Если производная меняет знак с плюса на минус, то функция имеет локальный максимум; с минуса на плюс – локальный минимум. Таким образом, наименьшее значение функции будет соответствовать ее локальному минимуму.
В данной статье мы рассмотрели оба метода на примере конкретных функций и предоставили шаги по их применению. Надеемся, что эта информация окажется полезной и поможет вам найти наименьшее значение функции в дальнейших математических исследованиях.