Операция нахождения производной называется дифференцированием. Дифференцирование является одной из основных операций математического анализа и позволяет находить скорость изменения функции в каждой точке ее области определения. Оно применяется в различных областях науки, техники и экономики для решения задач, связанных с изменениями и зависимостями.
Правила нахождения производных
Определение производной
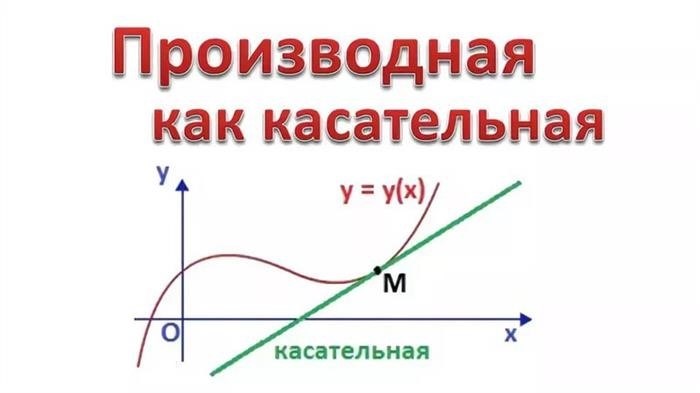
Производная функции отображает скорость изменения значения функции в зависимости от изменения ее аргумента. Можно рассматривать производную как коэффициент наклона касательной к графику функции в заданной точке. В математической нотации производную функции обозначают символом f'(x) или dy/dx.
Основные правила нахождения производных
-
Правило константы: Производная константы равна нулю.
-
Правило степенной функции: Производная степенной функции равна произведению степени функции на производную ее аргумента.

-
Правило суммы: Производная суммы двух функций равна сумме их производных.
-
Правило произведения: Производная произведения двух функций равна произведению первой функции на производную второй функции, плюс произведение второй функции на производную первой функции.
-
Правило частного: Производная частного двух функций равна разности произведения первой функции на производную второй функции и произведения второй функции на производную первой функции, деленной на квадрат второй функции.
Применение правил нахождения производных
Правила нахождения производных широко применяются в различных областях для анализа функций и решения задач. Они позволяют определить экстремумы функций, найти параметры, при которых функция достигает максимума или минимума, и многое другое. Производные также используются для построения моделей, предсказания трендов и оптимизации процессов в различных сферах деятельности.
Постоянное обновление знаний о производных
Правила нахождения производных требуют от математиков и практикующих специалистов постоянного обновления знаний и навыков. Постановка задач, нахождение аналитических решений и интерпретация результатов требуют точности и аккуратности в применении правил. Обучение и практика позволяют развивать интуицию и уверенность в использовании производных для анализа и оптимизации процессов.
Геометрический и физический смысл производной
Геометрический смысл производной:
Геометрический смысл производной связан с изучением изменений функции на графике. Производная определяет тангенс угла наклона касательной к графику функции в заданной точке. В геометрическом смысле производная показывает, насколько быстро функция изменяется при изменении аргумента.
Пример: Пусть имеется график функции, описывающей движение тела по прямой. Значение производной в каждой точке говорит о скорости изменения положения тела в данной точке. Если производная положительна, то тело движется в положительном направлении оси, если отрицательна – в отрицательном направлении. Если производная равна нулю, то тело находится в покое.
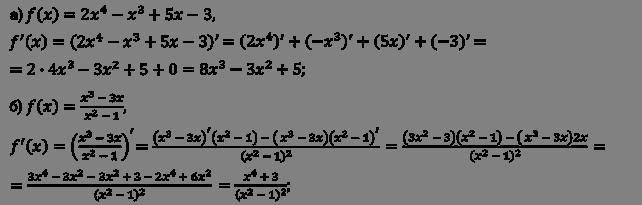
Физический смысл производной:
Физический смысл производной связан с динамическими явлениями в физике. Он позволяет описать зависимость различных физических величин от времени или других переменных. Производная указывает на изменение этих величин с течением времени.
Пример: В физике производная описывает скорость изменения времени, а значит, скорость изменения скорости, т.е. ускорение. Если производная положительна, то объект ускоряется, если отрицательна – замедляется. Производная позволяет описать законы движения, эффективность процессов и другие физические явления.
Применение производной в геометрии и физике:
- Нахождение касательных к кривым.
- Определение точек экстремума функции (минимумы и максимумы).
- Исследование оптических систем и зеркал.
- Описание процессов изменения физических величин во времени.
- Анализ скорости и ускорения объектов в физических задачах.
Геометрический и физический смысл производной позволяют понять ее значение и применение в различных областях наук. Геометрический смысл производной связан с изучением графиков функций и определением их изменений. Физический смысл производной используется в физических задачах для описания динамических процессов и изменения различных величин во времени. Производная играет важную роль в анализе, предсказании и оптимизации различных явлений и процессов.
Таблица производных простых функций
Таблица производных простых функций содержит список производных основных элементарных функций. За их помощью можно получить значения производных более сложных функций. Знание этой таблицы позволяет быстро и удобно находить производную для большинства простых функций.
Основные правила дифференцирования
- Линейность производной: производная суммы равна сумме производных, производная произведения равна произведению производных, производная частного равна частному производных.
- Производная константы равна нулю.
- Производная степенной функции равна произведению степени функции на производную основы.
- Производная экспоненты равна экспоненте умноженной на производную показателя степени.
- Производная логарифма равна производной аргумента, деленной на значение функции.
Таблица производных
| Функция | Производная |
|---|---|
| f(x) = C (где C – константа) | f'(x) = 0 |
| f(x) = x n (где n – целое число) | f'(x) = n*x (n-1) |
| f(x) = e x (e – основание натурального логарифма) | f'(x) = e x |
| f(x) = ln(x) (x – положительное число) | f'(x) = 1/x |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
| f(x) = tan(x) | f'(x) = sec 2(x) |
Таблица производных простых функций является полезным инструментом для быстрого нахождения производных и применения их в различных математических и инженерных расчетах. Знание этих производных позволяет экономить время при анализе функций и решении задач, где требуется вычисление производных.
Курсовые работы, написанные опытными преподавателями ВУЗов
Преимущества написания курсовых работ опытными преподавателями
- Глубокие знания и опыт: Действующие преподаватели ВУЗов обладают высокой квалификацией и глубокими знаниями в своей предметной области. Они имеют практический опыт в области научных исследований и, следовательно, могут предложить студенту актуальные и интересные темы для курсовой работы.
- Индивидуальный подход: Каждый студент имеет свои особенности и потребности. Преподаватели, работающие в ВУЗах, способны оценить индивидуальные особенности каждого студента и предложить ему подходящую тему для курсовой работы.
- Качество и достоверность: Преподаватели ВУЗов знакомы с требованиями и стандартами оформления курсовых работ и могут гарантировать высокое качество и достоверность написания.
- Своевременное выполнение: Преподаватели ВУЗов знают, как важно придерживаться сроков сдачи курсовых работ. Они обеспечивают своевременное выполнение работы и помогают студентам избежать проблем с сдачей.
- Конфиденциальность: Преподаватели ВУЗов гарантируют конфиденциальность и сохранение личной информации студентов. Они не разглашают никакую информацию о процессе написания курсовой работы.
Описание процесса написания курсовой работы преподавателями ВУЗов
Процесс написания курсовой работы преподавателями ВУЗов включает следующие этапы:
- Выбор темы. Преподаватель предлагает студенту несколько вариантов тем для курсовой работы, учитывая его академические интересы и специализацию.
- Подготовка плана. Преподаватель помогает студенту разработать план курсовой работы, определить основные разделы и подразделы.
- Сбор информации. Преподаватель рекомендует студенту источники информации для написания курсовой работы, помогает в поиске и анализе необходимых данных.
- Оформление работы. Преподаватель проверяет оформление работы в соответствии с требованиями ВУЗа и научной методики. Он осуществляет редактирование ошибок, проверяет правильность цитирования и приведения ссылок.
- Контроль качества. Преподаватель осуществляет последующую проверку работы на качество и достоверность научного изложения, а также на соответствие заданным требованиям.
- Финальное сопровождение. Преподаватель сопровождает студента в процессе защиты курсовой работы, отвечая на вопросы и помогая в подготовке презентации.
Таким образом, написание курсовой работы опытными преподавателями ВУЗов обеспечивает студентам профессиональную помощь, качественное выполнение работы и достижение хороших результатов.
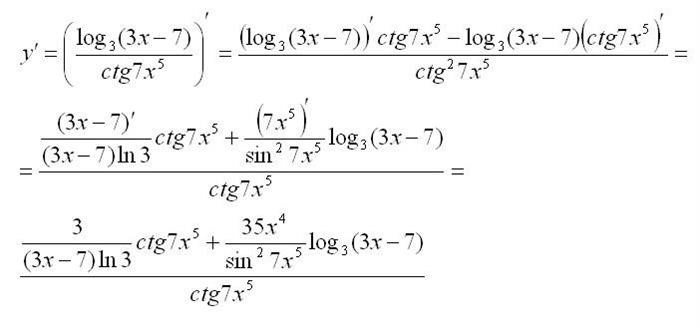
Продолжаем искать производные вместе
Процесс нахождения производной требует понимания концепции предела и правил дифференцирования. Приведем несколько методов и правил, которые помогут нам найти производные различных функций.
Методы нахождения производной
В нашем изучении производных мы используем несколько методов:
- Метод множителей Лагранжа;
- Метод дифференцирования по формуле Лейбница;
- Метод последовательного дифференцирования;
- Метод использования определения производной.
Правила дифференцирования
Для удобства нахождения производной различных функций существуют определенные правила:
- Правило суммы и разности;
- Правило произведения;
- Правило частного;
- Правило цепной дифференциации;
- Правило обратной функции;
- Правило экспоненты и логарифма;
- Правило степени.
Примеры нахождения производных
Рассмотрим несколько примеров, чтобы лучше понять процесс нахождения производной. Задачи могут быть различной сложности, включая функции с использованием тригонометрических и логарифмических функций.
| Пример | Функция | Производная |
|---|---|---|
| Пример 1 | f(x) = x 2 + 3x | f'(x) = 2x + 3 |
| Пример 2 | f(x) = sin(x) + cos(x) | f'(x) = cos(x) – sin(x) |
| Пример 3 | f(x) = ln(x) / x | f'(x) = (-ln(x) + 1) / x 2 |
Таким образом, изучение производных – это интересный и важный процесс, который помогает нам понять скорость изменения функций. Применение различных методов и правил дифференцирования позволяет нам находить производные различных функций. Надеюсь, эти примеры помогут вам лучше понять процесс нахождения производной и дадут вам уверенность в работе с этой важной математической операцией.
Пошаговые примеры – как найти производную
Пример 1: Простое дифференцирование
Простое дифференцирование используется для нахождения производной для функций, содержащих только одну переменную.
Допустим, у нас есть функция f(x) = 3x 2. Чтобы найти производную этой функции, нужно умножить показатель степени на коэффициент и уменьшить показатель степени на 1. В нашем случае:
f'(x) = 2 * 3 * x (2 – 1) = 6x
Пример 2: Правила дифференцирования элементарных функций
Правила дифференцирования элементарных функций позволяют находить производные для функций, содержащих элементарные функции, такие как синус, косинус, тангенс и другие.
Допустим, у нас есть функция f(x) = sin(x). Чтобы найти производную этой функции, нужно применить правило дифференцирования для синуса, которое гласит: производная синуса равна косинусу.
f'(x) = cos(x)
Пример 3: Логарифмическое и экспоненциальное дифференцирование
Дифференцирование логарифмических и экспоненциальных функций может быть сложным. Для нахождения производных таких функций применяются специальные правила и формулы.
Допустим, у нас есть функция f(x) = ln(x). Чтобы найти производную этой функции, нужно применить правило дифференцирования для натурального логарифма, которое гласит: производная натурального логарифма равна 1/x.
f'(x) = 1/x
- Простое дифференцирование позволяет находить производные для функций с одной переменной.
- Правила дифференцирования элементарных функций применяются для функций, содержащих элементарные функции.
- Логарифмическое и экспоненциальное дифференцирование используется для функций с логарифмами и экспонентами.
Нахождение производной является важной задачей в математике и имеет множество применений в физике, экономике, инженерии и других областях. Понимание основных методов и правил дифференцирования позволяет более точно анализировать изменения величин и прогнозировать результаты.
Дифференциальное исчисление функций одной переменной
В данной статье мы рассмотрели основные понятия и принципы дифференциального исчисления функций одной переменной. Начав с определения производной и приведения формулы для ее вычисления, мы разобрались с основными правилами дифференцирования функций.
Используя эти правила, мы можем находить производные различных функций, а также применять их для решения различных задач. Например, производная позволяет определить точку экстремума функции, а также скорость изменения значения функции в данной точке.
Дифференциальное исчисление имеет широкое применение в различных областях науки и техники, где требуется анализ изменения функций по их переменным. Оно является одной из важнейших математических дисциплин, позволяющих предсказывать и описывать физические, экономические и другие явления.
Используя знания о дифференцировании функций, мы можем более глубоко понять и анализировать поведение и свойства функций и использовать их для решения сложных задач. Важно помнить, что дифференциальное исчисление – это лишь часть более обширной области математического анализа, которая включает в себя и другие многообразные методы и приемы.