В стереометрии основными фигурами являются трехмерные плоские геометрические тела, которые имеют объем и форму. К таким фигурам относятся такие объекты, как сферы, конусы, цилиндры, параллелепипеды, пирамиды и другие. Каждая фигура имеет свои характерные особенности и свойства, которые определяют ее визуальный образ и применение в различных областях науки, инженерии и дизайне.
Базовые теоремы, аксиомы и определения стереометрии
Основные определения
- Точка – основной элемент стереометрии, не имеющий размеров и обозначаемый буквой. Точка может быть задана координатами или с помощью геометрического описания.
- Прямая – множество точек, которые лежат на одной прямой линии и не имеют размеров. Прямая обозначается одной буквой или двумя точками на ней.
- Отрезок – часть прямой, ограниченная двумя точками на ней. Отрезок имеет длину и обозначается двумя точками на прямой.
- Плоскость – множество точек, образующих плоскую поверхность. Плоскость может быть задана с помощью точки и нормали к плоскости или тремя точками на плоскости.
- Треугольник – фигура, образованная тремя отрезками, соединяющими три точки. Треугольник имеет три стороны, три угла и обозначается тремя точками на плоскости.
- Параллелограмм – четырехугольник, у которого противоположные стороны равны и параллельны друг другу.
- Цилиндр – трехмерная фигура, образованная двумя параллельными плоскостями, называемыми основаниями, и боковой поверхностью, которая представляет собой прямоугольник, обернутый вокруг осей, соединяющих основания.
Базовые теоремы и аксиомы
- Теорема Пифагора – в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
- Теорема о сумме углов треугольника – сумма углов треугольника равна 180 градусам.
- Аксиома параллельных прямых – через точку, не лежащую на данной прямой, проходит ровно одна прямая, параллельная данной.
- Теорема о площади прямоугольного параллелепипеда – площадь боковой поверхности прямоугольного параллелепипеда равна произведению периметра основания на высоту.
- Теорема о площади поверхности цилиндра – площадь боковой поверхности целиндра равна произведению окружности основания на высоту цилиндра.
Основные стереометрические фигуры
Первой фигурой, которую мы изучили, была параллелепипед. Он имеет шесть граней, которые являются прямоугольниками, и все углы прямые. Параллелепипед широко применяется в архитектуре и строительстве.
Далее мы рассмотрели пирамиду. Пирамида имеет много граней, одна из которых является основанием, а остальные сходятся в одной точке, называемой вершиной. Пирамида имеет различные формы и может быть треугольной, четырехугольной и так далее.
Также важной фигурой является цилиндр. Цилиндр имеет две круглые грани, называемые основаниями, и боковую поверхность, которая состоит из криволинейного тела. Цилиндр часто встречается в повседневной жизни, например, в форме банок и бутылок.
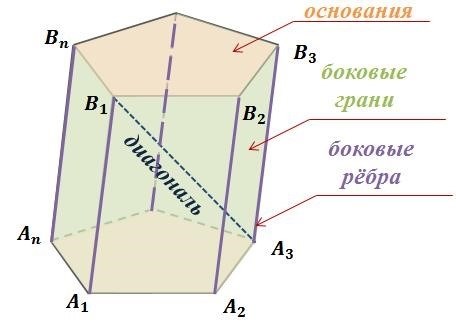
И, наконец, мы изучили шар. Шар – это фигура, которая полностью закрыта поверхностью и не имеет граней и ребер. Он имеет одну грань – сферу. Шар широко используется в математике, физике и других науках.

Все эти фигуры имеют различные свойства и характеристики. Они играют важную роль в геометрии и имеют множество применений в реальном мире.