Определение наибольшего и наименьшего значения функции на определенном отрезке является важным аспектом в анализе функций. Для нахождения этих значений необходимо применять различные методы и инструменты, такие как производные, графики функций, экстремумы и другие математические концепции. Знание этих методов поможет определить максимальное и минимальное значение функции на отрезке и применить их в различных областях, таких как оптимизация, экономика и физика.
Общая схема исследования функций и построения графиков
1. Определение области определения функции
Первым шагом при исследовании функции является определение ее области определения. Область определения – это множество значений аргументов, для которых функция имеет смысл. Для этого необходимо изучить все ограничения на аргументы функции, такие как корни в знаменателе или логарифмы с отрицательными аргументами.
2. Определение особых точек
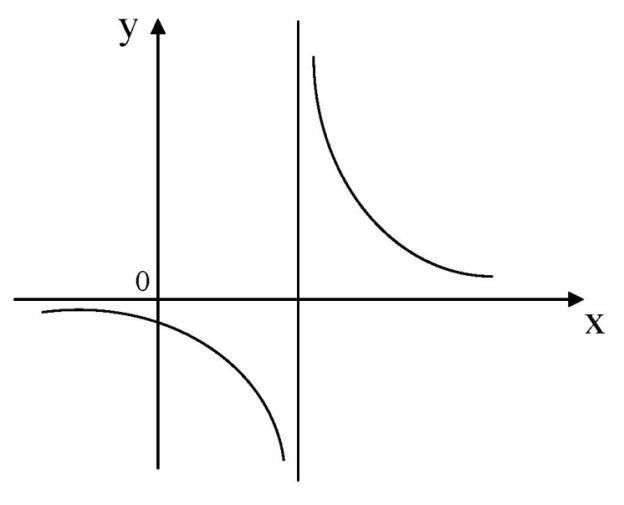
Особые точки – это точки, в которых функция имеет особые свойства, такие как разрывы, вертикальные асимптоты, точки перегиба и экстремумы. Для определения особых точек необходимо найти значения аргументов, при которых функция может изменять свое поведение или иметь критические точки.
3. Анализ поведения функции на интервалах
После определения особых точек необходимо проанализировать поведение функции на каждом из интервалов, образованных особыми точками. Для этого надо выяснить, возрастает или убывает функция на каждом интервале, определить наличие экстремумов и точек перегиба.
4. Нахождение точек пересечения с осями координат
Далее следует найти точки пересечения графика функции с осями координат. Для этого необходимо найти значения аргументов, при которых функция принимает нулевые значения или делится на ноль.
5. Построение графика функции
И, наконец, после проведения анализа и нахождения всех необходимых точек, можно приступить к построению графика функции. Для этого используется координатная плоскость, на которой отображаются все рассчитанные значения функции и точки особых свойств.
Асимптоты графика функции. Исследование функции на асимптоты
Что такое асимптота?
Асимптота графика функции – это прямая, к которой график стремится на бесконечности или в какой-то момент останавливается. Асимптоты могут быть вертикальными, горизонтальными или наклонными.
Как найти асимптоты графика функции?
Исследование функции на асимптоты требует выполнения нескольких шагов:
- Найти вертикальные асимптоты – это значения x, при которых функция стремится к бесконечности или принимает одно из особых значений, таких как 0 или бесконечность.
- Найти горизонтальные асимптоты – это значения y, к которым функция стремится на бесконечности. Для этого нужно рассмотреть предел функции при x, стремящемся к бесконечности.
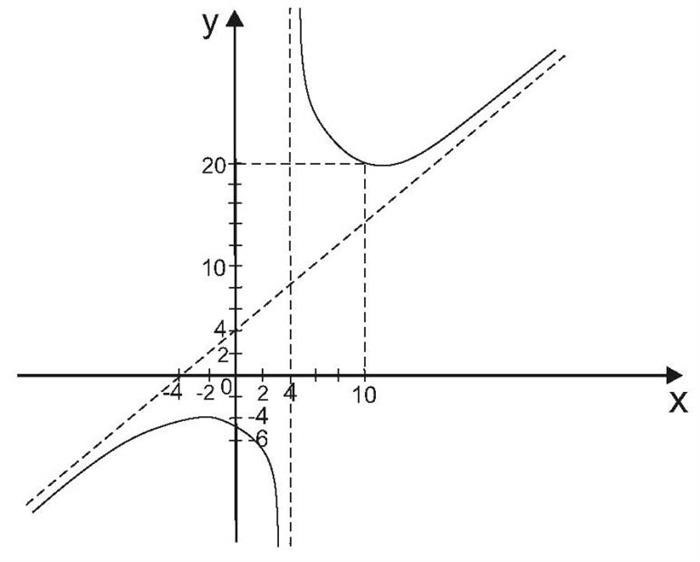
- Найти наклонные асимптоты – это прямые, к которым график функции приближается на бесконечности, но не совпадает с ними. Для этого нужно рассмотреть предел функции при x, стремящемся к бесконечности, и приблизить его уравнением прямой.
Пример исследования функции на асимптоты
Рассмотрим функцию f(x) = 2x / (x – 1). Исследуем ее на асимптоты.
- Вертикальная асимптота: при x = 1 функция не определена, поэтому график стремится к бесконечности при x = 1.
- Горизонтальная асимптота: рассмотрим предел функции при x, стремящемся к бесконечности. Если предел существует, то он является горизонтальной асимптотой. В данном случае предел равен 2, поэтому уравнение горизонтальной асимптоты будет y = 2.
- Наклонная асимптота: рассмотрим предел функции при x, стремящемся к бесконечности. Если предельное значение отлично от бесконечности или конечного числа, то асимптота наклонная. В данном случае предел не существует, поэтому наклонной асимптоты нет.
Таким образом, график функции f(x) = 2x / (x – 1) имеет вертикальную асимптоту x = 1 и горизонтальную асимптоту y = 2.
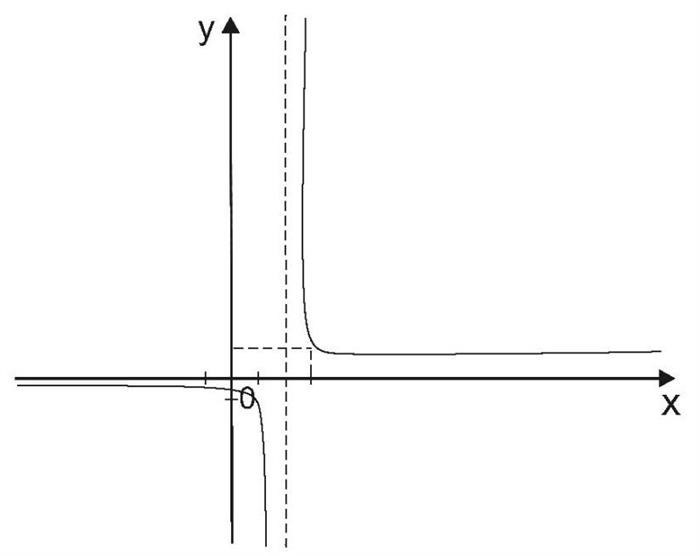
Асимптоты графика функции дают нам информацию о его поведении на бесконечности и позволяют лучше понять особенности графика. При исследовании функции на асимптоты необходимо найти вертикальные, горизонтальные и наклонные асимптоты, учитывая пределы функции на бесконечности.
Исследование функции на выпуклость и точку перегиба
Для исследования функции на выпуклость необходимо найти вторую производную и выяснить знак этой производной на заданном отрезке. Если вторая производная положительна, то функция является выпуклой на этом отрезке. Если вторая производная отрицательна, то функция вогнута на данном отрезке.
Точка перегиба – это точка, в которой выпуклость функции меняется. На отрезке может быть несколько точек перегиба. Чтобы найти точку перегиба, необходимо приравнять вторую производную к нулю и найти ее корни. Затем следует проанализировать знак второй производной в окрестности корней, чтобы определить, является ли точка перегиба точкой максимума или минимума.
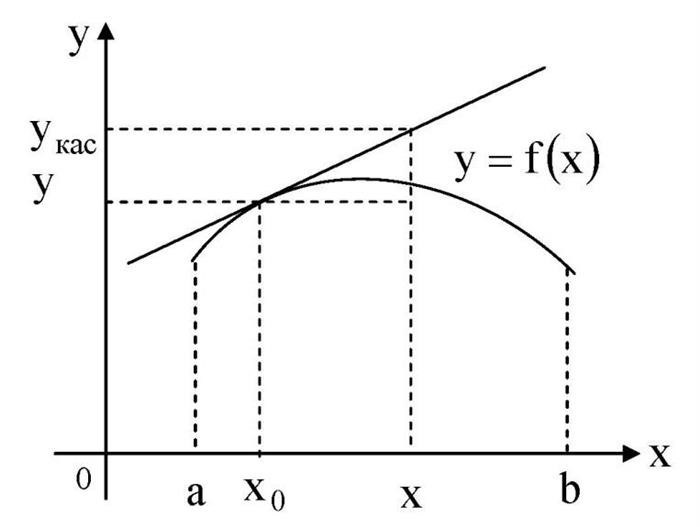
Итак, при исследовании функции на выпуклость и точку перегиба необходимо выполнить следующие шаги: