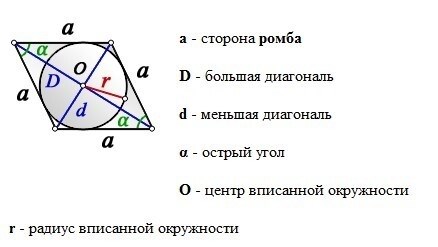
В геометрии существуют две основные формулы, связанные с окружностями: формула описанной окружности и формула вписанной окружности. Формула описанной окружности позволяет найти радиус окружности, в которую вписан треугольник или многоугольник, а формула вписанной окружности помогает найти радиус окружности, которая касается всех сторон треугольника или многоугольника. Использование этих формул облегчает решение задач по геометрии и помогает определить свойства фигур.
Радиус и диаметр
Радиус – это расстояние от центра окружности до любой ее точки. Обозначается обычно буквой “r”. Радиус является постоянным для данной окружности и одинаков для всех точек, лежащих на окружности.
Диаметр – это наибольшее расстояние между двумя точками на окружности, проходящими через ее центр. Обозначается обычно буквой “d”. Диаметр в два раза больше радиуса и является двумерной характеристикой окружности.
Различия между радиусом и диаметром:
- Радиус – это расстояние от центра окружности до ее точки, а диаметр – наибольшее расстояние между двумя точками на окружности, проходящими через ее центр.
- Диаметр в два раза больше радиуса.
- Радиус обозначается буквой “r”, а диаметр обозначается буквой “d”.
Связь между радиусом и диаметром:
Радиус и диаметр взаимосвязаны следующим образом:
- Радиус равен половине диаметра: r = d / 2.
- Диаметр равен удвоенному радиусу: d = 2r.
Примеры использования радиуса и диаметра:
| Пример | Описание |
|---|---|
| Расчет площади окружности | Площадь окружности можно вычислить с помощью формулы: S = πr², где “S” – площадь, “π” – математическая константа (приближенное значение равно 3.14159), “r” – радиус. |
| Расчет длины окружности | Длину окружности можно вычислить с помощью формулы: C = 2πr, где “C” – длина окружности, “π” – математическая константа (приближенное значение равно 3.14159), “r” – радиус. |
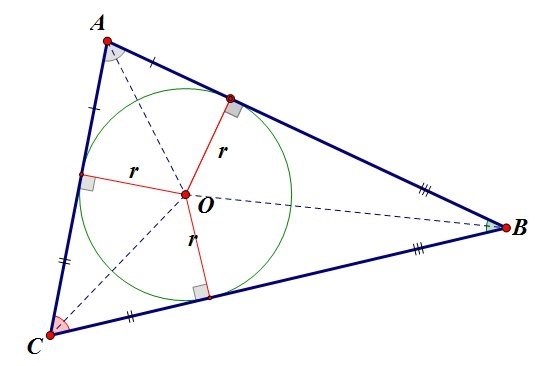
| Построение вписанной окружности | Вписанная окружность – это окружность, которая касается каждой стороны многоугольника. Радиус вписанной окружности является половиной длины отрезка, соединяющего вершину многоугольника и центр окружности. |
| Построение описанной окружности | Описанная окружность – это окружность, которая проходит через каждую вершину многоугольника. Радиус описанной окружности является расстоянием от центра окружности до вершины многоугольника. |
Радиус и диаметр – основные характеристики окружности, которые широко используются в математике, геометрии и других областях. Радиус – это расстояние от центра окружности до точек на ней, а диаметр – наибольшее расстояние между двумя точками на окружности, проходящими через ее центр. Радиус и диаметр взаимосвязаны и используются для решения различных задач, таких как расчет площади и длины окружности, а также построение вписанных и описанных окружностей.
Что такое радиус?
Ниже представлены основные характеристики радиуса:
- Длина радиуса: радиус измеряется в линейных единицах и является отрезком прямой, соединяющей центр окружности с ее любой точкой.
- Радиус и диаметр: диаметр окружности равен удвоенному значению радиуса, то есть диаметр равен двум радиусам.
- Радиус и площадь окружности: площадь окружности может быть вычислена по формуле, где радиус является одним из параметров.
Известные формулы, связанные с радиусом:
- Длина окружности: длина окружности равна удвоенному значению числа π, умноженному на радиус.
- Площадь окружности: площадь окружности равна произведению числа π на квадрат радиуса.
Радиус играет важную роль при решении геометрических задач и конструировании различных фигур. Зная радиус, можно определить длину окружности, площадь и другие параметры окружности.
| Формула | Описание |
|---|---|
| Длина окружности | Длина окружности равна удвоенному значению числа π, умноженному на радиус. |
| Площадь окружности | Площадь окружности равна произведению числа π на квадрат радиуса. |
Примеры использования радиуса:
- При расчете площади круглого стола, зная радиус, можно применить соответствующую формулу и получить точное значение площади.
- При построении фигуры с вписанной окружностью, радиус определяет местоположение и размеры окружности внутри фигуры.
Познайте геометрический мир с помощью радиуса – ключевого параметра для описания и вписывания окружностей!
Была ли вам полезна статья?
В данной статье мы рассмотрели различные формулы и свойства описанной и вписанной окружностей. Надеемся, что информация, представленная в статье, была полезной для вас и помогла разобраться в этой теме.
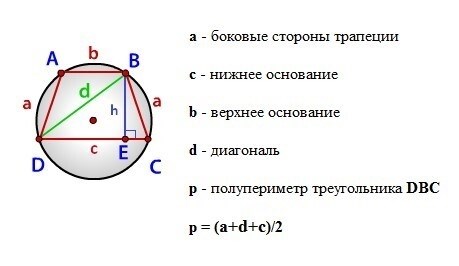
Описанные нами формулы и свойства могут быть применены в решении задач по геометрии, а также могут быть полезны при изучении и понимании других математических тем, связанных с окружностями.
Чтобы лучше усвоить материал, рекомендуем повторить основные понятия, примеры и формулы, представленные в статье. Также рекомендуем решить несколько задач на применение данных формул и свойств.
Мы надеемся, что данная статья помогла вам расширить ваше понимание описанной и вписанной окружностей, и вы сможете успешно применять полученные знания при решении геометрических задач. Удачи в вашем учебном процессе и дальнейших исследованиях в области геометрии!