Множество значений функции – это набор всех возможных результатов, которые могут быть получены при подстановке различных значений аргумента в функцию. Оно определяется и зависит от самой функции, ее аргументов и области, в которой она определена.
2 Билет: простейшие преобразования графика функции
1. График функции и его основные элементы
График функции представляет собой множество точек, координаты которых соответствуют значениям функции. Элементы графика функции:
- Точки графика – точки, представляющие значения функции;
- Оси координат – вертикальная и горизонтальная оси, на которых отображаются значения аргумента и функции;
- Единицы измерения – шкалы на осях, позволяющие определить значения аргумента и функции;
- Надписи – подписи осей, название функции и другие сопутствующие текстовые элементы.
2. Преобразования графика функции
Преобразования графика функции позволяют изменить его положение, масштабность, форму и другие характеристики. Рассмотрим основные простейшие преобразования:
2.1. Сдвиг графика вдоль осей координат
Сдвиг графика функции вдоль осей координат выполняется путем прибавления или вычитания определенных значений из аргумента и функции. Например, сдвиг графика функции y = f(x) вправо на 2 единицы будет выглядеть как y = f(x – 2), а сдвиг влево на 3 единицы – как y = f(x + 3).

2.2. Растяжение и сжатие графика вдоль осей координат
Растяжение и сжатие графика функции вдоль осей координат происходит путем умножения или деления значения аргумента и функции на определенные коэффициенты. Например, растяжение графика функции y = f(x) по оси x в 2 раза будет выглядеть как y = f(2x), а сжатие в 0.5 раза – как y = f(0.5x).
2.3. Отражение графика относительно осей координат
Отражение графика функции относительно осей координат – это зеркальное отражение графика относительно вертикальной или горизонтальной оси. Для выполнения отражения достаточно изменить знаки аргумента или функции. Например, отражение графика функции y = f(x) относительно оси x будет выглядеть как y = -f(x), а относительно оси y – как y = f(-x).
2.4. Поворот графика вокруг начала координат
Поворот графика функции вокруг начала координат происходит путем замены аргумента и функции определенными формулами. Например, поворот графика функции y = f(x) на 90 градусов против часовой стрелки будет выглядеть как y = f(-y).
Применение различных преобразований позволяет изменить форму и положение графика функции, анализировать его особенности и свойства. Понимание этих преобразований является важным для изучения и решения задач в области математики и науки в целом.
Об этой статье
Определение множества значений функции
Множество значений функции – это множество всех возможных значений, которые могут быть получены в результате применения функции к различным аргументам. Оно может быть ограниченным или неограниченным, конечным или бесконечным.
Например, если у нас есть функция f(x), то множество значений функции будет обозначаться как f(x) ∈ Y, где Y – это множество значений. Или можно записать как f: X → Y, где X – это множество аргументов, а Y – это множество значений.

Примеры множеств значений функций
Давайте рассмотрим несколько примеров, чтобы лучше понять, что такое множество значений функции:
- Функция f(x) = x 2 имеет множество значений [0, +∞), то есть все неотрицательные числа и плюс бесконечность.
- Функция f(x) = sin(x) имеет множество значений [-1, 1], то есть все значения от -1 до 1 включительно.
- Функция f(x) = 1/x имеет множество значений (-∞, 0) ∪ (0, +∞), то есть все отрицательные числа и все положительные числа.
Свойства множества значений функции
Множество значений функции может иметь различные свойства:
- Ограниченность: множество значений может быть ограниченным сверху, ограниченным снизу или ограниченным как сверху, так и снизу.
- Конечность: множество значений может быть конечным, то есть содержать только конечное число элементов, или бесконечным, то есть содержать бесконечное число элементов.
Множество значений функции играет важную роль в математике, так как оно описывает все возможные значения, которые может принимать функция. Понимание этого понятия позволяет более глубоко изучать и анализировать математические функции.

Связь множества значений функции с областью определения
Множество значений функции и область определения тесно связаны друг с другом и описывают разные аспекты функции. Область определения функции определяет множество всех исходных значений, на которых функция определена, то есть значения, для которых функция дает определенный результат. Множество значений функции, с другой стороны, определяет множество всех возможных результатов функции при заданных значениях в области определения.
Область определения функции определяет, какие значения могут быть входными аргументами функции, а множество значений функции показывает, какие значения могут быть выходными результатами функции. Область определения и множество значений могут быть ограничены некоторыми условиями или ограничениями на входные значения.
В общем случае, область определения функции может быть шире или узкой, чем множество значений функции. Может быть случай, когда область определения функции ограничена определенными значениями, но множество значений функции может быть расширено или иметь большее количество значений. В этом случае функция может иметь несколько значений для одного и того же аргумента или быть необратимой, когда для некоторых аргументов не существует соответствующего значения в области определения.
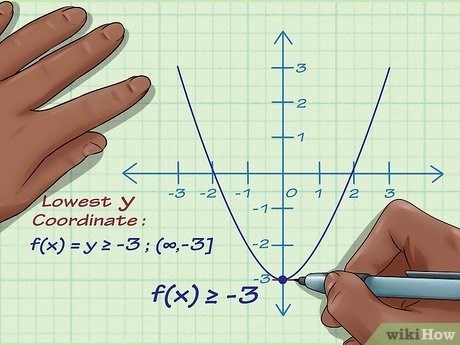
Таким образом, множество значений функции зависит от области определения функции, и оба эти понятия нужно учитывать при изучении и анализе функций.