Функция – это математическое соответствие, которое ставит в соответствие каждому элементу из одного множества элемент из другого множества. График функции – это графическое представление её значений. В данной статье мы рассмотрим различные типы функций, их свойства и графики.
Способы задания функции
Аналитический способ
Аналитический способ задания функции основан на использовании аналитического выражения в виде алгебраической формулы или уравнения. Можно использовать математические операции, специальные символы и переменные, чтобы описать функцию. Например, функция может быть задана как:
- полиномиальное уравнение: f(x) = ax 2 + bx + c
- рациональная функция: f(x) = (ax + b) / (cx + d)
- тригонометрическая функция: f(x) = sin(x)
Табличный способ
Табличный способ задания функции основан на представлении функции в виде таблицы значений. В таблице указываются значения аргумента и соответствующие им значения функции. Множество значений аргумента может быть равномерно распределено или иметь разные интервалы. Пример таблицы для функции может выглядеть следующим образом:
| Аргумент (x) | Значение функции (f(x)) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
Графический способ
Графический способ задания функции основан на построении графика функции. График представляет собой точки на координатной плоскости, где по горизонтальной оси откладываются значения аргумента, а по вертикальной оси – значение функции. График может быть построен вручную или с помощью специальных программ и приборов. Пример графика для функции может выглядеть следующим образом:
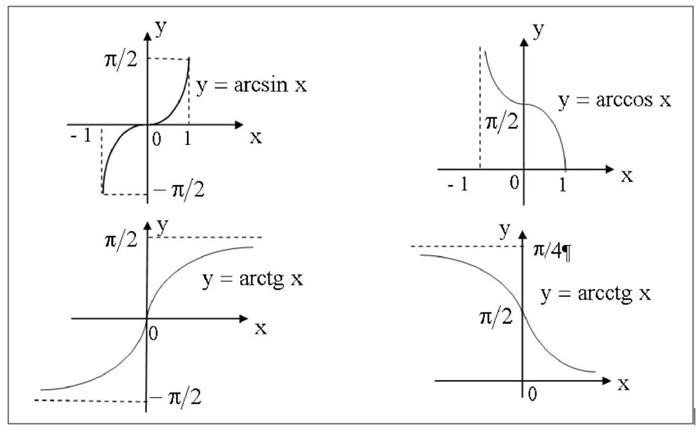
Словесный способ
Словесный способ задания функции основан на описании ее свойств и особенностей в словесной форме. В текстовом описании указываются условия и правила, по которым функция определяется и работает. Например, функцию можно описать таким образом: “Функция f(x) равна квадрату аргумента x”.
Пример исследования и построения функции
В данном примере рассмотрим исследование и построение функции f(x) на отрезке [a, b].
1. Изучение области определения функции:
- Проверяем, нет ли делителя нуля в знаменателе;
- Рассматриваем значения, при которых функция может иметь разрывы.
2. Анализ поведения функции на концах отрезка [a, b]:
- Проверяем, являются ли точки a и b экстремумами функции;
- Исследуем пределы функции на границах отрезка.
3. Нахождение производных и анализ экстремумов:
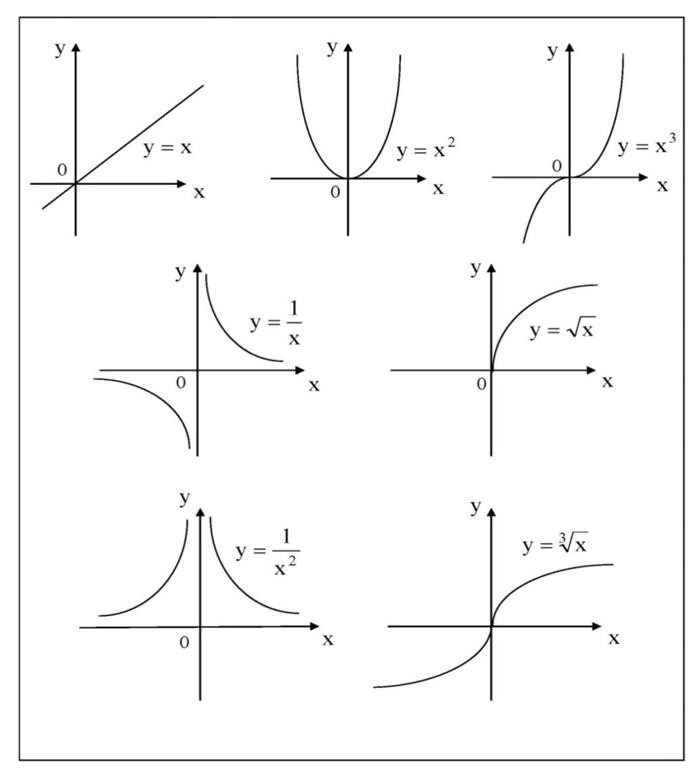
- Находим производные функции f'(x) и f”(x);
- Находим корни производных и точки, в которых производные не существуют;
- Анализируем знаки производных в найденных точках;
- Определяем экстремумы функции и их типы (максимум или минимум).
4. Исследование на выпуклость и точки перегиба:
- Находим вторую производную f”(x);
- Исследуем знаки второй производной, чтобы определить выпуклость и вогнутость функции;
- Находим корни второй производной, чтобы определить точки перегиба функции.
5. Задание таблицы значений и построение графика функции:
| x | f(x) |
|---|---|
| a | f(a) |
| между a и b | f(x) |
| b | f(b) |
По полученным данным составляем таблицу значений функции f(x) и строим график на координатной плоскости.
Исследование и построение функции позволяет более подробно изучить ее свойства, определить экстремумы, точки перегиба и установить, как ведет себя функция на заданном отрезке.
Корень n-й степени: определение, свойства и примеры
Корень n-й степени обозначается символом √ и индексом n, который указывает на степень, из которой извлекается корень. Например, √4 означает корень квадратный из числа 4, √27 – корень кубический из числа 27.
Свойства корня n-й степени:
- Если n – четное число, то корень n-й степени из отрицательного числа существует, и он также будет отрицательным числом. Например, √(-4) = -2.
- Если n – нечетное число, то корень n-й степени из отрицательного числа существует, и он будет комплексным числом. Например, √(-8) = 2i, где i – мнимая единица.
- Корень n-й степени из нуля равен нулю. Например, √0 = 0.
- Корень n-й степени из единицы равен единице. Например, √1 = 1.
- Корень n-й степени из положительного числа всегда положителен.
Примеры корня n-й степени:
| Число (x) | Степень (n) | Корень n-й степени (√x) |
|---|---|---|
| 4 | 2 | 2 |
| 27 | 3 | 3 |
| 81 | 4 | 3 |
| 0 | 5 | 0 |
Корень n-й степени имеет широкое применение в различных областях математики, физики и инженерии. Он используется, например, для решения уравнений, вычисления площадей, нахождения длин и объемов.
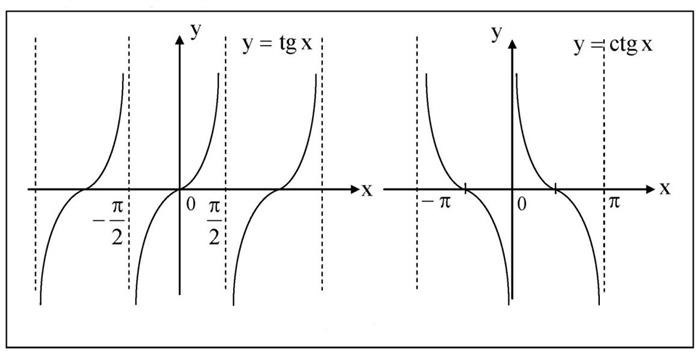
Правила построения графиков
1. Выбор масштаба осей
Перед началом построения графика необходимо выбрать масштаб осей. Масштаб должен быть выбран таким образом, чтобы данные были наглядны и график был четко видим. При выборе масштаба необходимо учесть диапазон значений переменных и выбрать наиболее подходящий интервал для осей.
2. Подпись осей и линий
Для удобства и понимания графика необходимо подписать оси и линии на графике. На оси абсцисс принято откладывать независимую переменную, а на оси ординат – зависимую переменную. Кроме того, необходимо подписать значения на каждой оси и обозначить единицы измерения.
3. Отметки на осях
Для более точного представления данных на графике необходимо использовать отметки на осях. Отметки на осях помогают определить значения на графике и легче считать координаты точек. Отметки на осях должны быть равномерно распределены и позволять четко определить значения данных.
4. Выделение ключевых точек
Для более точного анализа графика и выявления ключевых моментов необходимо выделить на графике ключевые точки. Ключевые точки могут быть экстремумами (максимумами и минимумами) или точками перегиба. Выделение ключевых точек позволяет лучше понять характер и свойства функции.
5. Использование цветов и стилей линий
При построении графиков можно использовать различные цвета и стили линий, чтобы лучше выделить различные элементы на графике. Например, можно использовать разные цвета линий для разных функций или разные стили линий для различных типов данных. Это помогает наглядно представить информацию и делает график более понятным.
Лекция 3. Предел последовательности. Числовые последовательности. Предел числовой последовательности.
Мы изучили основные свойства пределов последовательностей, такие как единственность предела, арифметические операции с пределами, связь между ограниченностью последовательности и ее пределом. Также мы рассмотрели несколько примеров расчета пределов числовых последовательностей.
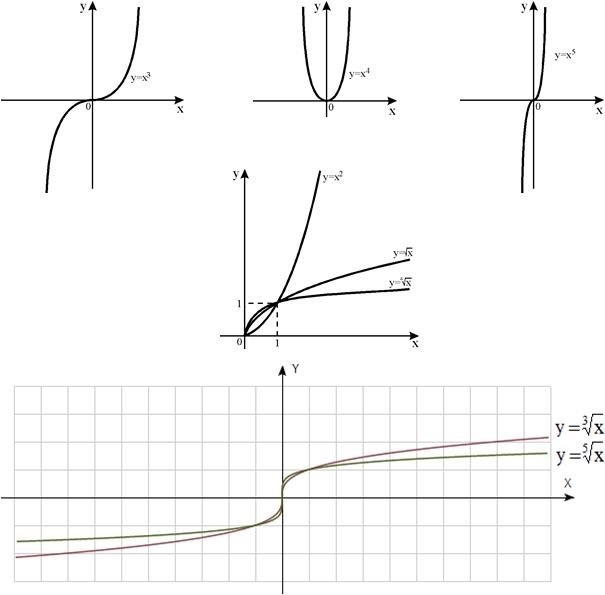
Числовая последовательность может иметь различные виды пределов: пределом может быть конкретное число, плюс или минус бесконечность, а также предел может не существовать.
Важно отметить, что понимание понятия предела последовательности является важным для дальнейшего изучения математического анализа и его применения в различных областях.