Если дан отрезок на плоскости с координатами концов (x1, y1) и (x2, y2), то координаты его середины будут равны:
x = (x1 + x2) / 2
y = (y1 + y2) / 2
Примеры применения формулы
Формула для вычисления середины отрезка на плоскости имеет широкое применение в различных областях математики, физики и инженерии. Эта формула позволяет определить точку на отрезке, которая расположена ровно посередине между двумя заданными точками.

1. Геометрия
В геометрии формула для определения середины отрезка используется для нахождения координат точки, которая делит отрезок на две равные части. Это может быть полезно при работе с фигурами и конструкциями, когда необходимо найти точку, которая находится посередине отрезка.
2. Картография
В картографии формула для вычисления середины отрезка может применяться для определения координат центра массы между двумя географическими точками. Например, при построении карт, где необходимо найти центр между двумя городами или точками маршрута.
3. Робототехника
В робототехнике формула для определения середины отрезка может использоваться для вычисления координат центра движения робота между двумя заданными точками. Это позволяет роботу точно определить свое положение и добраться до необходимой точки в кратчайшие сроки.
4. Конструкционное проектирование
В конструкционном проектировании формула для определения середины отрезка может быть применена для расчета точек стыковки между деталями конструкции. Это позволяет создавать прочные и устойчивые конструкции, обеспечивая равномерное распределение нагрузок.
Формула нахождения координаты середины отрезка
Отрезок в геометрии представляет собой часть прямой между двумя точками. Иногда возникает необходимость найти координаты середины этого отрезка. Для этого существует специальная формула, позволяющая с легкостью определить координаты середины отрезка. Формула основана на средних значениях координат начальной и конечной точек отрезка.
Общая формула
Пусть начальная точка отрезка имеет координаты (x1, y1), а конечная точка – (x2, y2). Тогда координаты середины отрезка равны:
x = (x1 + x2) / 2
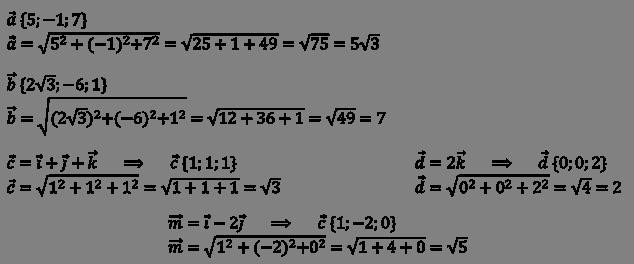
y = (y1 + y2) / 2
Примеры
Представим, что у нас есть отрезок, начальная точка которого имеет координаты (3, 5), а конечная точка – (9, 12). С помощью формулы можно легко найти координаты середины этого отрезка:
- Для нахождения координаты x: (3 + 9) / 2 = 6
- Для нахождения координаты y: (5 + 12) / 2 = 8.5
Таким образом, координаты середины отрезка с начальной точкой (3, 5) и конечной точкой (9, 12) равны (6, 8.5).
Значение формулы
Формула нахождения координаты середины отрезка помогает упростить и ускорить процесс вычисления этой величины. Она основана на принципе среднего и позволяет найти среднее значение между двумя точками, что является геометрическим аналогом арифметического среднего. Это полезно при решении задач, связанных с геометрией и расположением точек на плоскости.
Свойства середины отрезка
1. Координаты середины отрезка
Одно из основных свойств середины отрезка – равенство координат этой точки по отношению к концам отрезка. Если дан отрезок с координатами концов (x₁, y₁) и (x₂, y₂), то координаты середины (x, y) можно вычислить следующим образом:
x = (x₁ + x₂) / 2
y = (y₁ + y₂) / 2

2. Центр симметрии
Середина отрезка является центром симметрии для данного отрезка. Это означает, что отрезок можно “сложить” по середине, совместив две его половины, при этом они будут абсолютно одинаковыми. Таким образом, середина отрезка делит его на две симметричные части.
3. Расстояние от начала отрезка до его середины
Расстояние от начала отрезка до его середины равно половине длины этого отрезка. Это свойство может использоваться для вычисления расстояния между точками или для нахождения других характеристик отрезков.
4. Коллинеарные точки
Точки, лежащие на одном отрезке, являются коллинеарными точками. Середина отрезка также является коллинеарной точкой, что означает, что она лежит на этом отрезке.
5. Значение середины отрезка в геометрических построениях
Середина отрезка имеет важное значение в геометрических построениях, таких как построение треугольника по двум сторонам или нахождение центра тяжести фигуры. Знание координат середины отрезка может облегчить и ускорить процесс этих возможных задач.
Формулы вычисления расстояния между двумя точками:
Расстояние между двумя точками в пространстве можно вычислить с помощью формулы, исходя из координат этих точек. Существует две основные формулы для вычисления расстояния: формула декартовой системы координат и формула с использованием координатных плоскостей.
1. Формула декартовой системы координат:
Для двух точек с координатами (x₁, y₁, z₁) и (x₂, y₂, z₂) в пространстве формула для вычисления расстояния выглядит следующим образом:
d = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²)
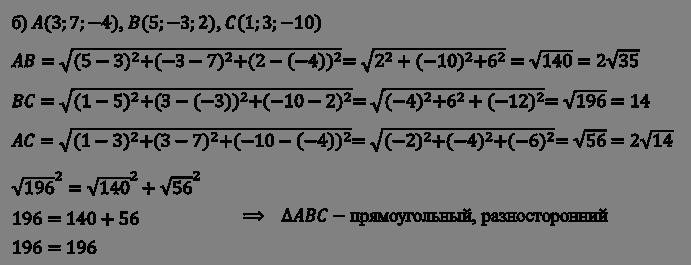
В этой формуле каждая координата середины отрезка вычисляется как среднее арифметическое между соответствующими координатами концов отрезка.
2. Формула с использованием координатных плоскостей:
Для двух точек с координатами (x₁, y₁) и (x₂, y₂) в плоскости формула для вычисления расстояния имеет следующий вид:
d = √((x₂ – x₁)² + (y₂ – y₁)²)
Используя эти формулы, можно вычислить расстояние между двумя точками в пространстве или на плоскости.
Итог:
Вычисление расстояния между двумя точками в пространстве или на плоскости является важной задачей в геометрии. Существуют две основные формулы для расчета расстояния: формула декартовой системы координат и формула с использованием координатных плоскостей. Обе формулы основаны на вычислении разницы между соответствующими координатами двух точек и на применении пифагоровой теоремы для расчета расстояния от начальной точки до конечной точки. Использование этих формул поможет вам определить расстояние между любыми двумя точками в пространстве или на плоскости.