Граф – это абстрактная структура данных, которая представляет собой набор вершин и ребер, связывающих эти вершины. Графы широко используются в информатике для моделирования и решения различных задач, таких как поиск пути, анализ связей и организация данных.
Кратные рёбра и петли
Кратные рёбра
Кратные рёбра – это рёбра, которые соединяют одну и ту же пару вершин. Они могут иметь разные веса или свойства, но их начало и конец совпадают. Наличие кратных рёбер может повлиять на алгоритмы работы с графами, такие как поиск кратчайшего пути или проверка связности.
Примеры использования кратных рёбер:
- Множественные дороги между двумя городами.
- Переходы между различными состояниями автомата.
- Множественные связи в социальных сетях.
Петли
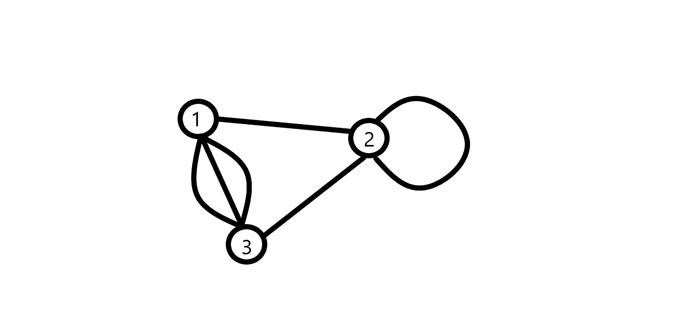
Петли – это ребра, которые соединяют вершину с самой собой. Они могут быть полезными в некоторых задачах, но также могут вызвать проблемы при выполнении некоторых алгоритмов.
Примеры использования петель:
- Состояния автомата, которые могут быть достигнуты из себя же.
- Циклы в генетических алгоритмах.
- Обратная связь в нейронных сетях.
Влияние на алгоритмы
Кратные рёбра и петли могут влиять на результат работы различных алгоритмов обработки графов. В некоторых случаях они могут привести к неправильным или бесконечным результатам.
Некоторые алгоритмы и их реакция на кратные рёбра и петли:
| Алгоритм | Реакция на кратные рёбра | Реакция на петли |
|---|---|---|
| Поиск кратчайшего пути | Могут появиться альтернативные пути | Могут возникнуть бесконечные циклы |
| Поиск связности | Может быть неоднозначная связность | Могут возникнуть циклические компоненты |
| Топологическая сортировка | Могут возникнуть проблемы с определением порядка | Могут возникнуть проблемы с определением порядка |
Исходя из вышесказанного, при анализе и обработке графов необходимо учитывать наличие кратных рёбер и петель и применять специальные стратегии и алгоритмы для их обработки.
Что такое граф
Графы широко используются в информатике, чтобы представлять различные типы данных и связи между ними. Они находят применение в задачах маршрутизации, социальных сетях, графических алгоритмах, анализе данных и многих других областях.
Классификация графов
Графы можно классифицировать по различным критериям. Вот несколько основных классификаций:
- Направленность: граф может быть направленным (ориентированным) или ненаправленным (неориентированным). В направленном графе ребра имеют определенное направление, в то время как в ненаправленном графе ребра не имеют направления.
- Взвешенность: граф может быть взвешенным или невзвешенным. Взвешенный граф имеет значения или веса на ребрах, которые указывают на стоимость или расстояние между вершинами.
- Специальные свойства: графы могут иметь различные специальные свойства, такие как связность (все вершины связаны друг с другом), деревья (граф без циклов), двудольность (вершины разделены на две группы, где ребра соединяют только вершины из разных групп) и т. д.
Реализация на C++
Реализация графов на C++ может основываться на различных структурах данных. Несколько популярных способов включают использование матрицы смежности и списка смежности.
Матрица смежности: Матрица смежности представляет граф в виде двумерного массива, где элемент [i][j] указывает наличие ребра между вершинами i и j. Значение элемента может быть весом ребра или логическим флагом. Этот метод хорошо подходит для небольших графов, но может потребовать много памяти для больших или разреженных графов.
Список смежности: Список смежности представляет граф в виде списка, где каждая вершина имеет список своих соседей. Этот метод более эффективен для больших или разреженных графов, так как требует меньше памяти. Он также облегчает операции, такие как обходы графа.
| Вершина | Список соседей |
|---|---|
| 0 | [1, 2, 3] |
| 1 | [0, 2] |
| 2 | [0, 1, 3] |
| 3 | [0, 2] |
В этой таблице каждая вершина представлена числом, а список соседей указывает на другие вершины, с которыми данная вершина связана.
Создание графа и методы его представления
В информатике граф представляет собой математическую абстракцию, которая используется для моделирования различных ситуаций. Создание графа состоит из нескольких шагов, включая определение вершин и рёбер, а также выбор метода представления.
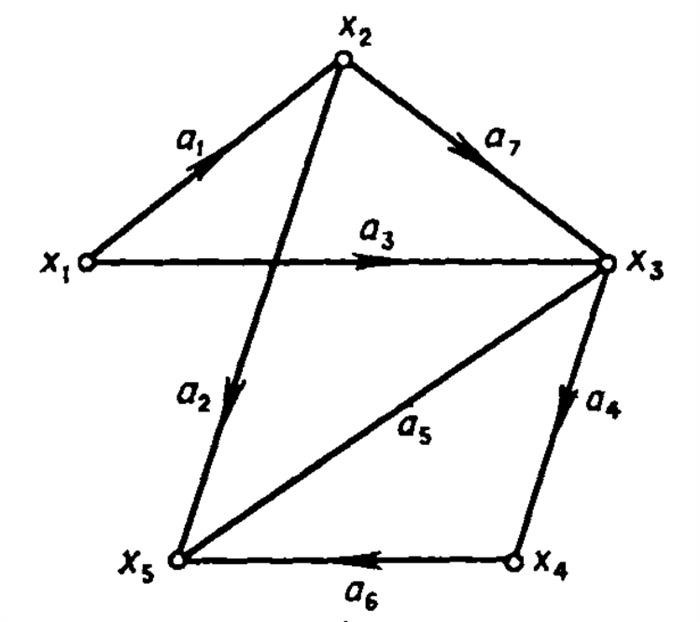
Определение вершин и рёбер
Первый шаг при создании графа – определение его вершин. Вершины могут представлять отдельные объекты, события или действия. Далее необходимо определить рёбра, которые соединяют вершины. Рёбра могут иметь различные характеристики, например, вес или направление.
Методы представления графа
Существует несколько методов представления графа, каждый из которых имеет свои преимущества и ограничения. Некоторые из наиболее распространенных методов включают:
-
Матрица смежности: граф представляется в виде квадратной матрицы, где каждая ячейка указывает наличие ребра между вершинами. Этот метод эффективен для поиска связей между вершинами, но требует большего объема памяти для хранения информации о графе.
-
Список смежности: граф представляется в виде списка, где каждая вершина имеет список смежных с ней вершин. Этот метод более экономичен по памяти, но может быть менее эффективным для поиска связей в графе.
-
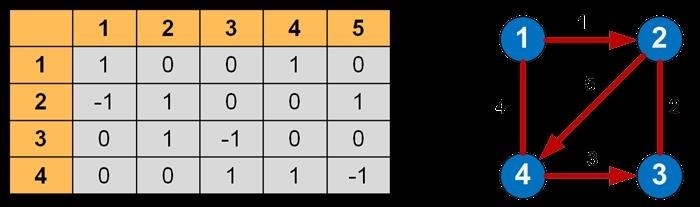
Матрица инцидентности: граф представляется в виде матрицы, где каждая строка представляет вершину, а каждый столбец – ребро. Каждая ячейка матрицы указывает наличие ребра между вершиной и ребром. Этот метод удобен для работы с ориентированными графами и позволяет эффективно определять смежные вершины и ребра.
Создание графа в информатике включает определение вершин и рёбер, а также выбор метода их представления. Методы представления графа включают матрицу смежности, список смежности и матрицу инцидентности. Каждый из этих методов имеет свои преимущества и предназначен для определенного набора задач.
Алгоритмы обхода графов
Типы алгоритмов обхода графов
- Алгоритмы обхода в ширину – рассматривают все вершины на одной глубине от начальной вершины перед переходом к вершинам следующей глубины.
- Алгоритмы обхода в глубину – исследуют каждую вершину до ее полного исследования, прежде чем переходить к следующей вершине.
- Алгоритмы обхода поиска в ширину с ограничением глубины – ограничивают глубину обхода и прекращают исследование подграфа на определенном уровне глубины.
- Алгоритмы обхода поиска в глубину с ограничением ширины – ограничивают ширину обхода и прекращают исследование подграфа после определенного числа просмотренных вершин.
В зависимости от задачи и структуры графа выбираются соответствующие алгоритмы обхода, чтобы оптимально найти и исследовать все вершины графа. Алгоритмы обхода графов являются важным инструментом для решения многих информационных задач.
Пример: обход графа в ширину
Один из примеров алгоритма обхода графа в ширину – алгоритм поиска в ширину (BFS). Он начинает с указанной вершины и постепенно просматривает все ближайшие вершины, прежде чем переходить к следующим ближайшим вершинам.
Алгоритм BFS можно представить в виде следующих шагов:
- Поместить начальную вершину в очередь.
- Пока очередь не пуста, извлечь вершину из очереди и просмотреть ее.
- Добавить все непосещенные соседние вершины в очередь и пометить их как посещенные.
- Повторять шаги 2 и 3, пока все вершины не будут просмотрены.
Алгоритм обхода графа в ширину позволяет найти кратчайший путь от начальной вершины ко всем остальным вершинам графа. Он является одним из основных алгоритмов для решения различных информационных задач, связанных с обходом графов.
Основные понятия теории графов
Основные понятия теории графов включают в себя:
1. Вершины (узлы)
Вершина – это основной элемент графа, представленный точкой или кружком. Каждая вершина имеет уникальное имя или метку для идентификации. Вершины могут быть связаны ребрами, которые отображают взаимодействие или соединение между двумя вершинами.
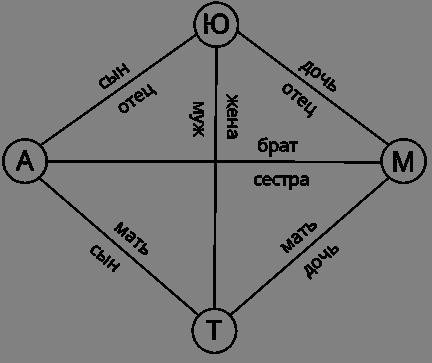
2. Ребра (дуги)
Ребро – это связь между двумя вершинами графа. Оно может быть представлено линией или стрелкой, указывающей направление. Ребра могут быть направленными или ненаправленными, в зависимости от того, существуют ли ограничения на направление движения между вершинами.
3. Ориентированные и неориентированные графы
Ориентированный граф – это граф, в котором ребра имеют направление. Направление определяется стрелкой, указывающей на порядок перехода от одной вершины к другой. Неориентированный граф – это граф, в котором ребра не имеют направления и могут быть пройдены в обоих направлениях.
4. Соседство и степень вершин
Соседство – это связь между двумя вершинами графа, когда они соединены ребром. Если две вершины связаны ребром, то они считаются соседними. Степень вершины – это количество ребер, исходящих или входящих в данную вершину. Степень вершины может быть равна нулю, если вершина не имеет соседей.
5. Пути и циклы
Путь представляет собой последовательность вершин, соединенных ребрами. Путь может быть прямым или вынужденным. Прямой путь проходит через различные вершины и ребра графа без повторений. Вынужденный путь может содержать повторяющиеся вершины и ребра. Цикл – это путь, в котором начальная и конечная вершины совпадают.
6. Связность графа
Связность графа – это свойство графа, указывающее, насколько тесно связаны его вершины. Граф может быть связанным или несвязанным. Связный граф – это граф, в котором существует путь между любыми двумя вершинами. Несвязный граф состоит из двух или более отдельных компонентов, которые не связаны между собой.
7. Взвешенные графы
Взвешенный граф – это граф, в котором каждому ребру присвоено числовое значение или вес. Вес может представлять различные характеристики, такие как стоимость, расстояние или время. Взвешенные графы используются для моделирования и решения различных задач, таких как кратчайший путь или минимальное остовное дерево.
Теория графов предоставляет широкий спектр инструментов и методов для анализа, моделирования и решения различных задач и проблем. Эти основные понятия являются фундаментальными для дальнейшего изучения этого интересного математического раздела.
Пути и циклы в графах: основные понятия и примеры
Пути в графах
Путь в графе – это последовательность вершин, которые соединены ребрами друг с другом. Каждое ребро в пути обязательно должно иметь общую вершину с предыдущим и следующим ребром. Путь может быть направленным или ненаправленным, в зависимости от того, разрешено ли движение только в определенном направлении.
Существуют различные типы путей в графах:
- Простой путь – это путь, в котором все вершины уникальны, то есть каждая вершина встречается только один раз.
- Цикл – это путь, в котором первая и последняя вершины совпадают. Таким образом, цикл образует замкнутую последовательность вершин.
- Простой цикл – это цикл, в котором все вершины, кроме первой и последней, уникальны.
Пути играют важную роль при анализе графов. Например, нахождение кратчайшего пути между двумя вершинами – это одна из классических задач, которые решаются с использованием графов.
Примеры путей в графах
Рассмотрим пример графа, в котором изображены различные пути:
| Вершина | Путь |
|---|---|
| A | A – B – C – D – E |
| B | B – C – D – E |
| C | C – D – E |
| D | D – E |
В данном примере показаны различные пути от вершины А до вершины Е. Каждый путь представляет собой последовательность вершин, соединенных ребрами между собой. Данный граф является направленным, то есть путь можно пройти только в одном направлении.
Циклы в графах
Цикл в графе – это замкнутый путь, в котором первая и последняя вершины совпадают. Цикл может быть простым или состоять из повторяющихся вершин. Циклы в графах могут иметь различную длину и сложность.
Примеры различных циклов в графах:
- Простой цикл: A – B – C – D – E – A
- Цикл из повторяющихся вершин: A – B – C – B – A
- Цикл длины 1: A – A
Циклы играют важную роль при анализе графов, так как позволяют определить замкнутые пути и выявить особенности структуры графа.
Ориентированные и неориентированные графы
Графами называются структуры данных, которые используются в информатике для представления и анализа связей между объектами. В графах выделяют два основных типа: ориентированные и неориентированные.
Ориентированные графы
Ориентированный граф представляет собой совокупность вершин и дуг, где каждая дуга имеет направление. В ориентированных графах можно проследить направление связей между вершинами. Такой тип графа широко используется для моделирования различных процессов, например, в компьютерных сетях или планировании маршрутов.
- Каждая дуга в ориентированном графе имеет начальную и конечную вершину.
- Между двумя вершинами может быть несколько дуг с разными направлениями.
- Ориентированный граф часто используется для моделирования зависимостей и последовательностей.
Неориентированные графы
Неориентированный граф представляет собой совокупность вершин и ребер, где ребра не имеют направления. Этот тип графа используется, когда связи между объектами являются симметричными и не имеют определенного направления. Неориентированные графы широко применяются в анализе социальных сетей, моделировании дружеских связей и транспортных сетей.
- Ребра в неориентированном графе не имеют начала и конца.
- Связи между вершинами являются взаимными и не имеют определенного направления.
- Неориентированный граф позволяет исследовать связи между объектами без учета направления.
Ориентированные и неориентированные графы имеют свои особенности и применяются в различных областях. Выбор между ними зависит от контекста задачи и требований к представлению связей между объектами.
Циклы в графе
Однако в графе могут также существовать и другие типы циклов, например, петли и компоненты сильной связности. Петля – это цикл, состоящий из одного ребра, соединяющего вершину с самой собой. Компонента сильной связности представляет собой подграф графа, в котором каждая вершина достижима из всех других вершин данной компоненты.