Угол между векторами определяется с помощью скалярного произведения векторов. Скалярное произведение векторов является числовой величиной, равной произведению модулей векторов и косинуса угла между ними. Формула для нахождения угла между векторами дает возможность определить величину и направление угла. Угол между векторами может быть острый, прямой или тупой, в зависимости от знака скалярного произведения. Кроме того, угол между векторами можно выразить в радианах или градусах.
Примеры вычислений скалярного произведения
Пример 1: Вычисление длины вектора
Для вычисления длины вектора можно воспользоваться скалярным произведением и следующей формулой:
||a|| = √(a · a)
где ||a|| – длина вектора a.

Пример 2: Вычисление угла между двумя векторами
Угол между двумя ненулевыми векторами можно вычислить с помощью скалярного произведения и следующей формулы:
cos(θ) = (a · b) / (||a|| ||b||)
где θ – угол между векторами a и b.
Пример 3: Проверка ортогональности векторов
Для проверки ортогональности двух векторов необходимо вычислить их скалярное произведение. Если скалярное произведение равно нулю, то векторы являются ортогональными.
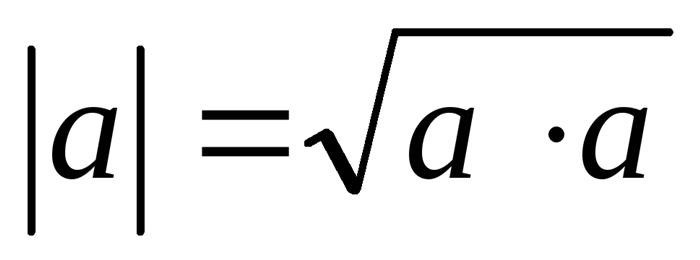
Пример:
| a | b | a · b |
|---|---|---|
| [2, 3] | [4, -2] | 2*4 + 3*(-2) = 8 – 6 = 2 |
Скалярное произведение векторов a и b равно 2, что не равно нулю. Значит, эти векторы не являются ортогональными.
Пример 4: Вычисление работы силы
Для вычисления работы силы по формуле F · s, где F – сила, s – смещение, необходимо использовать скалярное произведение векторов F и s.
Пример:
| F | s | F · s |
|---|---|---|
| [3, 2] | [4, 5] | 3*4 + 2*5 = 12 + 10 = 22 |
Работа силы, приложенной к объекту со смещением s, равна 22.
Таким образом, скалярное произведение векторов позволяет решать различные задачи, такие как вычисление длины вектора, определение угла между векторами, проверка ортогональности и вычисление работы силы.
Векторное произведение двух векторов, его свойства
Свойства векторного произведения:
- Направление: Векторное произведение двух векторов перпендикулярно плоскости, образуемой исходными векторами. Направление вектора определяется правилом буравчика, которое указывает, что векторное произведение считается положительным, если поворот от первого вектора ко второму осуществляется против часовой стрелки, и отрицательным в противоположном случае.
- Длина: Длина векторного произведения двух векторов равна площади параллелограмма, образованного исходными векторами. Длина произведения также равна произведению длин синуса угла между векторами на длину исходных векторов.
- Коммутативность: Векторное произведение обладает свойством антикоммутативности. Это означает, что порядок векторов важен, и в общем случае, векторное произведение вектора A на вектор B не равно векторному произведению вектора B на вектор A.
- Линейность: Векторное произведение подчиняется линейному закону. Это означает, что векторное произведение суммы векторов равно сумме векторных произведений этих векторов.
Таблица свойств векторного произведения:
| Свойство | Формула | Примечание |
|---|---|---|
| Направление | ( vec{A} times vec{B} = -vec{B} times vec{A} ) | – |
| Длина | ( |vecA} times vec|sintheta ) | ( theta ) – угол между векторами |
| Коммутативность | ( vec{A} times vec{B}eq vec{B} times vec{A} ) | – |
| Линейность | ( vec{A} times (vec{B} + vec{C}) = vec{A} times vec{B} + vec{A} times vec{C} ) | – |
Векторное произведение двух векторов позволяет не только определить перпендикулярный вектор, но и вычислить площадь параллелограмма, который образуют эти векторы. Кроме того, оно находит применение в задачах, связанных с моментом силы, магнитным полем и другими физическими явлениями.
Итог
В данной статье мы рассмотрели угол между векторами и способы его нахождения с использованием скалярного произведения векторов. Угол между двумя векторами определяется как угол между направлениями этих векторов.

Мы исследовали различные методы нахождения угла между векторами, включая использование геометрических свойств, тригонометрических функций и скалярного произведения векторов. В частности, скалярное произведение векторов позволяет найти косинус угла между векторами, а затем получить сам угол с помощью обратных тригонометрических функций.
Изучение угла между векторами имеет множество практических применений. Например, в физике и инженерии он используется для определения направления и силы векторных величин, а в компьютерной графике – для задания поворотов и трансформаций объектов.
Важно помнить, что угол между векторами может быть как острый, так и тупой, и может быть выражен в радианах или градусах. Также стоит отметить, что скалярное произведение векторов может быть использовано для определения ортогональности векторов и расчета длины вектора.