Угловой коэффициент касательной к графику функции

Угловой коэффициент касательной к графику функции является важным понятием в математике и представляет собой значение, показывающее, как меняется наклон касательной к графику функции в заданной точке. Этот коэффициент позволяет определить, какое угловое отношение существует между осью абсцисс и касательной, а также применяется для решения различных задач, связанных с изучением и анализом функций.

Основные значения угла наклона прямой

1. Прямая, параллельная оси абсцисс

Если угловой коэффициент равен нулю, то это означает, что график функции является прямой, параллельной оси абсцисс. В данном случае, прямая не имеет наклона и проходит горизонтально.

2. Прямая, параллельная оси ординат

Если угловой коэффициент не определен, то это означает, что график функции является вертикальной прямой, параллельной оси ординат. В данном случае, прямая не имеет уклона и проходит вертикально.

3. Положительное значение углового коэффициента

Если угловой коэффициент положителен, то это означает, что график функции стремится к верхнему направлению. Чем больше значение углового коэффициента, тем круче будет наклон прямой.

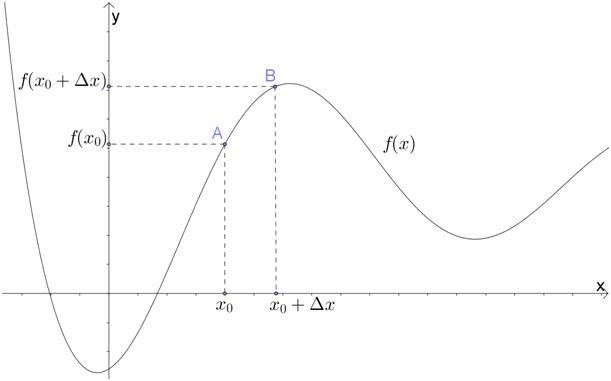
4. Отрицательное значение углового коэффициента

Если угловой коэффициент отрицателен, то это означает, что график функции стремится к нижнему направлению. Чем меньше значение углового коэффициента (или чем больше его модуль), тем круче будет наклон прямой.

Значение производной функции в точке и ее геометрический смысл

Геометрическое определение производной

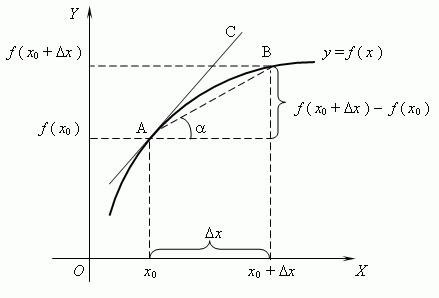
Геометрический смысл производной функции в точке заключается в том, что она определяет тангенс угла наклона касательной к графику функции в этой точке. Если значение производной положительно, то касательная наклонена вправо, если отрицательно – влево. Чем больше по модулю значение производной, тем круче наклон касательной.

Таблица значений производной

Точка	Значение производной	Наклон
x = a	f'(a)	Вертикальная касательная
x > a	f'(a) > 0	Наклон вправо
x < a	f'(a) < 0	Наклон влево

Примеры графиков функций

• Если значение производной функции равно 0 в точке, то касательная к графику функции горизонтальна.
• Если значение производной функции положительно в точке, то касательная к графику функции наклонена к правому углу.
• Если значение производной функции отрицательно в точке, то касательная к графику функции наклонена к левому углу.

Значение производной функции в точке имеет большое значение при решении задач оптимизации, поиске экстремумов функции и анализе поведения функции в окрестности заданной точки. Она позволяет определить, как функция будет вести себя вблизи данной точки и какие экстремумы она может иметь.

Понятие уравнения касательной прямой

Уравнение касательной прямой задается в виде y = kx + b, где k – угловой коэффициент, а b – точка пересечения с осью ординат. Угловой коэффициент k определяет наклон касательной прямой к оси абсцисс и является тангенсом угла наклона. Точка пересечения с осью ординат b указывает на значение функции y при x = 0.

Уравнение касательной прямой в различных случаях

• Если касательная прямая параллельна оси ординат, то ее уравнение имеет вид x = a, где a – значение координаты точки, через которую проходит касательная.
• Если касательная прямая параллельна оси абсцисс, то ее уравнение имеет вид y = b, где b – значение координаты точки, через которую проходит касательная.
• Если касательная прямая вертикальна, то уравнение ее нельзя описать в виде y = kx + b, так как угловой коэффициент не определен. В этом случае уравнение записывается в виде x = c, где c – значение координаты точки, через которую проходит касательная.

Пример решения задачи на поиск уравнения касательной прямой

Исходные данные:	Функция: y = 2x 2 + 3x – 1	Точка касания: (1, 4)
Найдем угловой коэффициент:	k = f'(x)	k = 4x + 3
Подставим x = 1:	k = 4 + 3	k = 7
Найдем b:	b = y – kx	b = 4 – 7 * 1	b = -3
Уравнение касательной прямой:	y = 7x – 3

Таким образом, уравнение касательной прямой к графику функции y = 2x 2 + 3x – 1 в точке (1, 4) будет иметь вид y = 7x – 3.

Как подготовиться к экзамену?

1. Создайте расписание

Планирование времени – важный аспект подготовки к экзамену. Создайте расписание, где вы разделите время на изучение различных предметов. Установите приоритеты и уделите больше времени на более сложные темы или предметы.

2. Сделайте обзор материала

Прежде чем начать детальное изучение каждой темы, сделайте обзор материала. Прочитайте учебник или лекционные записи, чтобы получить общее представление о теме. Выделите ключевые понятия и основные идеи.

3. Изучайте поэтапно

Разделите материал на более мелкие части и изучайте их поэтапно. Уделите достаточно времени на каждую часть, чтобы полностью понять ее. Используйте различные методы изучения, такие как чтение, запись, объяснение материала другим, чтобы лучше запомнить его.

4. Практикуйтесь с помощью задач и тестов

Практика помогает вам проверить свои знания и подготовиться к типичным вопросам, которые могут встретиться на экзамене. Решайте задачи и выполняйте тесты, чтобы улучшить свои навыки и привыкнуть к формату экзамена.

5. Работайте в группе

Обсуждение материала с другими студентами может помочь вам лучше его понять и запомнить. Работа в группе позволяет обмениваться идеями, задавать вопросы и объяснять материал друг другу.

6. Отдыхайте и заботьтесь о своем здоровье

Не забывайте об отдыхе и заботе о своем здоровье. Недостаток сна и плохое питание могут отрицательно повлиять на вашу способность усваивать информацию и концентрироваться. Уделите время для активности, отдыха и здорового питания.

7. Задавайте вопросы преподавателю

Если у вас возникли вопросы или затруднения, не стесняйтесь спрашивать преподавателя. Они могут дать вам дополнительные объяснения и помочь разобраться с темой.

8. Повторяйте и повторяйте

Повторение – ключевой фактор запоминания материала. Периодически повторяйте изученный материал, чтобы закрепить его в памяти. Создайте карточки с определениями и ключевыми понятиями, которые вы можете использовать для повторения.

9. Подготовьтесь к формату экзамена

Изучите требования и формат экзамена заранее. Узнайте, какие типы вопросов будут заданы и какой будет продолжительность экзамена. Практикуйтесь, используя примеры экзаменационных вопросов, чтобы быть готовыми к самому экзамену.

10. Оставьте время для последнего повторения

Не оставляйте повторение на последний момент. Оставьте достаточно времени для последнего повторения материала перед экзаменом. Это поможет вам освежить свою память и повысить уверенность в своих знаниях.

Следуя этим советам, вы сможете хорошо подготовиться к экзамену и повысить свои шансы на успех.

§ 6.2. Вычисление производных

Понятие производной

Производная функции в точке определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Производная показывает наклон касательной к графику функции в данной точке.

Способы вычисления производной

Существует несколько способов вычисления производных. Вот некоторые из них:

1. По определению. Если функция задана явно, то производную можно вычислить по формуле, используя предел.
2. По правилам дифференцирования. Существуют некоторые простые правила, которые позволяют найти производные для разных видов функций, например, линейных, степенных, экспоненциальных, логарифмических и т.д.
3. С помощью таблицы производных. Существует таблица, которая содержит производные для разных функций. Используя эту таблицу, можно найти производную без необходимости вычислять ее по определению или правилам.

Производные как инструмент решения задач

Производные находят широкое применение в различных областях науки и техники. Вот некоторые из них:

• Оптимизация. Производная позволяет найти экстремумы функций, что полезно при поиске максимумов и минимумов.
• Анализ графиков. Производная позволяет определить направление изменения функции в каждой точке, наличие экстремумов и точек перегиба.
• Физика. Производная используется для расчета скорости, ускорения, измерения изменения величин в разных физических явлениях.
• Финансы. Производная используется для анализа финансовых показателей, оценки рисков и т.д.

Вычисление производных играет важную роль в математике и ее применении в других областях. Знание производных и умение их находить помогает понять и анализировать поведение функций и применять математические методы к различным задачам.

Уравнение касательной к графику функции – коротко о главном

Уравнение касательной

Уравнение касательной к графику функции в заданной точке выглядит следующим образом:

y – y₀ = k(x – x₀)

Где:

• y – значение функции в точке на касательной
• x – координата данной точки
• y₀ – значение функции в заданной точке
• x₀ – координата заданной точки
• k – угловой коэффициент касательной

Нахождение углового коэффициента

Угловой коэффициент касательной определяется как тангенс угла наклона касательной к оси абсцисс. Можно выразить его следующим образом:

k = f'(x₀)

Где:

• f'(x₀) – производная функции в точке

Зная значение производной функции в заданной точке, мы можем определить угловой коэффициент касательной и использовать его для построения уравнения касательной.

Пример

Рассмотрим пример функции f(x) = 2x² – 3x + 1. Найдем уравнение касательной к графику этой функции в точке с координатами (2, 3).

Сначала найдем производную функции: f'(x) = 4x – 3.

Затем найдем значение производной в заданной точке: f'(2) = 4 * 2 – 3 = 5.

Теперь, имея значение производной и заданные координаты точки, можем записать уравнение касательной:

y – 3 = 5(x – 2)

Это уравнение касательной позволит нам определить значение функции и приблизить график функции в окрестности точки (2, 3).

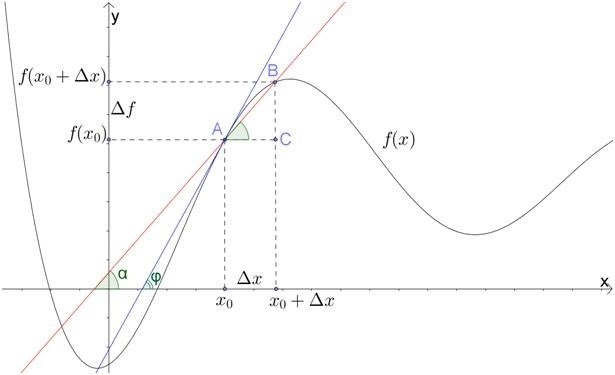
Геометрический смысл производной

Производная функции в математике имеет важное геометрическое значение. Она показывает наклон касательной к графику функции в каждой точке. Таким образом, производная позволяет определить угловой коэффициент касательной и понять, как функция меняется в данной точке.

Если производная положительна, то касательная к графику функции имеет положительный наклон (т.е. направлена вверх), что означает возрастание функции в данной точке. Если производная отрицательна, то касательная имеет отрицательный наклон (т.е. направлена вниз), что означает убывание функции.

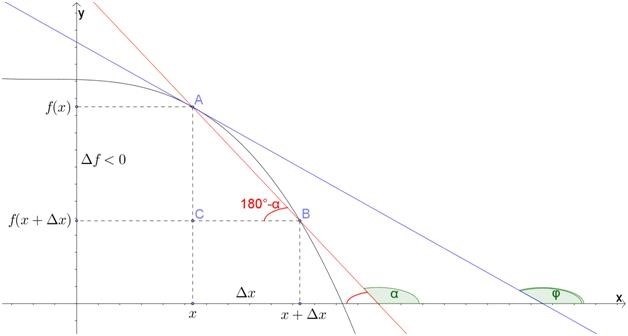
Если производная равна нулю, то график функции имеет горизонтальную касательную. Это означает, что функция имеет экстремум – минимум или максимум – в данной точке.

С помощью производной можно также определить точки перегиба на графике функции. В точке перегиба касательная графика меняет свое направление, что соответствует равенству нулю второй производной функции.

Итак, геометрический смысл производной заключается в определении наклона касательной и изменения функции в каждой точке. Производная позволяет анализировать график функции и находить такие характеристики, как возрастание, убывание, экстремумы и точки перегиба.