Логика – это наука о правильном мышлении и рассуждении. Она играет важную роль в наших повседневных решениях и анализе информации. В данной статье мы рассмотрим 4 основных закона логики – закон исключенного третьего, закон противоречия, закон двойного отрицания и закон идентичности. Каждый из этих законов будет пояснен примерами из реальной жизни и математики.
Закон тождества
Формулировка закона тождества:
“Каждое высказывание A равно самому себе: A = A”
Закон тождества можно рассматривать с различных точек зрения:
-
Математика: В математике закон тождества применяется для доказательства равенств и тождеств, а также для приведения выражений к более простому виду.

-
Философия: В философии закон тождества отражает принцип идентичности, где объект или концепция всегда равна самой себе и не может быть ничему другому.
-
Логика: В логике закон тождества используется для определения эквивалентности двух высказываний и их приведения к одинаковому виду.
Примеры применения закона тождества:

| Высказывание A | Равно A = A |
|---|---|
| 2 + 2 = 4 | 2 + 2 = 4 |
| “Солнце встает на востоке” | “Солнце встает на востоке” |
| 5 – 3 = 2 | 5 – 3 = 2 |
Закон тождества является фундаментальным принципом логики и имеет широкое применение в различных областях знания.
Закон достаточного основания (открыт римским врачом Галеном)
Суть закона достаточного основания
Примеры применения закона достаточного основания
- Пример 1: Если требуется доказать вину подозреваемого в убийстве, необходимо представить достаточное основание, такие как доказательства присутствия подозреваемого на месте преступления, свидетельские показания и т.д.
- Пример 2: В медицине, чтобы поставить точный диагноз и предписать соответствующее лечение, врач должен иметь достаточные основания в виде анализов, обследований и медицинских исследований.
Значение закона достаточного основания
Законы логики по Аристотелю
Закон тождества
Закон тождества утверждает, что если высказывание истинно, то оно и остается истинным в любых условиях. В юридическом контексте это означает, что если некоторый факт описан в документе или установлен в рамках законодательства, то он сохраняет свою силу и не может быть опровергнут в последующих судебных процессах.
Закон невозможности
Закон невозможности утверждает, что нельзя одновременно утверждать противоречивые высказывания. В контексте права это означает, что если есть две непримиримых стороны или интереса, то невозможно прийти к общему решению или соглашению, и дело может быть разрешено только судом или другим компетентным органом.

Закон исключённого третьего
Закон исключённого третьего утверждает, что между истиной и ложью нет третьего варианта. В сфере права это означает, что суд при рассмотрении дела должен принимать решение на основе имеющихся доказательств и законодательства, и не может сделать никакого иного выбора.
Закон недоказанности отрицательного
Закон недоказанности отрицательного утверждает, что отсутствие доказательств противоречащего факта не является доказательством самого факта. В контексте юридической практики это означает, что сторона, обвиняющая кого-либо в правонарушении или преступлении, должна представить достаточные доказательства, а не только отсутствие доказательств противоположного.
Итог
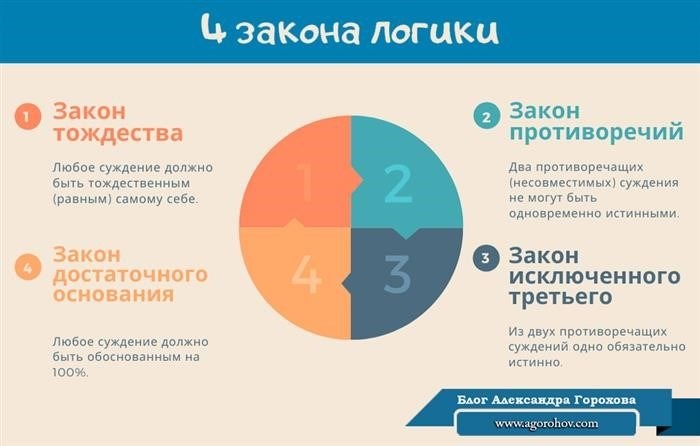
В данной статье мы рассмотрели и объяснили четыре основных закона логики: закон исключенного третьего, закон противоречия, закон двойного отрицания и закон идемпотентности.
Закон исключенного третьего утверждает, что любое утверждение либо истинно, либо ложно, без промежуточных значений. Примером этого закона может служить утверждение “Сегодня идет дождь, или нет”. Всего два возможных варианта ответа – либо дождь идет, либо нет, других вариантов быть не может.
Закон противоречия утверждает, что нельзя одновременно утверждать и отрицать одно и то же утверждение. Примером этого закона может служить утверждение “Это яблоко одновременно зеленое и не зеленое”. Из этого утверждения следует противоречие, так как яблоко не может быть и зеленым и не зеленым одновременно.
Закон двойного отрицания утверждает, что дважды отрицанное утверждение равносильно исходному утверждению. Например, утверждение “Ты не понимаешь ничего” эквивалентно утверждению “Ты понимаешь все”. Оба утверждения означают, что у тебя есть полное понимание или полное непонимание ситуации.
Закон идемпотентности утверждает, что дважды одно и то же утверждение равносильно исходному утверждению. Например, утверждение “Я тебе говорил, что сегодня будет дождь” эквивалентно утверждению “Я тебе говорил”. В обоих случаях выражается одно и то же.