Свойство вычитания числа из суммы – это свойство алгебры, которое гласит, что можно вычесть число из суммы, равносильно вычитанию этого числа из каждого слагаемого исходной суммы. Иными словами, можно вычесть число из всей суммы или из каждого слагаемого по отдельности, результат будет одинаковым.
Натуральные числа: сложение и вычитание
Сложение натуральных чисел
Сложение натуральных чисел – это операция, при которой два или более числа объединяются в одну сумму. Когда мы складываем натуральные числа, мы увеличиваем их значение.
Для сложения натуральных чисел используется знак “+”. Например, 3 + 2 = 5, где 3 и 2 – слагаемые, а 5 – сумма.
Сложение натуральных чисел выполняется по следующим правилам:
- Сложение производится слева направо, начиная с разряда единиц;
- Если сумма цифр в одном разряде больше 9, переносим единицу в следующий разряд;
- При наличии переноса в старший разряд, он также учитывается в результате сложения.
Вычитание натуральных чисел
Вычитание натуральных чисел – это операция, при которой из одного числа вычитается другое число. Когда мы вычитаем натуральные числа, мы уменьшаем их значение.
Для вычитания натуральных чисел используется знак “-“. Например, 5 – 2 = 3, где 5 – уменьшаемое, 2 – вычитаемое, а 3 – разность.
Вычитание натуральных чисел выполняется по следующим правилам:
- Вычитание производится слева направо, начиная с разряда единиц;
- Если значение вычитаемого равно или больше значения уменьшаемого, исходное число обнуляется;
- При наличии заема из старшего разряда, он также учитывается в результате вычитания.
Сложение и вычитание натуральных чисел являются основой для выполнения других арифметических операций и решения математических задач. Понимание этих операций позволяет нам проводить точные вычисления и анализировать числовые данные.
Ответы к стр. 43
На 43 странице данного документа представлены ответы на поставленные вопросы. Ниже представлены краткие ответы к каждому вопросу:
Вопрос №1:
Что такое вычитание числа из суммы?
Ответ: Вычитание числа из суммы – это операция математического вычитания, при которой одно число вычитается из суммы других чисел.
Вопрос №2:
Как формулировалось свойство вычитания числа из суммы в учебнике?
Свойство вычитания числа из суммы гласит: “Вычесть число из суммы равносильно вычесть это число из каждого слагаемого и записать разность”.
Вопрос №3:
Как можно еще сформулировать свойство вычитания числа из суммы?
Ответ: Свойство вычитания числа из суммы также можно сформулировать следующим образом: “Вычитание числа из суммы равносильно уменьшению каждого слагаемого на это число и вычислению разности.”
Вопрос №4:
Как применить свойство вычитания числа из суммы на примере чисел 5, 3 и 2?
Ответ: Применение свойства вычитания числа из суммы на примере чисел 5, 3 и 2 означает, что вычитаемое число (например, 2) будет вычтено из каждого слагаемого (5 и 3), и полученные разности будут сложены: (5-2) + (3-2) = 3 + 1 = 4.
Вопрос №5:
Какое значение получилось при применении свойства вычитания числа из суммы на примере чисел 5, 3 и 2?
Ответ: При применении свойства вычитания числа из суммы на примере чисел 5, 3 и 2 получилось значение равное 4.
Свойство вычитания равных натуральных чисел
Определение:
Свойство вычитания равных натуральных чисел заключается в том, что результатом вычитания любого натурального числа из суммы равных натуральных чисел будет каждый раз именно это самое число, которое вычиталось, то есть разность будет равна этому числу.
Формулировка:
Пусть даны два равных натуральных числа a и b.
a = b
Тогда результатом вычитания числа a из суммы равных натуральных чисел будет число a.
a + a – a = a
Пример:
| a | b | Результат вычитания |
|---|---|---|
| 3 | 3 | 3 + 3 – 3 = 3 |
| 5 | 5 | 5 + 5 – 5 = 5 |
| 7 | 7 | 7 + 7 – 7 = 7 |
Таким образом, свойство вычитания равных натуральных чисел является аксиомой арифметики, которая позволяет нам точно определить результат вычитания в данном случае. Это свойство можно использовать при решении различных задач и упрощении выражений с вычитанием.
Переместительный закон (не выполняется для вычитания)
Вычитание является обратной операцией сложения, и поэтому переместительный закон, который применим для операции сложения, не применим для операции вычитания. Чтобы лучше понять, почему переместительный закон не выполняется при вычитании, рассмотрим его формулировку и применение к этой операции.
Переместительный закон для сложения
Переместительный закон для сложения гласит, что порядок слагаемых не влияет на итоговую сумму. Другими словами, можно менять местами слагаемые, и результат сложения будет одинаковым:
a + b = b + a
Это свойство удобно в использовании при совершении сложения, поскольку позволяет упростить вычисления и сделать их более гибкими.
Переместительный закон для вычитания
В отличие от сложения, переместительный закон не выполняется для операции вычитания. Если изменить порядок вычитаемых чисел, итоговый результат будет разным:
| Формулировка | Пример | Результат |
|---|---|---|
| a – b ≠ b – a | 5 – 3 ≠ 3 – 5 | 2 ≠ -2 |
Это означает, что при вычитании порядок вычитаемых чисел имеет значение и влияет на итоговый результат. Переместительный закон для вычитания не применим, и мы не можем просто поменять местами вычитаемые числа, чтобы получить эквивалентный результат. Вместо этого, при вычитании необходимо соблюдать определенный порядок действий.
Переместительный закон является важным свойством арифметических операций, но в случае вычитания он не выполняется. Порядок вычитаемых чисел оказывает существенное влияние на итоговый результат. Поэтому при выполнении вычитания необходимо соблюдать порядок действий и не менять местами вычитаемые числа.
Вычитание суммы двух чисел из натурального числа
Формула для вычитания суммы
Формула для вычитания суммы двух чисел из натурального числа выглядит следующим образом:
Разность = Натуральное число – (Первое число + Второе число)
Пример использования свойства
Рассмотрим пример, чтобы лучше понять, как работает это свойство. Предположим, у нас есть натуральное число 10, и нам нужно вычесть сумму двух чисел: 3 и 4.
Используя формулу, мы можем вычислить разность следующим образом:
| Натуральное число: | 10 |
| Первое число: | 3 |
| Второе число: | 4 |
| Сумма: | 3 + 4 = 7 |
| Разность: | 10 – 7 = 3 |
Таким образом, разность между натуральным числом 10 и суммой чисел 3 и 4 равна 3.
Свойство вычитания суммы двух чисел из натурального числа позволяет нам определить разность между этими числами. Оно является важной составляющей арифметики и помогает нам решать разнообразные математические задачи.
Вычитание числа из суммы
Вычитание числа из суммы имеет следующие свойства:
1. Коммутативность
Вычитание числа из суммы обладает свойством коммутативности, то есть порядок чисел не влияет на результат операции. Независимо от того, какие числа вы вычитаете из суммы, результат будет один и тот же. Например, a – (b + c) = (a – b) – c.
2. Ассоциативность
Вычитание числа из суммы также обладает свойством ассоциативности, то есть вы можете группировать числа по-разному без изменения результата. Например, (a – b) – c = a – (b + c).
3. Идемпотентность
Идемпотентность – это свойство операции, согласно которому повторное применение этой операции к тому же операнду не изменяет его значение. В случае вычитания числа из суммы, если вы несколько раз вычитаете одно и то же число, результат останется неизменным. Например, (a – b) – b = a – b.
4. Отсутствие обратного элемента
Вычитание числа из суммы не имеет обратного элемента, то есть нельзя точно определить, какое число нужно прибавить к сумме, чтобы получить начальное число. Например, для уравнения a + b = c, нельзя однозначно определить b, если известны только a и c.
Вычитание числа из суммы является важной операцией в математике и находит применение во многих областях, включая финансы, статистику, программирование и т.д. Понимание свойств вычитания числа из суммы помогает выполнять вычисления и анализировать данные более эффективно.
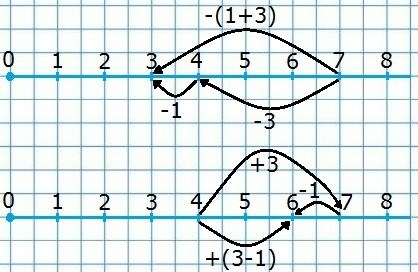
Вычитание на координатном луче
Вычитание на координатном луче представляет собой процесс уменьшения одного числа на величину другого числа на числовой оси. В данном контексте, координатный луч воспринимается как ось, на которой отмечены числа. Вычитание на координатном луче имеет своеобразные свойства, которые помогают нам понять и упростить этот процесс.
Свойство вычитания на координатном луче
Свойство вычитания на координатном луче заключается в том, что при вычитании числа из суммы двух чисел, можно вычесть это число из каждого слагаемого отдельно и сложить полученные результаты. Например, для вычисления разности между числами 7 и 3, можно вычесть 3 из 7 и получить 4, или вычесть 3 из 3 и получить 0. Затем, сложив результаты, получим 4.
Пример вычитания на координатном луче
Допустим, у нас есть два числа на координатном луче: 8 и 2. Для нахождения разности между этими числами, можно следовать следующим шагам:
- Вычитаем 2 из 8 и получаем 6.
- Вычитаем 2 из 2 и получаем 0.
- Складываем результаты: 6 + 0 = 6.
Таким образом, разность между числами 8 и 2 равна 6.
Таблица вычитания на координатном луче
| Уменьшаемое | Вычитаемое | Разность |
|---|---|---|
| 10 | 4 | 6 |
| 5 | 2 | 3 |
| 12 | 8 | 4 |
В таблице приведены примеры вычитания на координатном луче. Уменьшаемое число вычитается из каждого вычитаемого числа, а затем полученные разности складываются для получения окончательного результата.
Вычитание на координатном луче является важным математическим процессом, который позволяет нам находить разность между числами на оси. Свойство этого вид вычитания упрощает процесс вычислений и помогает нам лучше понять его суть.
Часто задаваемые вопросы
В этом разделе мы собрали ответы на некоторые наиболее часто задаваемые вопросы о свойстве вычитания числа из суммы.
1. Как формулируется свойство вычитания числа из суммы?
Свойство вычитания числа из суммы формулируется следующим образом:
“Результат вычитания числа из суммы равен разности между каждым слагаемым суммы и вычитаемым числом.”
2. Как это свойство может быть полезно в математике?
Свойство вычитания числа из суммы является основой для решения различных математических задач. Оно помогает нам вычислять разности чисел и выполнять операции с вычитанием.
3. Как применить свойство вычитания числа из суммы в практических задачах?
Для применения свойства вычитания числа из суммы в практических задачах нужно следовать формулировке свойства и последовательно вычислять разности каждого слагаемого суммы и вычитаемого числа. Это позволит нам получить результат вычитания.
4. Как проверить правильность работы свойства вычитания числа из суммы?
Для проверки правильности работы свойства вычитания числа из суммы можно выполнить обратную операцию – сложение результатов вычитаний каждого слагаемого и вычитаемого числа. Если сумма этих результатов будет равна исходной сумме, то свойство вычитания числа из суммы было применено правильно.
5. Можно ли применять свойство вычитания числа из суммы для других операций?
Нет, свойство вычитания числа из суммы применимо только для операции вычитания. Для других операций (сложение, умножение, деление) существуют свои специфические свойства, которые необходимо применять.
В данной статье мы рассмотрели свойство вычитания числа из суммы, его формулировку, способы применения и проверки. Надеемся, что эта информация была полезной и поможет вам лучше понять и использовать это свойство в математических задачах.