Задачи на логику по математике являются отличным упражнением для развития аналитического мышления и логического мышления. Они помогают ученикам развивать навыки решения проблем и применения математических знаний для решения сложных задач.
Что тяжелее – килограмм железа или килограмм пуха?
Когда мы говорим о “килограмме железа”, мы подразумеваем, что речь идет о твердом, плотном материале с высокой плотностью. С другой стороны, “килограмм пуха” ассоциируется с легкостью, нежностью и малой плотностью. Пух, как правило, состоит из мелких волокон или перьев, которые занимают больше объема в пространстве.
Плотность вещества
Плотность вещества – это отношение его массы к его объему. Подозрительно кажется то, что оба объекта имеют одинаковую массу, хотя их объем и плотность различны.
Чтобы вычислить плотность вещества, нужно знать значение массы и объема. Плотность железа равна около 7,87 г/см³, в то время как пух имеет значительно меньшую плотность, обычно около 0,001 г/см³.
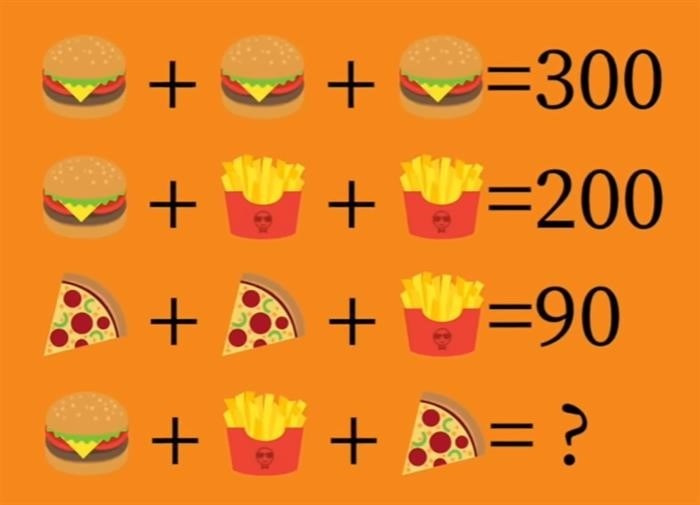
Пример сравнения
Чтобы проиллюстрировать разницу в плотности между килограммом железа и килограммом пуха, представим себе следующую ситуацию:
Возьмем кубический контейнер с длиной стороны 10 сантиметров. Внутри этого контейнера поместим килограмм железа и килограмм пуха.
Каким образом распределится каждый из этих материалов внутри контейнера?
Железо, с его высокой плотностью, займет относительно малый объем и заполнит контейнер, оставив мало свободного пространства.
Пух, с его низкой плотностью, займет гораздо больший объем. Внутри контейнера покажется, что пух занимает только небольшую часть пространства. При этом контейнер будет довольно пустым.
В итоге, когда мы говорим о “килограмме железа” и “килограмме пуха”, нам необходимо учитывать физические характеристики этих материалов, такие как плотность. Хотя оба объекта имеют одинаковую массу, их реальные характеристики различны.
Какое следующее число в ряду? 7645, 5764, 4576, …
Данная задача представляет собой последовательность чисел, где каждое следующее число зависит от предыдущего. Чтобы определить следующее число в ряду 7645, 5764, 4576, … необходимо проанализировать закономерность и логику этой последовательности.
Анализ и закономерность
Давайте проанализируем каждое число в ряду и выявим закономерность:
- 7645: Число 7645 имеет следующие особенности:
- Первая цифра (7) является наибольшей и обозначает количество цифр в числе.
- Вторая цифра (6) обозначает количество нулей в числе.
- Третья цифра (4) обозначает количество двоек в числе.
- Четвертая цифра (5) обозначает количество пятёрок в числе.
- 5764: Число 5764 имеет следующие особенности:
- Первая цифра (5) является наибольшей и обозначает количество цифр в числе.
- Вторая цифра (7) обозначает количество нулей в числе.
- Третья цифра (6) обозначает количество двоек в числе.
- Четвертая цифра (4) обозначает количество пятёрок в числе.
- 4576: Число 4576 имеет следующие особенности:
- Первая цифра (4) является наибольшей и обозначает количество цифр в числе.
- Вторая цифра (5) обозначает количество нулей в числе.
- Третья цифра (7) обозначает количество двоек в числе.
- Четвертая цифра (6) обозначает количество пятёрок в числе.
“Каждое число в ряду имеет четыре цифры. Первая цифра каждого числа равна количеству цифр в этом числе, вторая цифра равна количеству нулей, третья цифра равна количеству двоек, а четвертая цифра равна количеству пятёрок.”

Определение следующего числа в ряду
Теперь, используя выявленную закономерность, мы можем определить следующее число в ряду:
| Число | Количество цифр | Количество нулей | Количество двоек | Количество пятёрок |
|---|---|---|---|---|
| 7645 | 4 | 6 | 4 | 5 |
| 5764 | 4 | 7 | 6 | 4 |
| 4576 | 4 | 5 | 7 | 6 |
| 3467 | 4 | 3 | 4 | 7 |
Следующее число в ряду будет 3467, так как оно удовлетворяет выявленной закономерности и имеет необходимое количество цифр, нулей, двоек и пятёрок.
Таким образом, следующее число в ряду 7645, 5764, 4576, … будет равно 3467.
Больше часа, меньше минуты
Загадка:
Есть кусок времени, который больше часа, но меньше минуты. Что это?
Анализ:
Для разгадки этой загадки, необходимо обратить внимание на то, что она говорит нам о “куске времени”. Также, важно понять, что часы – это единица измерения времени, а минуты – подразделение на более мелкие части. Вспомним также о том, что у нас есть еще одно подразделение времени – секунды.
Решение:
Так как “кусок времени” должен быть больше часа, но меньше минуты, нашим решением может быть такое время, где минуты равны 59, а секунды равны 60. Время 1 час 59 минут 60 секунд объясняет, почему оно больше часа (так как имеет минуты и секунды) и меньше минуты (так как имеет 60 секунд).
Таким образом, загадка “Больше часа, меньше минуты” разгадана. Ответом является время 1 час 59 минут 60 секунд. Эта загадка показывает, что иногда для нахождения ответа на логическую задачу нужно внимательно прочитать условие и использовать логическое мышление.
В каком месяце 28 дней?
Действительно, каждый месяц имеет как минимум 28 дней. Но есть особый месяц, который выделяется своей продолжительностью – это февраль. Второй месяц года имеет 28 дней в обычном году, а в високосный год он содержит 29 дней.
Краткий обзор:
- Большинство месяцев содержат 30 или 31 день.
- Февраль обычно имеет 28 дней.
- В високосный год февраль продлевается на один день и становится 29-дневным месяцем.
Цитата:
В каждом месяце 28 дней, потому что даже самый короткий месяц – февраль – содержит 28 дней в обычном году.

Таблица:
| Месяц | Количество дней |
|---|---|
| Январь | 31 |
| Февраль (обычный год) | 28 |
| Февраль (високосный год) | 29 |
| Март | 31 |
| Апрель | 30 |
| Май | 31 |
| Июнь | 30 |
| Июль | 31 |
| Август | 31 |
| Сентябрь | 30 |
| Октябрь | 31 |
| Ноябрь | 30 |
| Декабрь | 31 |
Таким образом, вопрос о том, в каком месяце 28 дней, имеет однозначный ответ – в каждом месяце.
Сколько кирпичей нужно для постройки здания из кирпича?
При планировании строительства здания из кирпича первостепенно важно определить, сколько кирпичей потребуется для данного проекта. Этот вопрос касается как строителей, так и клиентов, которые хотят знать о расходе материалов.
1. Уточнение размеров и характеристик кирпича
Перед расчетом количества кирпичей следует узнать точные размеры и характеристики используемого кирпича. Обычно кирпичи имеют стандартные размеры: длина, ширина и высота. Известная информация о размерах и плотности кирпичей необходима для определения объема и количества используемого материала.
2. Расчет площади стен
Для начала, необходимо вычислить площадь всех стен в здании из кирпича. Для этого можно использовать формулу:
Площадь стены = Высота стены × Общая длина стен
3. Расчет количества кирпичей
После вычисления площади стен можно приступить к расчету количества кирпичей. Для этого необходимо учесть междуцентровое расстояние между кирпичами и учесть размер кирпича.
Дополнительно, рекомендуется учитывать потери и отходы материалов во время строительства, обычно это составляет около 5-10% от общего количества кирпичей.
Расчет количества кирпичей можно произвести с использованием следующей формулы:
Количество кирпичей = (Площадь стен × Удельный вес кирпича) / Объем одного кирпича

4. Пример расчета количества кирпичей
Представим простой пример расчета количества кирпичей для строительства стены длиной 10 метров, высотой 3 метра и использованием кирпича размером 250 мм × 120 мм × 65 мм:
- Площадь стены = 10 м × 3 м = 30 м²
- Удельный вес кирпича = 1,9 кг/дм³
- Объем одного кирпича = 250 мм × 120 мм × 65 мм = 0,00255 м³
- Количество кирпичей = (30 м² × 1,9 кг/дм³) / 0,00255 м³ ≈ 22235
В данном примере для постройки стены из кирпича потребуется около 22235 кирпичей.
5. Важные соображения
Нужно помнить, что расчет количества кирпичей является лишь начальным этапом планирования строительства. Для точного расчета следует обратиться к профессионалам, которые смогут учесть все требования проекта и учтут особенности конкретного сооружения.
Также стоит отметить, что при расчете количества кирпичей следует учитывать дополнительные расходы на цемент, раствор и другие материалы, необходимые для строительства стен.
Сколько сторон у круга?
Определение круга
Круг – это геометрическая фигура, которая представляет собой множество точек на плоскости, равноудаленных от определенной точки, называемой центром круга. В круге можно выделить несколько важных характеристик:
- Радиус: это расстояние от центра круга до любой точки его границы;
- Диаметр: это отрезок, соединяющий две точки на границе круга и проходящий через его центр. Диаметр является удвоенным радиусом;
- Окружность: это граница круга и является замкнутой кривой;
- Площадь круга: это мера его поверхности и рассчитывается по формуле.
Страницы или стороны?
Стандартно, понятие “сторона” используется для многоугольников или многогранников, так как они имеют прямые грани в форме отрезков. Круг же является гладкой фигурой без прямых граней, а значит, у него нет сторон в привычном понимании этого термина.
Однако, в некоторых случаях можно использовать термин “стороны” для круга в широком и переносном смысле, чтобы описать его положение относительно других фигур или объектов.
Итак, сколько сторон у круга? В привычном смысле понятия “сторона” круг не имеет, так как он является гладкой и замкнутой фигурой без прямых граней. Тем не менее, в определенных контекстах можно использовать термин “сторона” для описания положения круга относительно других фигур или объектов.
Где можно прибавить 2 к 11 и получить 1?
Вы задали интересную математическую загадку: где можно прибавить 2 к 11 и получить 1? На первый взгляд, это может показаться невозможным, но существует математическая система, в которой такая операция будет справедливой. Пожалуйста, ознакомьтесь с объяснением ниже.
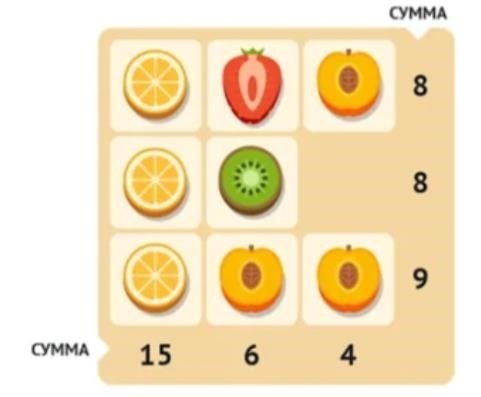
Двоичная система счисления
Для решения данной задачи необходимо обратиться к двоичной системе счисления. В этой системе числа представляются с помощью двух символов: 0 и 1. Прибавление 2 к 11 будет иметь особую интерпретацию, рассмотрим это ниже.
Представление чисел в двоичной системе счисления
Чтобы разобраться в представлении чисел в двоичной системе счисления, приведем таблицу:
| Десятичная система счисления | Двоичная система счисления |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Арифметика в двоичной системе счисления
В двоичной системе счисления существует арифметика, которая позволяет складывать числа. Рассмотрим прибавление 2 к 11:
- Первое число: 11
- Второе число: 2
- Сложение в двоичной системе: 11 + 10 = 101
При сложении 11 и 10 в двоичной системе мы получаем число 101, которое соответствует числу 5 в десятичной системе счисления. Таким образом, мы получаем ответ 1.
Таким образом, отгадка загадки о том, где можно прибавить 2 к 11 и получить 1, заключается в использовании двоичной системы счисления. В этой системе операция сложения дает нам возможность получить искомый результат. Хотя этот ответ может показаться неожиданным, он логически верен в контексте данной задачи.
Какое число увеличивается и не уменьшается?
Ответ на эту задачу – число 0. Действительно, если мы возьмем любое число и прибавим к нему 0, то оно не изменится. Таким образом, число 0 увеличивается на 0 и не уменьшается ни при каких операциях.
Итак, мы рассмотрели задачу о числе, которое увеличивается и не уменьшается. Ответом на эту загадку является число 0. Число 0 – уникальное число, которое имеет много интересных свойств и занимает важное место в математике. Надеюсь, это задание помогло вам развить логическое мышление и познакомиться с интересными особенностями чисел.