Вычитание обыкновенных дробей с разными знаменателями – это математическая операция, при которой происходит вычитание одной обыкновенной дроби от другой, при условии, что у них разные знаменатели. Для выполнения данной операции необходимо привести дроби к общему знаменателю, а затем вычесть числители. Полученную разность можно упростить, если необходимо.
Свойства вычитания при работе с дробями
Свойство 1: Общий знаменатель
Для выполнения вычитания дробей с разными знаменателями необходимо найти их общий знаменатель. Общий знаменатель является наименьшим общим кратным знаменателей исходных дробей. Поиск общего знаменателя позволяет свести дроби к одному и тому же знаменателю и сделать их сравнимыми.
Свойство 2: Вычитание числителей
После нахождения общего знаменателя обратите внимание на числители дробей. Вычитайте числители как обычные числа, учитывая знаки. Если дроби имеют одинаковый знак, вычитание их числителей сводится к вычитанию обычных чисел. Если дроби имеют разные знаки, вычитание числителей производится по обычным правилам вычитания с учетом знака.
Свойство 3: Упрощение дроби
Полученный результат после вычитания числителей может быть несократимой дробью. Для упрощения дроби необходимо найти их наибольший общий делитель и поделить числитель и знаменатель на него. Упрощение дроби позволяет представить ее в наиболее простом виде.

Приведенные свойства помогают правильно выполнять операцию вычитания при работе с дробями с разными знаменателями. Используйте эти свойства для упрощения вычислений и получения точного результата.
Вычитание натурального числа из обыкновенной дроби
При выполнении арифметических операций с обыкновенными дробями важно знать, как вычитать натуральное число из дроби. Процесс вычитания такого числа из дроби можно разбить на несколько шагов.
Шаг 1: Приведение знаменателя к общему кратному для обоих слагаемых
Для начала нужно найти общий знаменатель для обыкновенной дроби и натурального числа. Для этого нужно найти наименьшее общее кратное (НОК) знаменателя дроби и 1 (так как натуральные числа не имеют знаменателя).
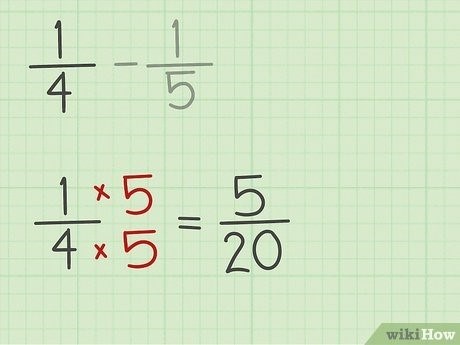
Шаг 2: Приведение обыкновенной дроби к новому знаменателю
После нахождения общего знаменателя необходимо привести обыкновенную дробь к новому знаменателю. Для этого умножаем числитель и знаменатель дроби на такое число, чтобы знаменатель стал равен общему знаменателю.
Шаг 3: Вычитание натурального числа
После приведения дроби к новому знаменателю, можно приступить к самому вычитанию. Для этого от числителя дроби вычитаем значение натурального числа.
Пример:
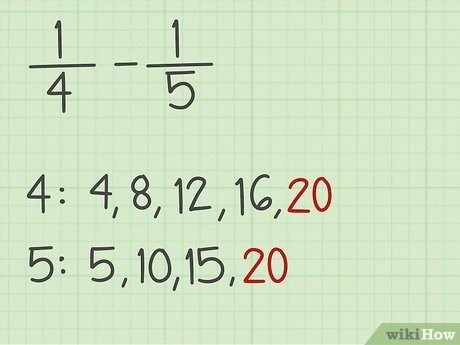
| 4 | |
| – | 2 |
| 2 |
В результате получаем новую обыкновенную дробь с измененным числителем и замененным знаменателем. В данном примере результатом является дробь 2/2, которая равна целому числу 1.
Вычитание смешанных чисел
Правила выполнения операции вычитания смешанных чисел:
- Вычитать целые части чисел;
- Вычитать дробные части чисел;
- Если результат вычитания дробных частей отрицателен, то нужно заемствовать единицу от целой части числа, а затем вычесть дробные части чисел.
Пример:
Вычтем число 4 1/2 из числа 7 3/4:
- Вычитаем целые части чисел: 7 – 4 = 3;
- Вычитаем дробные части чисел: 3/4 – 1/2;
- Для вычитания дробей с разными знаменателями нам нужно привести их к общему знаменателю. В данном случае это 4.
- Вычитание дробей: (3*2 – 1*3) / 4 = 6/4 – 3/4 = 3/4.
| Дроби | Вычитание |
|---|---|
| 3/4 | – 1/2 |
Итак, результат вычитания числа 4 1/2 из числа 7 3/4 равен 3 3/4.
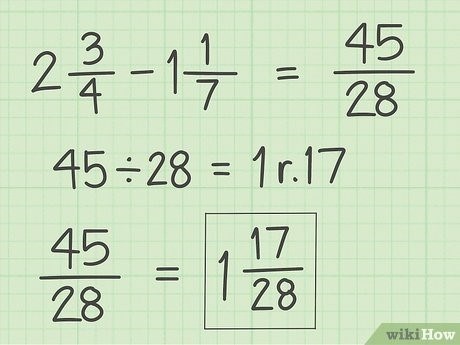
Об этой статье
В данной статье мы рассмотрели методы вычитания обыкновенных дробей с разными знаменателями. Мы начали с изучения операций с обыкновенными дробями, включая их общий вид и правила сокращения.
Затем мы перешли к вычитанию обыкновенных дробей. Показали, как сравнить знаменатели, и если они различаются, привести дроби к общему знаменателю с помощью метода наименьшего общего кратного.
Мы ознакомились с алгоритмом вычитания дробей после приведения их к общему знаменателю. В конечном итоге мы поняли, что результат вычитания обыкновенных дробей с разными знаменателями также является обыкновенной дробью.
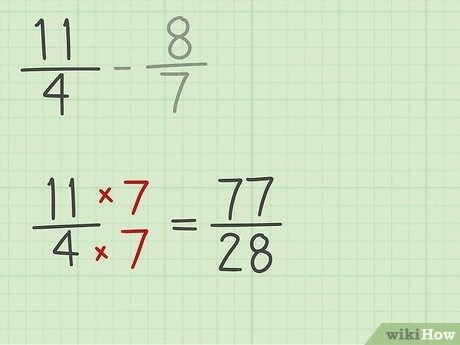
В этой статье мы рассмотрели основы вычитания обыкновенных дробей с разными знаменателями. Используя эти методы, вы сможете успешно выполнять вычитание таких дробей и решать соответствующие математические проблемы.