Определение расстояния от точки до плоскости – одна из основных задач аналитической геометрии. Координатный метод позволяет вычислить это расстояние с использованием координат точки и уравнения плоскости. Он основан на формуле, которая представляет собой отношение модуля суммы коэффициентов уравнения плоскости к квадратному корню из суммы квадратов этих коэффициентов. Этот метод является универсальным и может быть использован для решения различных задач, связанных с геометрией пространства.
1. Расстояние между двумя точками
Для вычисления расстояния между двумя точками можно использовать координатный метод, основанный на координатах этих точек. Формула для вычисления расстояния также известна и широко применяется:
Формула расстояния между двумя точками:
√((x2 – x1) 2 + (y2 – y1) 2)
Где:
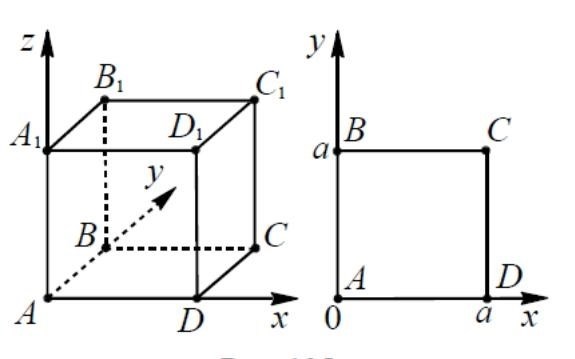
- (x1, y1) – координаты первой точки
- (x2, y2) – координаты второй точки
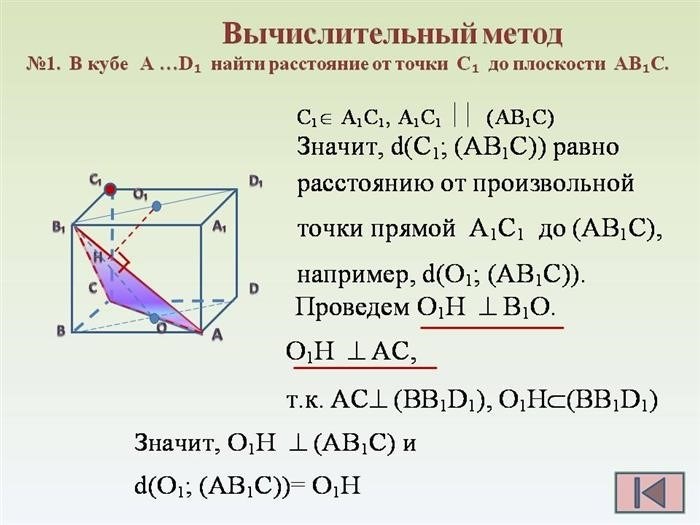
Эта формула позволяет найти длину отрезка между двумя точками на плоскости. Результатом является положительное число, которое показывает, насколько далеко эти точки находятся друг от друга.
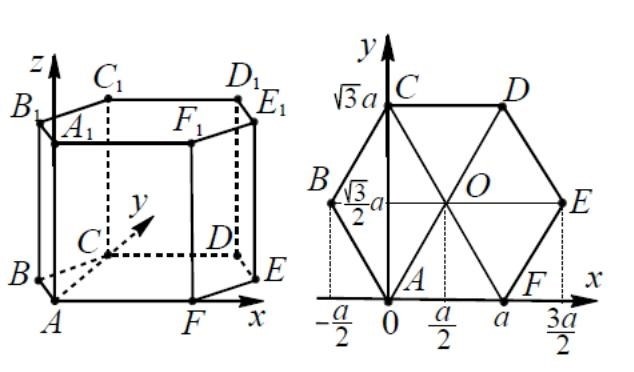
Подписи к слайдам
На протяжении всей презентации мы рассмотрели различные аспекты расстояния от точки до плоскости с использованием координатного метода. В этом разделе мы подведем итоги и обобщим полученные результаты.

В ходе изучения данной темы мы разобрали следующие ключевые моменты:

- Определение понятия “расстояние от точки до плоскости” и перечисление основных задач, связанных с ним;
- Рассмотрение основных шагов для нахождения расстояния от точки до плоскости методом проекций;
- Объяснение применения формулы для расчета расстояния между точкой и плоскостью;
- Приведение примеров, иллюстрирующих решение задач на нахождение расстояния от точки до плоскости;
- Анализ особенностей и ограничений данного метода расчета;
Важно помнить, что использование координатного метода позволяет точно определить расстояние от точки до плоскости на основе известных координат точки и параметров плоскости. При этом, следует учитывать особенности задачи и правильно применять метод проекций или формулу, чтобы получить верный результат.

Знание данной темы позволяет углубить понимание геометрических взаимосвязей и применять полученные знания для решения различных практических задач.