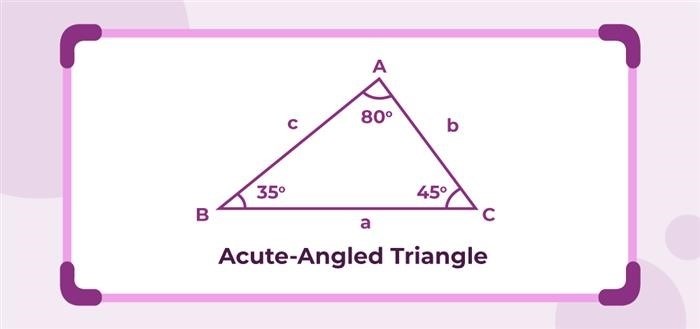
Равносторонний треугольник – это треугольник, у которого все стороны и углы равны. Остроугольным треугольником называется треугольник, у которого все углы острые. Всякий равносторонний треугольник является остроугольным, так как все его углы меньше 90 градусов.
Остроугольный треугольник: элементы, свойства, признаки и формулы
Элементы остроугольного треугольника:
- Стороны: треугольник состоит из трех сторон, которые могут быть разной длины.
- Углы: треугольник имеет три острых угла, каждый из которых меньше 90 градусов.
- Высоты: остроугольный треугольник также имеет три высоты, которые можно опустить из каждой вершины на противолежащую сторону.
- Медианы: треугольник имеет три медианы, которые соединяют каждую вершину с серединой противолежащей стороны.
- Биссектрисы: остроугольный треугольник имеет также три биссектрисы, которые делят каждый угол на две равные части.
Свойства остроугольного треугольника:
- Все три внутренних угла острогоугольного треугольника являются острыми, то есть меньше 90 градусов.
- Сумма углов остроугольного треугольника равна 180 градусам.
- Остроугольный треугольник может быть равносторонним, то есть иметь равные стороны и равные углы.
- Высоты, медианы и биссектрисы остроугольного треугольника пересекаются в одной точке – центре вписанной окружности.
Формулы для остроугольного треугольника:
Пусть a, b и c – стороны остроугольного треугольника, а A, B и C – соответствующие острые углы.
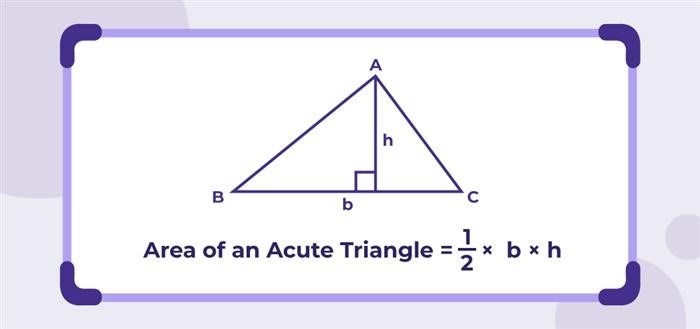
- Формула для площади треугольника: S = 0.5 * a * b * sin(C).
- Теорема косинусов: c 2 = a 2 + b 2 – 2ab * cos(C).
- Теорема синусов: a/sin(A) = b/sin(B) = c/sin(C).
- Формула для радиуса вписанной окружности: r = (a + b + c) / (4 * S), где S – площадь треугольника.
Остроугольный треугольник – это треугольник, у которого все три угла острые и меньше 90 градусов. Он обладает свойством равномерного распределения углов и может быть равносторонним. Для вычисления его свойств и параметров, можно использовать различные формулы, такие как формулы для площади, радиуса вписанной окружности и теоремы косинусов и синусов. Остроугольные треугольники широко используются в геометрии, физике и других науках.
Остроугольный треугольник: понятие и определение
Основные характеристики остроугольного треугольника:
- Углы треугольника: Каждый угол остроугольного треугольника меньше 90 градусов. Сумма всех углов треугольника всегда равна 180 градусов.
- Стороны треугольника: Все стороны остроугольного треугольника положительны и они не равны друг другу. Длина каждой стороны может быть различной, но должна удовлетворять неравенству треугольника.
- Высоты и медианы: Остроугольный треугольник имеет три высоты, которые проведены из каждой вершины к противоположной стороне. Медианы также проводятся из каждой вершины к середине противоположной стороны.
Свойства остроугольного треугольника:
- Точка пересечения высот: В остроугольном треугольнике высоты пересекаются в одной точке, называемой ортоцентром. Ортоцентр остроугольного треугольника лежит внутри треугольника.
- Угол между высотой и основанием: Угол между высотой и основанием в остроугольном треугольнике всегда острый, так как основание является стороной треугольника, а высота проходит через его вершину.
- Основание медианы и средняя линия: В остроугольном треугольнике основание каждой медианы и средней линии является серединой противоположной стороны.
| Свойство | Описание |
|---|---|
| Точка пересечения высот | Высоты пересекаются в ортоцентре |
| Угол между высотой и основанием | Острый угол |
| Основание медианы и средняя линия | Середина противоположной стороны |
Важные термины треугольника
Внутренний угол треугольника – это угол, образованный двумя сторонами треугольника внутри самого треугольника. Сумма всех внутренних углов треугольника равна 180 градусам.
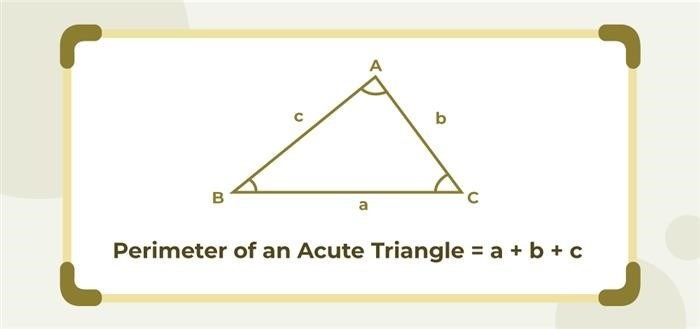
Остроугольный треугольник
Остроугольный треугольник – это треугольник, у которого каждый из его внутренних углов является остроугольным. Острый угол – это угол, меньший 90 градусов.
Всякий равносторонний треугольник является остроугольным. Равносторонний треугольник – это треугольник, у которого все стороны равны друг другу.
Итог
- Треугольник – геометрическая фигура, образованная тремя сторонами.
- Внутренний угол треугольника – угол, образованный двумя сторонами треугольника внутри самого треугольника.
- Остроугольный треугольник – треугольник, у которого каждый из его внутренних углов является остроугольным.
- Равносторонний треугольник – треугольник, у которого все стороны равны друг другу.
Теперь вы знакомы с основными терминами, связанными с треугольниками. Используя эти термины, вы сможете легче понимать и описывать треугольники в геометрии.