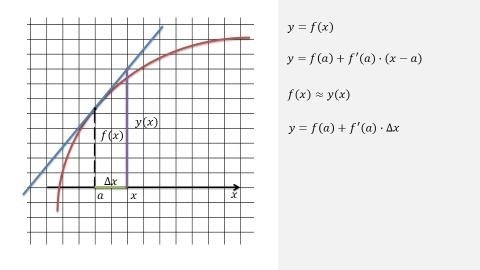
Уравнение касательной к графику функции – это математическое соотношение, описывающее прямую, которая касается графика функции и имеет с ним общую точку. Касательная является одной из важных характеристик графика функции и позволяет определить его наклон и поведение в данной точке. Уравнение касательной можно найти с помощью определения производной функции и используя координаты точки, в которой необходимо построить касательную.
Применение уравнения касательной в реальной жизни
Применение уравнения касательной в реальной жизни позволяет решать разнообразные задачи, такие как:
1. Оптимизация производства
Уравнение касательной может быть использовано для оптимизации производства. Например, в производстве автомобилей можно использовать уравнение касательной для определения оптимального угла наклона деталей, чтобы достичь максимальной эффективности и минимизации стоимости производства.
2. Прогнозирование финансовых рынков
Уравнение касательной может быть применено для прогнозирования финансовых рынков. Например, в инвестиционной сфере уравнение касательной может использоваться для определения точки пересечения цены акции и касательной, что помогает инвесторам принимать решения о покупке или продаже акций.
3. Анализ движения тела
Уравнение касательной может быть применено для анализа движения тела. Например, в физике уравнение касательной может использоваться для определения скорости тела в конкретный момент времени или для предсказания будущего положения тела на основе его текущей скорости и ускорения.

4. Оптимизация траекторий
Уравнение касательной может быть использовано для оптимизации траекторий. Например, в авиационной индустрии уравнение касательной может помочь пилотам определить оптимальную траекторию полета, которая минимизирует расход топлива и время в пути.
5. Разработка новых материалов
Уравнение касательной может быть применено в разработке новых материалов. Например, в инженерии и научных исследованиях уравнение касательной может использоваться для определения оптимальной структуры материала с целью улучшения его прочности, гибкости или других характеристик.
Свойства уравнения касательной
Уравнение касательной к графику функции имеет несколько важных свойств:
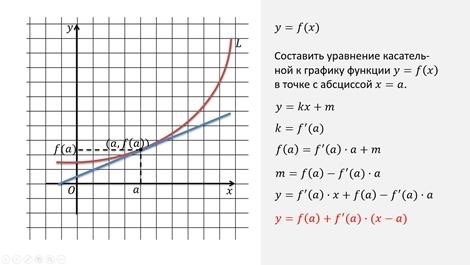
- Уравнение касательной определяет прямую, касающуюся графика функции в заданной точке. Это позволяет нам аппроксимировать поведение функции вблизи данной точки.
- Уравнение касательной может быть использовано для нахождения наклона касательной строки и определения производной функции в данной точке.
- Касательная к графику функции в точке имеет наклон, равный производной функции в этой точке. Таким образом, уравнение касательной позволяет нам определить значение производной функции в заданной точке.
- Уравнение касательной может быть использовано для нахождения точек пересечения графика функции с прямой. Для этого необходимо решить уравнение касательной и уравнение функции, приравнивая их друг к другу.
Итак, уравнение касательной является полезным инструментом для анализа поведения функции вблизи заданной точки и определения производной функции в этой точке. Оно позволяет нам получить информацию о наклоне функции и ее пересечениях с прямой. Это важные свойства, которые позволяют лучше понять и изучать функции и их поведение.