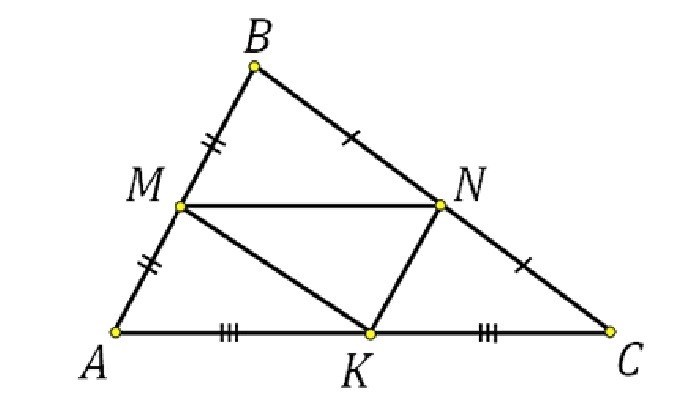
Теорема о средней линии треугольника – это геометрическое утверждение, которое гласит, что серединные линии треугольника делятся на три равные части. В математике серединные линии треугольника представляют собой отрезки, соединяющие середины его сторон. Эта теорема имеет множество применений и является одной из базовых концепций в геометрии.
Средняя линия прямоугольного треугольника
Средняя линия прямоугольного треугольника проходит через точку, которая является серединой гипотенузы и делит ее на две равные части.
Свойства средней линии прямоугольного треугольника:
- Средняя линия параллельна гипотенузе и равна половине ее длины
- Средняя линия является высотой и медианой треугольника одновременно
- Сумма длин катетов, проведенных от вершины прямого угла треугольника до точек пересечения средней линии с катетами, равна длине гипотенузы
Средняя линия прямоугольного треугольника может служить важным инструментом для решения различных задач и вычислений, связанных с треугольниками. Она помогает определить положение и свойства треугольника с учетом его геометрических параметров.
| Свойство | Описание |
|---|---|
| Средняя линия параллельна гипотенузе и равна половине ее длины | Средняя линия проходит через середину гипотенузы и делит ее пополам |
| Средняя линия является высотой и медианой треугольника одновременно | Средняя линия соединяет середины сторон и проходит через вершину прямого угла |
| Сумма длин катетов, проведенных от вершины прямого угла до точек пересечения средней линии с катетами, равна длине гипотенузы | Это следует из свойств подобных треугольников и применяется в решении задач на нахождение длины сторон треугольника |
Изучение свойств и использование средней линии прямоугольного треугольника позволяет более глубоко понять структуру и характеристики этой фигуры, а также применять их в практических задачах связанных с геометрией и тригонометрией.
Следствия из теоремы о средней линии треугольника
Теорема о средней линии треугольника предоставляет множество полезных и важных заключений и следствий. Рассмотрим некоторые из них с соответствующими доказательствами.
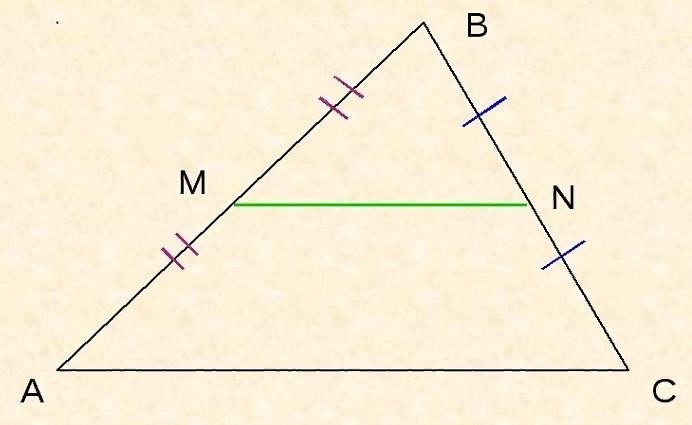
1. Средняя линия параллельна третьей стороне
Средняя линия треугольника, проведенная из вершины к середине противоположной стороны, параллельна третьей стороне.
Доказательство:
- Пусть ABC – треугольник, M – точка на стороне AB, а N – середина стороны BC.
- Проведем линию MN.
- Так как точка N – середина стороны BC, то BN=NC.
- В треугольнике BNC сторона BC общая, а сторона BN=NC.
- Поэтому треугольники BNM и CNM равнобедренные, и углы BNM и CNM равны.
- Также, угол BCM равен углу CNM, так как это углы-вертикальные.
- Из равенства углов BNM и CNM следует, что линия MN параллельна стороне BC.
2. Средние линии треугольника делятся пополам
Средние линии треугольника делятся пополам как по длине, так и по площади.
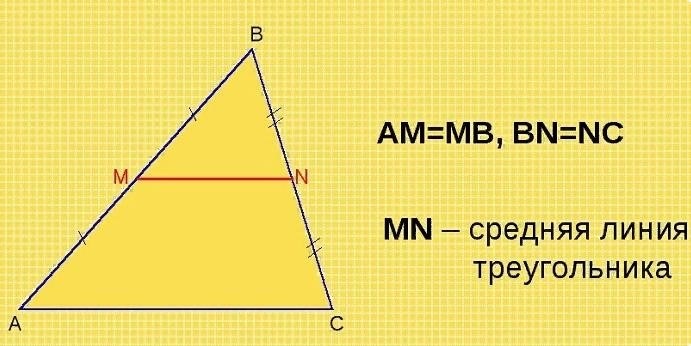
Доказательство:
- Пусть ABC – треугольник, M, N и P – точки, соединяющие середины сторон BC, AC и AB соответственно.
- Проведем линии MP и NP.
- Так как ширина прямоугольника равна половине его длины, а средние линии делят стороны пополам, то можно сказать, что MP=BC/2 и NP=AC/2.
- Также, так как P и N – середины сторон AB и AC соответственно, то PN равна половине длины стороны AB, то есть PN=AB/2.
- Из прямоугольного треугольника MPN следует, что площадь этого треугольника равна MP * PN / 2.
- Подставив значения MP, PN и BC/2, AC/2, AB/2 соответственно, получим, что площадь треугольника MPN равна площади треугольника ABC / 4.
- Таким образом, мы доказали, что средние линии треугольника делят стороны пополам и площадь треугольника делится ими на 4 равных части.
3. Сумма квадратов средних линий равна сумме квадратов сторон
Сумма квадратом длин средних линий треугольника равна сумме квадратов длин его сторон.
Доказательство:
- Пусть ABC – треугольник, M, N и P – точки, соединяющие середины сторон BC, AC и AB соответственно.
- Обозначим длины сторон треугольника ABC как a, b и c.
- Из известных свойств средних линий треугольника следует, что MP=BC/2, NP=AC/2 и PN=AB/2.
- Таким образом, квадрат длины средней линии MP равен (BC/2) 2, квадрат длины NP равен (AC/2) 2, а квадрат длины PN равен (AB/2) 2.
- Суммируя эти три квадрата, получаем (BC/2) 2 + (AC/2) 2 + (AB/2) 2.
- Раскрывая скобки, получим (BC 2 + AC 2 + AB 2) / 4.
- С другой стороны, квадрат длины стороны a равен a 2, квадрат длины стороны b равен b 2, а квадрат длины стороны c равен c 2.
- Суммируя эти три квадрата, получаем a 2 + b 2 + c 2.
- Таким образом, мы доказали, что сумма квадратов длин средних линий треугольника равна сумме квадратов длин его сторон.
Часто задаваемые вопросы:
1. Какая теорема описывает среднюю линию треугольника?
Средняя линия треугольника это отрезок, соединяющий середины двух его сторон. Теорема о средней линии треугольника утверждает, что средняя линия треугольника параллельна третьей стороне и составляет половину ее длины.

2. Как можно найти длину средней линии треугольника?
Для нахождения длины средней линии треугольника можно воспользоваться формулой:
Длина средней линии = (Длина первой стороны + Длина второй стороны) / 2
Здесь “Длина первой стороны” и “Длина второй стороны” – это длины соответствующих сторон треугольника.
3. Какие свойства имеет средняя линия треугольника?
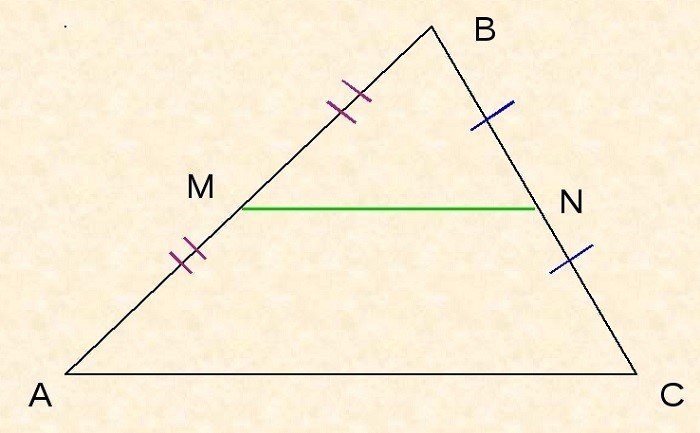
Средняя линия треугольника обладает следующими свойствами:
- Она соединяет середины двух сторон треугольника.
- Делит треугольник на две равные части по площади.
- Является параллельной третьей стороне треугольника и составляет с ней отношение 1:2.
4. Для каких треугольников выполняется теорема о средней линии?
Теорема о средней линии треугольника выполняется в любом треугольнике, независимо от его типа (равносторонний, равнобедренный, произвольный).
5. Какую роль играет средняя линия треугольника в геометрии?
Средняя линия треугольника является важной геометрической характеристикой треугольника. Она не только предоставляет информацию о равенстве половин длин треугольника, но также служит базой для других свойств и теорем треугольника.
Средняя линия треугольника: свойства, признаки и формулы
Свойства средней линии треугольника:
- Средняя линия треугольника параллельна третьей стороне и равна половине ее длины.
- Середина каждой стороны треугольника является точкой пересечения средних линий, проведенных из вершин, противоположных этим сторонам.
- Длина средней линии треугольника можно вычислить по формуле: l = 0.5 * s, где l – длина средней линии, s – длина стороны треугольника.
- Средняя линия треугольника делит его на два треугольника, площади которых равны.
Признаки средней линии треугольника:
- Если средняя линия треугольника проходит через вершину, то она делит треугольник на два треугольника равных площадей.
- Если средняя линия треугольника параллельна одной из его сторон, то она делит треугольник на два треугольника равных площадей.
Пример:
Дан треугольник ABC со сторонами a = 8, b = 10, c = 12.
Найдем длины средних линий треугольника:
- Средняя линия, соединяющая середину стороны AB с серединой стороны BC, имеет длину 6 и параллельна стороне AC.
- Средняя линия, соединяющая середину стороны AB с серединой стороны AC, имеет длину 4 и параллельна стороне BC.
- Средняя линия, соединяющая середину стороны BC с серединой стороны AC, имеет длину 7 и параллельна стороне AB.
Средняя линия треугольника является важным элементом, который позволяет решать задачи, связанные с треугольниками. Она обладает рядом свойств, которые помогают в вычислениях и нахождении площадей треугольников. Знание свойств средней линии треугольника позволяет более глубоко изучить его структуру и взаимосвязи между его элементами.
Деление отрезка на равные части
Итак, мы изучили способы деления отрезка на равные части. Начнем с того, что мы можем делить отрезок на любое заданное количество равных частей, используя способ с применением точек деления. Для этого необходимо провести линейку или масштабную линейку вдоль отрезка и отметить необходимое число равных отрезков на ней. Затем, используя циркуль или параллельно перемещаясь по ранее отмеченным точкам, мы можем разделить исходный отрезок на нужное количество равных частей.
Если нам необходимо разделить отрезок на равные части, но число частей не задано, мы можем использовать компас и линейку. Для этого мы проводим две окружности, центры которых лежат на концах отрезка, и пересекающиеся на одной точке. Затем, с использованием линейки, проводим линию через эту точку и конечные точки отрезка. Проводим еще две линии, параллельные первой, чтобы разделить отрезок на равные части, исходя из количества основных делений. Таким образом мы можем делить отрезок на любое количество равных частей.
Деление отрезка на равные части является важным инструментом в геометрии и математике в целом. Этот принцип находит применение в различных областях, таких как физика, архитектура и инженерное дело. Он помогает систематизировать и упростить задачи, связанные с делением отрезков и построением геометрических объектов.