Теорема о параллельных трех прямых утверждает, что если три прямые параллельны между собой, то все три пары соответствующих углов равны. Эта теорема базируется на аксиоме о параллельных прямых и имеет важное значение в геометрии, помогая решать различные задачи и доказывать другие теоремы.
Теорема о параллельных прямых, формулировка
Формулировка теоремы:
Если две прямые пересекаются с третьей прямой таким образом, что сумма внутренних углов по одну сторону от пересекающей прямой равна 180 градусам, то эти две прямые параллельны друг другу.
Примеры применения теоремы:
- При изучении треугольников и углов можно использовать теорему о параллельных прямых для доказательства параллельности определенных отрезков или линий.
- В геодезии теорема о параллельных прямых применяется для построения параллельных линий на плоскости или сфере.
- В архитектуре и строительстве теорема о параллельных прямых используется при построении параллельных стен, полов и потолков.
Доказательство теоремы:
1. Пусть AB и CD – две пересекающиеся прямые, и EF – третья прямая, пересекающая AB и CD.
2. Пусть угол AEF и угол CEF являются внутренними углами по одну сторону от прямой EF.
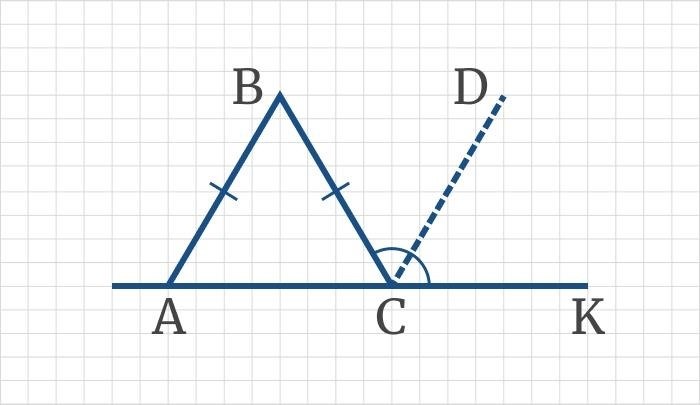
3. Согласно аксиоме о параллельных линиях, угол CEF равен внутреннему углу эквивалентного угла CEF’ в треугольнике AEF.
4. Сумма углов AEF и CEF равна 180 градусам.
5. Значит, угол AEF’ тоже равен 180 градусам (по свойству равенств).
6. Углы AEF’ и CEF’ являются внутренними углами треугольника AEF’.
7. Углы AEF’ и CEF’ вместе составляют 180 градусов.
8. Если две прямые, пересекающие третью прямую, образуют 180 градусов, то они параллельны (по определению параллельных прямых).
Лемма о двух параллельных прямых, пересекающих плоскость, и ее доказательство
Перед тем, как приступить к доказательству леммы о двух параллельных прямых, пересекающих плоскость, необходимо вспомнить несколько важных определений.
Определение: Плоскость – это геометрическая фигура, которая представляет собой неограниченную и самую тонкую поверхность без изгиба и изломов. В плоскости можно провести бесконечно много прямых.
Теперь перейдем к доказательству леммы:
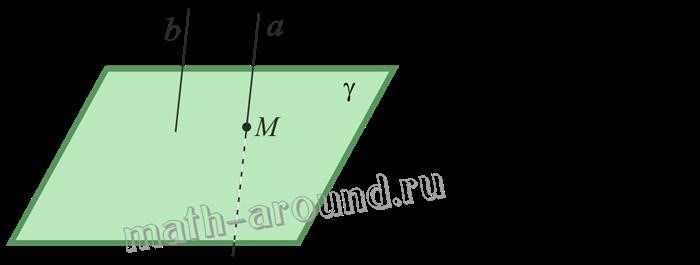
- Предположим, что у нас есть две параллельные прямые a и b, которые пересекают плоскость.
- Пусть точка пересечения прямых обозначается как O.
- Каждая из параллельных прямых, a и b, образует угол с какой-то прямой, проходящей через точку O.
- Поскольку a и b параллельны, то сумма углов, которые они образуют с проходящей через точку O прямой, равна 180 градусов.
- Таким образом, в силу определения параллельных прямых, углы, образованные a и b с проходящей через точку O прямой, равны между собой.
- Таким образом, лемма о двух параллельных прямых, пересекающих плоскость, доказана.
Уравнение параллельной прямой
Общий вид уравнения
Уравнение параллельной прямой может быть записано в виде:
y = kx + b
где:
y – значение y-координаты точки на прямой
x – значение x-координаты точки на прямой
k – угловой коэффициент, определяющий наклон прямой
b – свободный член, определяющий смещение прямой по оси ординат
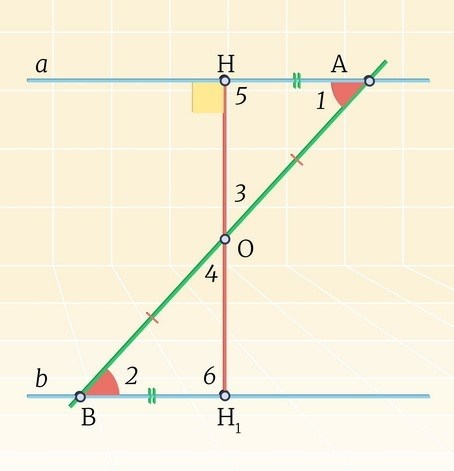
Угловой коэффициент k можно найти, используя следующую формулу:
k = tan(α)
где α – угол между параллельной прямой и положительным направлением оси абсцисс.
Примеры
Для наглядности, рассмотрим несколько примеров уравнений параллельных прямых:
- Уравнение прямой, параллельной оси абсцисс: y = b
- Уравнение прямой, параллельной оси ординат: x = a
- Уравнение прямой с угловым коэффициентом: y = kx
- Уравнение прямой с угловым коэффициентом и свободным членом: y = kx + b
Решение задачи
Для решения задачи по нахождению уравнения параллельной прямой, необходимо иметь информацию о координатах точки, через которую проходит прямая, и угловом коэффициенте.
Зная эти значения, можно подставить их в уравнение и получить уравнение параллельной прямой в плоскости.
Уравнение параллельной прямой в плоскости позволяет описать ее положение и наклон относительно осей координат. Зная координаты точки и угловой коэффициент, можно легко определить уравнение прямой.
Типы углов при параллельных прямых
При изучении теоремы о параллельных трех прямых необходимо разобраться в различных типах углов, которые образуются при такой конфигурации прямых. Вот некоторые из них:
1. Сопряженные углы
Сопряженные углы – это пары углов, которые находятся на одной стороне от пересекающихся прямых и имеют одно и то же внутреннее или внешнее положение. Сопряженные углы равны между собой и составляют при параллельных прямых. Например, если две параллельные прямые пересекаются третьей прямой, то пары сопряженных углов будут равными.
2. Вертикальные углы
Вертикальные углы – это пары углов, которые образуются при пересечении двух прямых. Они располагаются друг против друга и имеют одинаковую меру. Вертикальные углы также образуются при соответствующем пересечении попарно параллельных прямых.
3. Парные углы
Парные углы – это углы, которые являются суммой сопряженных углов. Парные углы образуются при пересечении двух попарно параллельных прямых и имеют одинаковую меру.
4. Взаимные углы
Взаимные углы – это пары углов, которые лежат на одной прямой и образуются пересечением этой прямой с другими прямыми. Взаимные углы дополняют друг друга до 180 градусов.
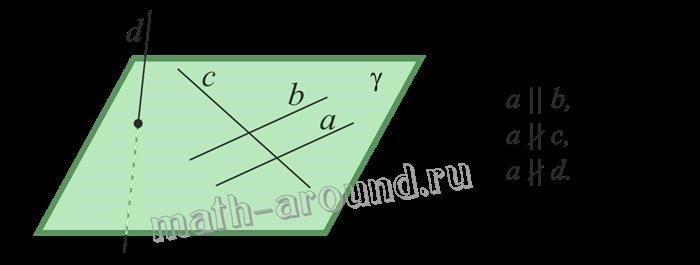
Зная эти типы углов и их свойства, мы можем более полно и глубоко изучить теорему о параллельных трех прямых и применять ее для решения задач и построения геометрических конструкций.
Теорема о параллельности трех прямых в евклидовом пространстве
Теорема о параллельности трех прямых имеет важное значение во многих областях геометрии, а также находит применение в решении различных задач. Например, она используется при рассмотрении параллельного переноса вектора и при доказательстве других геометрических утверждений.
Таким образом, теорема о параллельности трех прямых в евклидовом пространстве позволяет нам более глубоко понять и исследовать свойства прямых. Она является основой для дальнейшего изучения геометрии и находит свое применение в различных математических и физических задачах.