В логике таблица истинности – это способ представления всех возможных комбинаций значений логических переменных и результатов их сочетаний. Составление таблицы истинности помогает определить, при каких условиях выражение будет истинным или ложным. Это важный инструмент для анализа и оценки логических утверждений и выражений.
Построение таблиц истинности для сложных выражений
Построение таблиц истинности для простых выражений
Перед тем, как перейти к таблицам истинности для сложных выражений, необходимо освоить методику построения для простых выражений с использованием базовых логических операций: “И” (and), “ИЛИ” (or) и “НЕ” (not).
Для построения таблицы истинности для простого выражения нужно следовать следующим шагам:
- Определить количество переменных в выражении. Количество строк в таблице истинности будет равно 2 в степени числа переменных.
- Создать столбцы для переменных и добавить их значения в каждую строку. Варианты значений переменных могут быть “истина” (true) или “ложь” (false).
- Добавить столбец для самого выражения и вычислить его значение для каждой строки в таблице в зависимости от истинности переменных.
- Привести вычисленные значения в столбце выражения для каждой строки и получить таблицу истинности.
Например, рассмотрим простое выражение: “p И q”, где “p” и “q” – переменные.
| p | q | p И q |
|---|---|---|
| true | true | true |
| true | false | false |
| false | true | false |
| false | false | false |
Построение таблиц истинности для сложных выражений
При построении таблиц истинности для сложных выражений необходимо учитывать дополнительные логические операции, такие как “Иначе” (else) и “Иначе, если” (else if).
Для построения таблицы истинности для сложного выражения нужно следовать следующим шагам:
- Определить количество переменных в выражении. Количество строк в таблице истинности будет равно 2 в степени числа переменных.
- Создать столбцы для переменных и добавить их значения в каждую строку. Варианты значений переменных могут быть “истина” (true) или “ложь” (false).
- Добавить столбцы для каждой операции в выражении и вычислить их значения для каждой строки в таблице в зависимости от истинности переменных.
- Привести вычисленные значения в столбцах операций для каждой строки и получить таблицу истинности.
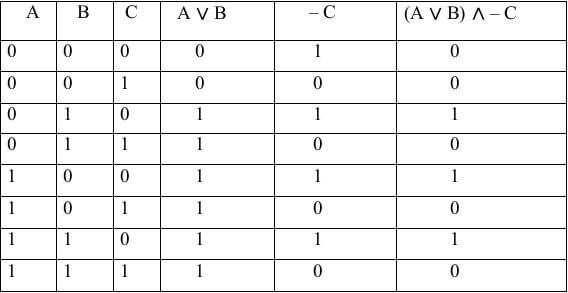
Например, рассмотрим сложное выражение: “p И q ИЛИ r”, где “p”, “q” и “r” – переменные.
| p | q | r | p И q ИЛИ r |
|---|---|---|---|
| true | true | true | true |
| true | true | false | true |
| true | false | true | true |
| true | false | false | false |
| false | true | true | true |
| false | true | false | false |
| false | false | true | true |
| false | false | false | false |
Таблицы истинности позволяют систематизировать логические выражения и проводить их анализ для принятия решений в различных областях, включая юриспруденцию, информатику, философию и другие.
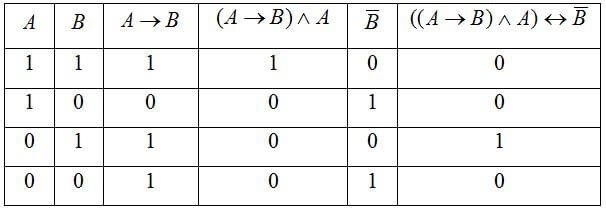
3. Равносильные логические выражения
Равносильные логические выражения могут быть представлены в виде таблиц истинности, которые демонстрируют все возможные варианты значений переменных и результаты выполнения операции.
Примеры равносильных логических выражений:
- Выражение A и B эквивалентно выражению B и A.
- Выражение A или B эквивалентно выражению B или A.
- Выражение НЕ (A и B) эквивалентно выражению (НЕ А) или (НЕ B).
- Выражение A и (B или C) эквивалентно выражению (A и B) или (A и C).
Таблица истинности для равносильных выражений:
| A | B | A и B | B и A |
|---|---|---|---|
| true | true | true | true |
| true | false | false | false |
| false | true | false | false |
| false | false | false | false |
О порядке логических операций
Типы логических операций:
- Конъюнкция (логическое И) – операция, результат которой истинен только тогда, когда оба операнда истинны, иначе результат будет ложным.
- Дизъюнкция (логическое ИЛИ) – операция, результат которой истинен, если хотя бы один из операндов истинен. Результат будет ложным только в случае, если оба операнда ложны.
- Инверсия (логическое НЕ) – операция, меняющая истинность операнда на противоположную. Если операнд истинен, то после применения инверсии он становится ложным, и наоборот.
Порядок выполнения операций:
- Сначала выполняется операция инверсии – логическое НЕ.
- Затем выполняется операция конъюнкции – логическое И.
- Последней выполняется операция дизъюнкции – логическое ИЛИ.
Например:
| Выражение | Результат |
|---|---|
| (Ложь ИЛИ Истина) ИЛИ (Истина И НЕЛЬЗЯ) | Истина |
| Ложь ИЛИ (Ложь И Истина) ИЛИ НЕТ | Ложь |
Таким образом, знание порядка логических операций позволяет проводить вычисления с учетом приоритетности операций и получать правильный результат. При необходимости можно использовать скобки, чтобы изменить порядок выполнения операций в выражении.
Порядок действий при построении таблицы истинности для логических выражений
1. Определение переменных
Прежде чем строить таблицу истинности, необходимо определить все переменные, которые присутствуют в логическом выражении. Каждая переменная обозначается буквой или словом.
2. Определение значений переменных
Для каждой переменной необходимо определить все возможные значения в соответствии с их типом. Например, логические переменные могут иметь только два значения: истина (True) или ложь (False).
3. Создание заголовков столбцов
Создайте заголовки столбцов для каждой переменной, включая логическое выражение в самом конце. Например, если у вас есть две переменные A и B, заголовки столбцов будут выглядеть так:
| A | B | Логическое выражение |
|---|
4. Заполнение значений
Заполните таблицу соответствующими значениями для каждой комбинации переменных. Начните с первой строки и пошагово меняйте значения переменных от True к False и обратно.
5. Расчет логического выражения
Примените логическое выражение к каждой комбинации значений переменных, чтобы определить его истинность или ложность. Результат запишите в столбец “Логическое выражение”. Например, если вы работаете с выражением “A И B”, результат будет True только если и A, и B равны True.
6. Интерпретация результатов
Построение таблицы истинности позволяет систематизировать информацию и облегчает анализ логических выражений. Она помогает выявить свойства истинности и ложности, а также идентифицировать возможные ошибки в логическом рассуждении. Зная правильный порядок действий, вы сможете эффективно строить таблицы истинности для любых логических выражений.
Правила построения таблицы истинности для логического выражения
Для проведения построения таблицы истинности для логического выражения следует следовать определенным правилам. Эти правила помогут jвсецг упорядочить процесс и сделают таблицу легкочитаемой и понятной.
1. Определите количество переменных
Прежде всего, необходимо определить количество переменных в логическом выражении. Каждая переменная представляет собой логический символ, который может принимать значение “Истина” или “Ложь”.
2. Определите все возможные комбинации значений переменных
На следующем шаге необходимо определить все возможные комбинации значений переменных. Если у вас есть n переменных, то количество комбинаций будет равно 2 n. Например, если у вас есть две переменные (A и B), то общее количество комбинаций значений будет равно 2 2 = 4. В данном случае это будут следующие комбинации: (Ложь, Ложь), (Ложь, Истина), (Истина, Ложь), (Истина, Истина).
3. Заполните таблицу истинности
Когда вы определили все возможные комбинации значений переменных, можно начинать заполнять таблицу истинности. Для каждой комбинации значений переменных вычисляйте значение логического выражения и записывайте его в соответствующую ячейку таблицы.
4. Подведение итога
Построение таблицы истинности позволяет наглядно увидеть все возможные комбинации значений переменных и соответствующие им значения логического выражения. Используя эту таблицу, можно проанализировать логическое выражение и определить его истинностное значение в зависимости от значений переменных.
Обратите внимание, что правила построения таблицы истинности являются алгоритмом, который может быть применен для любого логического выражения. Применение этих правил поможет вам разобраться в структуре выражения и логических связях между переменными.