Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса – линия, делящая угол треугольника пополам. Высота – отрезок, проведенный из вершины треугольника до противоположной стороны, перпендикулярно этой стороне. Эти три линии являются важными элементами треугольника и используются во многих геометрических задачах и формулах для нахождения площади и других параметров треугольника. В данной статье мы рассмотрим их свойства и применение в практике.
Подписи к слайдам:
На каждом слайде презентации необходимо предусмотреть информативные и лаконичные подписи, которые помогут читателю лучше понять и запомнить представленную информацию. Они должны быть четкими, легко читаемыми и украшать слайд, не перегружая его.
Ниже приведены некоторые примеры подписей, которые могут быть использованы в презентации:
1. Заголовки:
- Введение – слайд, представляющий общую информацию о презентации или ее цели.
- Основные понятия – слайд, содежащий определения и пояснения ключевых терминов.
- Медиана треугольника – слайд, описывающий определение и свойства медианы треугольника.
2. Пояснительные подписи:
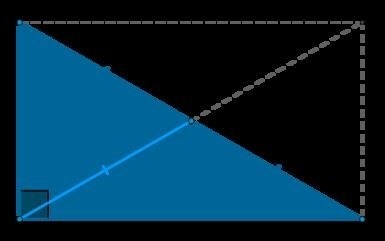
На слайде с изображением треугольника и его медиан используйте подписи, чтобы обозначить основные элементы:
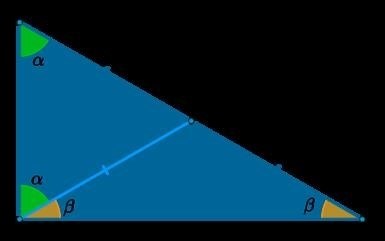
| А | Вершина треугольника |
| P | Точка пересечения медиан |
| MP | Медиана треугольника |
3. Примеры задач:
Для слайдов с решением задач можно использовать подписи, чтобы поэтапно объяснить процесс решения:
- Задача 1: Найти медиану треугольника, если известны координаты его вершин.
- Шаг 1: Найдите середину каждой стороны треугольника.
- Шаг 2: Проведите линии, соединяющие вершины треугольника с соответствующими серединами сторон.
- Шаг 3: Найдите точку пересечения этих линий – это и будет медиана треугольника.
Такие подписи помогут зрителям лучше понять каждый слайд и вместе с тем сделают презентацию более привлекательной и информативной.
Медиана, биссектриса, высота и средняя линия треугольника: основные понятия и свойства
Медиана
Медиана треугольника – это линия, соединяющая вершину треугольника с серединой противоположной стороны. Линии, которые делят стороны треугольника пополам, пересекаются в точке, называемой центром масс треугольника. Свойства медианы:
- Медиана делит треугольник на две равные по площади части.
- Точка пересечения медиан называется центром масс треугольника и делит каждую медиану в отношении 2:1.
- Медианы треугольника пересекаются в одной точке, называемой точкой Ферма.
Биссектриса
Биссектриса треугольника – это линия, которая делит угол треугольника пополам и пересекает противоположную сторону. Свойства биссектрисы:
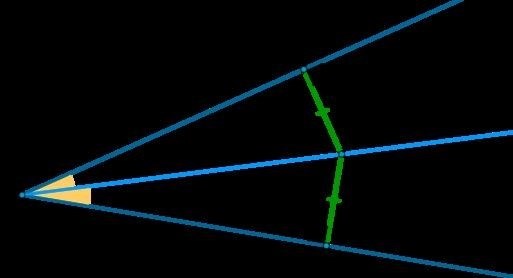
- Биссектриса делит противоположную сторону на две отрезка пропорционально смежным сторонам треугольника.
- Точка пересечения биссектрис с другими биссектрисами называется центром вписанной окружности треугольника.
- Биссектрисы треугольника пересекаются в одной точке, называемой центром вписанной окружности.
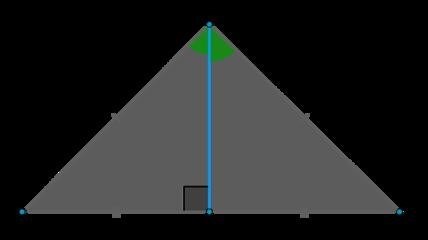
Высота
Высота треугольника – это линия, проходящая через вершину треугольника и перпендикулярная противоположной стороне. Свойства высоты:
- Высота делит треугольник на два прямоугольных треугольника.
- Точка пересечения высот треугольника называется ортоцентром.
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром.
Средняя линия
Средняя линия треугольника – это линия, соединяющая середины двух сторон треугольника. Свойства средней линии:
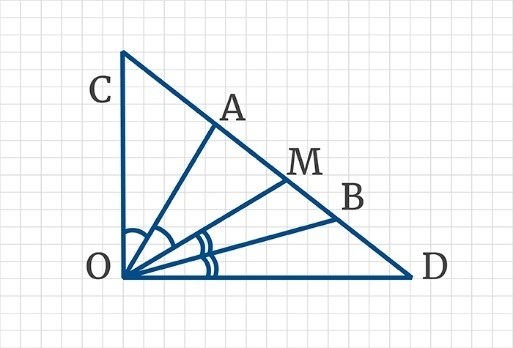
- Средняя линия параллельна третьей стороне и равна ей в половине длины.
- Три средние линии треугольника пересекаются в одной точке, называемой центром масс треугольника.
- Средняя линия делит треугольник на два равных по площади треугольника.
Медиана, биссектриса, высота и средняя линия треугольника являются важными инструментами в геометрии. Изучение их свойств и взаимосвязи помогает лучше понять строение и характеристики треугольников, а также применять их в практических задачах и решениях.
Сравнительная таблица биссектрис, медиан и высот треугольника
| Понятие | Определение | Особенности |
|---|---|---|
| Медиана | Отрезок, соединяющий вершину треугольника с серединой противоположной стороны. | Делит стороны треугольника пополам. Пересекает другие медианы в одной точке – центре тяжести треугольника. |
| Биссектриса | Отрезок, который делит угол треугольника пополам и перпендикулярен одной из его сторон. | Если биссектрисы трех углов пересекутся в одной точке, то это точка вписанной окружности треугольника. |
| Высота | Отрезок, соединяющий вершину треугольника с противоположной стороной и перпендикулярный ей. | Высоты пересекаются в одной точке, называемой ортоцентром треугольника. |
В сравнении этих трех элементов можно сказать, что каждый из них имеет свою специфику и связан с определенными особенностями треугольника. Медианы делят стороны на две равные части и пересекаются в центре тяжести, биссектрисы делят углы пополам и пересекаются в центре вписанной окружности, а высоты соединяют вершину с противоположной стороной и пересекаются в ортоцентре.
Познакомившись с этими элементами, можно более глубоко понять и изучить связи и свойства треугольника.