Корень n-ой степени – это операция, обратная возведению в n-ую степень числа. Она позволяет найти число, при возведении которого в n-ую степень получится заданное число. Корень n-ой степени имеет ряд свойств, включая свойства аддитивной и мультипликативной силы, свойства равенства и неравенства, а также свойство извлечения корня из произведения и частного.
Корень четной и нечетной степеней
Корень четной степени
Корень четной степени представляет собой операцию, обратную возведению в эту степень. Например, корень квадратный из числа является обратной операцией к возведению числа в квадрат. Если число положительное, то корень извлекается только с положительным значением.
Корень четной степени может быть представлен следующим образом:
- Корень квадратный (√x) – извлекает квадратный корень из числа x.
- Корень четвертной степени (∛x) – извлекает корень четвертой степени из числа x.
- Корень шестой степени (∜x) – извлекает корень шестой степени из числа x.
Корень нечетной степени
Корень нечетной степени также представляет собой обратную операцию возведения в эту степень. Однако, в отличие от корня четной степени, корень нечетной степени может быть извлечен из отрицательного числа. В этом случае, результат будет иметь отрицательное значение.
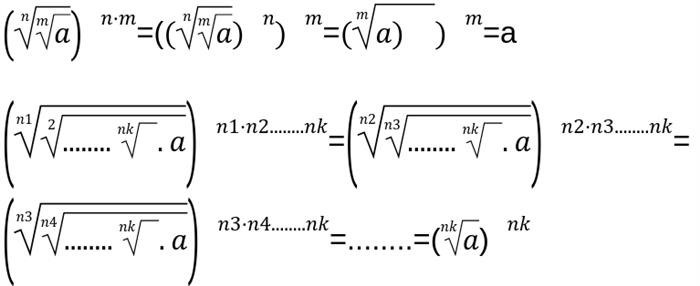
К корням нечетной степени относятся:
- Корень кубический (∛x) – извлекает кубический корень из числа x.
- Корень пятой степени (∛x) – извлекает корень пятой степени из числа x.
- Корень седьмой степени (∛x) – извлекает корень седьмой степени из числа x.
Независимо от степени числа, при извлечении корня следует помнить о следующих особенностях:
- Корень из отрицательного числа не является вещественным числом, поэтому для извлечения корня необходимо использовать комплексные числа.
- Корень из нуля равен нулю.
- Корень из единицы равен единице.
Подписи к слайдам:
Подписи к слайдам должны быть информативными и краткими. Они помогают организовать и структурировать информацию, усиливая визуальную составляющую презентации.
Зачем нужны подписи к слайдам?
1. Делают презентацию более понятной и доступной для аудитории.
2. Указывают на главные идеи, ключевые понятия и основные моменты каждого слайда.
3. Помогают сохранить последовательность и логическую связь между слайдами.
4. Облегчают запоминание информации и повышают ее усвояемость аудиторией.
Как правильно оформить подписи к слайдам?
1. Используйте краткие и информативные фразы. Не перегружайте слайды текстом.
2. Выделяйте подписи к слайдам шрифтом, размером, цветом или стилем, чтобы они были четко видны.
3. Размещайте подписи рядом с объектами, которые они описывают, чтобы аудитория могла легко соотнести текст и изображение.
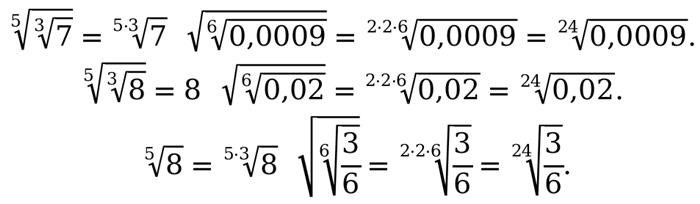
4. Используйте нумерацию слайдов с помощью подписей, чтобы помочь аудитории ориентироваться в презентации.
Примеры хорошо оформленных подписей к слайдам:
- Слайд 1: Введение в тему
- Слайд 2: Основные принципы работы
- Слайд 3: Примеры использования
Подписи к слайдам играют важную роль в организации презентации и помогают аудитории лучше понять и запомнить информацию. Они должны быть краткими, информативными и хорошо оформленными. Не забывайте об их значимости при создании презентации!
Что такое корень n-й степени из действительного числа
Корень n-й степени из действительного числа можно записать следующим образом:
√(x) = a
Где:
- √ – знак корня;
- x – исходное число;
- a – корень n-й степени из числа x.
Например, корень квадратный из числа 16 равен 4, так как 4 в квадрате равно 16.
Свойства корня n-й степени
Корень n-й степени обладает несколькими свойствами:
- Если число x положительное и n – нечётное, то корень n-й степени из числа x будет положительным.
- Если число x положительное и n – чётное, то корень n-й степени из числа x будет иметь ту же знаковую часть, что и число x.
- Если число x отрицательное, то корень чётной степени из числа x будет являться мнимым числом.
- Корень n-й степени из числа 0 равен 0. Это свойство справедливо для любого n.
Примеры вычисления корня n-й степени
1. Вычислим корень кубический из числа 27.
√(27) = 3
2. Найдём корень квадратный из числа -9.
√(-9) = √(-1) * √(9) = i * 3 = 3i
Где i – мнимая единица.
3. Рассчитаем корень пятой степени из числа 32.
√(32) = 2
4. Посчитаем корень четвёртой степени из числа 16.
√(16) = 4
Таким образом, корень n-й степени из действительного числа позволяет найти число, при возведении которого в степень n получается исходное число.
Свойства арифметического квадратного корня
1. Определение корня
Арифметический квадратный корень из числа a – это такое неотрицательное число x, что x*x = a. Обозначение: sqrt(a).
2. Существование корня
- Для любого положительного числа a существует единственное арифметическое квадратное корень.
- Для отрицательного числа арифметический квадратный корень не существует в области действительных чисел.
3. Свойства арифметического квадратного корня
Для любых положительных чисел a и b, и любого неотрицательного целого числа n, справедливы следующие свойства:
| Свойство | Пример |
|---|---|
| Сложение корней | sqrt(a) + sqrt(b) = sqrt(a+b) |
| Вычитание корней | sqrt(a) – sqrt(b) = sqrt(a-b) |
| Умножение корней | sqrt(a) * sqrt(b) = sqrt(a*b) |
| Деление корней | sqrt(a) / sqrt(b) = sqrt(a/b) |
4. Сокращение корней
- Если a и b являются полными квадратами, то можно применить свойство сокращения корней:
sqrt(a) * sqrt(b) = sqrt(a*b)
Например, чтобы сократить корень из произведения чисел 9 и 4, мы можем записать это как:
sqrt(9) * sqrt(4) = sqrt(36) = 6
Логарифмическая функция. Свойства и график функции
Основное свойство логарифмической функции:
- Логарифм от произведения двух чисел равен сумме логарифмов от этих чисел;
- Логарифм от частного двух чисел равен разности логарифмов от этих чисел;
- Логарифм от числа, возведенного в степень, равен произведению степени и логарифма от числа;
- Логарифм от единицы по любому основанию равен нулю;
- Логарифм от числа по тому же основанию, равному основанию логарифма, равен единице.
График логарифмической функции:
График логарифмической функции имеет своеобразную форму, которая зависит от основания логарифма. Например, для функции с основанием 10, график проходит через точку (1, 0), а затем скорее всего возрастает медленно или убывает медленно. Однако форма графика может меняться в зависимости от основания логарифма и других параметров функции.
| Число | Логарифм |
|---|---|
| 1 | 0 |
| 10 | 1 |
| 100 | 2 |
| 1000 | 3 |
Логарифмическая функция широко применяется в математике, физике, экономике и других науках, где она помогает в решении задач, связанных с процентными изменениями, сложными зависимостями и экспоненциальным ростом.
Калькулятор квадратных корней
Для использования калькулятора квадратных корней достаточно ввести число, из которого нужно извлечь корень, и нажать на кнопку “Вычислить”. Калькулятор автоматически выведет результат на экран.
Использование калькулятора квадратных корней упрощает процесс вычисления корней и позволяет быстро получать результаты. Он может быть полезен при решении математических задач, таких как вычисление длины стороны квадрата или нахождение среднего значения.
Важно помнить, что квадратный корень из отрицательного числа является мнимым числом. В данном случае калькулятор может вывести результат в виде комплексного числа.
Итак, калькулятор квадратных корней представляет собой удобный инструмент для вычисления корней чисел. Он позволяет быстро и точно определить значение квадратного корня и может быть полезен в различных математических задачах.