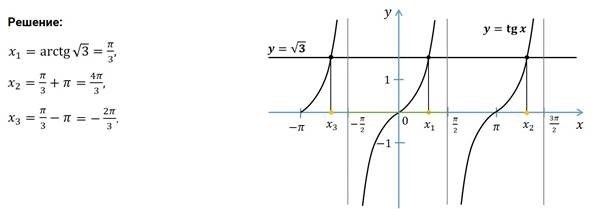
Тангенс – это основная тригонометрическая функция, которая используется для описания отношения противоположной и прилежащей стороны прямоугольного треугольника. Функция y = tg x имеет ряд свойств, включая ограниченность, периодичность, стремление к бесконечности и симметрию относительно точки (frac{pi}{2}).
Выражения через гиперболические функции
Гиперболические функции
Гиперболические функции определяются с помощью экспоненты и обратной функции экспоненты. Они могут быть выражены через другие гиперболические функции и тригонометрические функции. Некоторые из наиболее распространенных гиперболических функций:
- Гиперболический синус (sinh x)
- Гиперболический косинус (cosh x)
- Гиперболический тангенс (tanh x)
Выражения через гиперболические функции
Выражения, содержащие гиперболические функции, могут быть приведены к более простым формам с использованием связей между гиперболическими функциями и тригонометрическими функциями.
Например, гиперболический синус может быть выражен через гиперболический косинус и наоборот:
sinh x = (exp(x) – exp(-x)) / 2
cosh x = (exp(x) + exp(-x)) / 2
Также, гиперболический тангенс может быть выражен через гиперболический синус и косинус:
tanh x = sinh x / cosh x
Примеры выражений
С использованием этих выражений, можно решать различные математические задачи. Например, выражение 2sinh 2x + 3cosh 2x может быть приведено к более простой форме:
2sinh 2x + 3cosh 2x = 2((exp(x) - exp(-x)) / 2) 2 + 3((exp(x) + exp(-x)) / 2) 2= 2(exp 2(x) - 2exp(x)exp(-x) + exp (-2x)) + 3(exp 2(x) + 2exp(x)exp(-x) + exp (-2x))= 2exp 2(x) - 4 + 2exp (-2x) + 3exp 2(x) + 6 + 3exp (-2x)= 5exp 2(x) + 5exp (-2x) + 2Таким образом, выражение 2sinh 2x + 3cosh 2x может быть упрощено до 5exp 2(x) + 5exp (-2x) + 2.
Использование гиперболических функций в приложениях
Гиперболические функции имеют множество применений в физике, инженерии и других науках. Они используются, например, при решении уравнений теплопроводности, колебательных систем и электромагнитного поля.
Знание выражений через гиперболические функции и их свойств может быть полезно при анализе данных, построении моделей и решении различных задач в научной и инженерной областях.

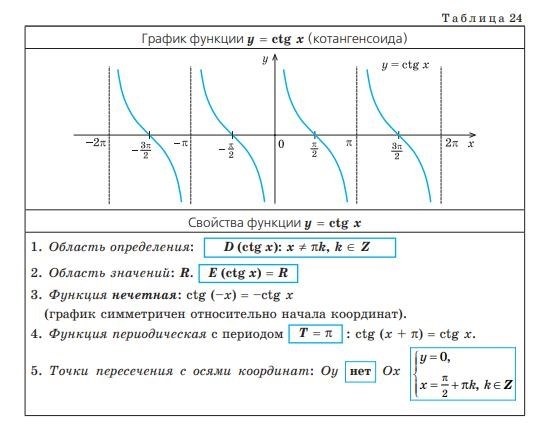
Свойства тангенса и котангенса
Свойства тангенса:
- Ограничение области определения: тангенс определен для всех вещественных чисел, кроме углов, при которых синус равен нулю.
- Периодичность: тангенс имеет период равный π (пи), то есть tg(x) = tg(x + kπ), где k – любое целое число.
- Четность: тангенс является нечетной функцией, что означает, что tg(-x) = -tg(x).
- Тангенс угла: тангенс угла равен отношению синуса угла к косинусу угла, т.е. tg(x) = sin(x) / cos(x).
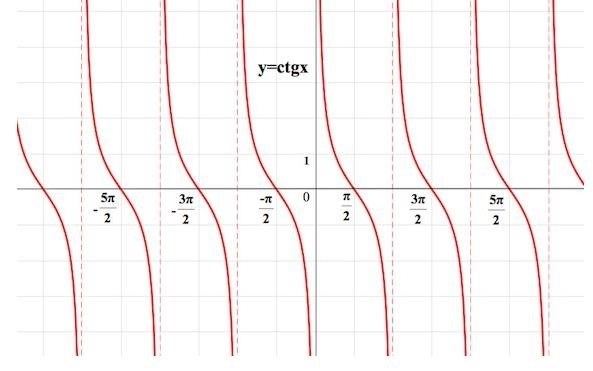
Свойства котангенса:
- Ограничение области определения: котангенс определен для всех вещественных чисел, кроме углов, при которых косинус равен нулю.
- Периодичность: котангенс имеет период равный π (пи), то есть ctg(x) = ctg(x + kπ), где k – любое целое число.
- Четность: котангенс является нечетной функцией, что означает, что ctg(-x) = -ctg(x).
- Котангенс угла: котангенс угла равен отношению косинуса угла к синусу угла, т.е. ctg(x) = cos(x) / sin(x).
Тангенс и котангенс в прямоугольном треугольнике:
В прямоугольном треугольнике тангенс угла α можно определить как отношение противолежащего катета (стороны) к прилежащему катету,
а котангенс – как отношение прилежащего катета к противолежащему катету. Таким образом, tg(α) = a / b и ctg(α) = b / a, где a и b –
длины катетов треугольника.
Соотношение между котангенсом и тангенсом:
Соотношение между котангенсом и тангенсом выражается следующей формулой:
ctg(x) = 1 / tg(x), где x – угол, для которого определены функции.
| Угол (x) | Тангенс (tg(x)) | Котангенс (ctg(x)) |
|---|---|---|
| 0 | 0 | ∞ |
| π/4 | 1 | 1 |
| π/6 | √3/3 | √3 |
| π/3 | √3 | √3/3 |
| π/2 | ∞ | 0 |
Приложения тангенса и котангенса:
Тангенс и котангенс применяются в различных областях знаний. Например, в геометрии они используются для решения задач
на нахождение противоположного катета по известным значениям угла и прилежащего катета в прямоугольном треугольнике. В
физике и инженерии они применяются при решении задач на определение сил и направления векторов.
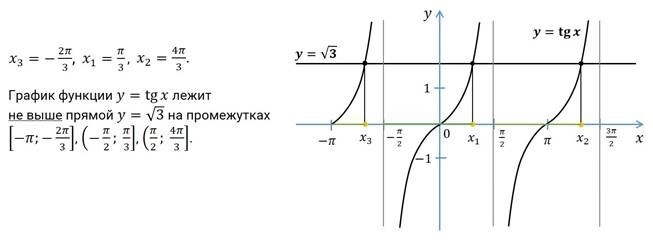
Таблица тангенсов и котангенсов
Тангенс
Тангенс угла, обозначаемый как tg x или tan x, определяется отношением противоположного катета к прилежащему катету в прямоугольном треугольнике.
Таблица тангенсов предоставляет значения тангенсов для различных углов от 0° до 90°. Ниже приведены некоторые из этих значений:
| Угол (градусы) | Тангенс |
|---|---|
| 0° | 0 |
| 30° | √3 / 3 |
| 45° | 1 |
| 60° | √3 |
| 90° | Не определено |
Тангенс угла 90° не определен, так как противоположный катет становится бесконечно большим, а прилежащий катет равен нулю.
Котангенс
Котангенс угла, обозначаемый как cot x или ctg x, определяется отношением прилежащего катета к противоположному катету в прямоугольном треугольнике.
Таблица котангенсов предоставляет значения котангенсов для различных углов от 0° до 90°. Ниже приведены некоторые из этих значений:
| Угол (градусы) | Котангенс |
|---|---|
| 0° | Не определено |
| 30° | √3 |
| 45° | 1 |
| 60° | √3 / 3 |
| 90° | 0 |
Котангенс угла 0° не определен, так как прилежащий катет равен нулю, а противоположный катет становится бесконечно большим.
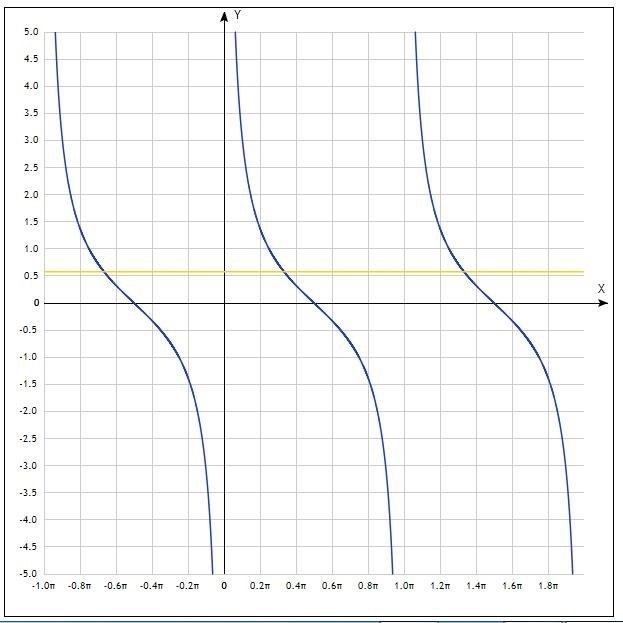
Свойства функции $f(x)=tan{x}$
Функция $f(x)=tan{x}$, где $x$ принадлежит диапазону действительных чисел, имеет ряд важных свойств. Рассмотрим их подробнее:
1. Определение и область значений
Функция тангенс определена как отношение синуса и косинуса угла: $f(x)=frac{{sin{x}}}{{cos{x}}}$. Она имеет периодичность $pi$ и область значений от минус бесконечности до плюс бесконечности.
2. Нули и полюса
Уравнение $tan{x}=0$ имеет решения при $x=kpi$, где $k$ – целое число. То есть, нули функции $tan{x}$ находятся в точках, где значение синуса равно нулю.
Функция $tan{x}$ также имеет полюса в точках, где $cos{x}=0$. Такие точки называются асимптотами функции.
3. Симметричность и периодичность
Функция $tan{x}$ обладает несколькими важными свойствами симметрии и периодичности:
- Симметрична относительно начала координат: $f(-x)=-f(x)$.
- Периодична с периодом $pi$: $f(x+pi)=f(x)$.
- Симметрична относительно вертикальной прямой $x=frac{pi}{2}$: $f(frac{pi}{2}-x)=-frac{1}{f(x)}$.
4. Рост и убывание
На интервалах между асимптотами функция $tan{x}$ растет и убывает:
- На каждом отрезке длиной $pi$ функция либо возрастает, либо убывает.
- Максимумы и минимумы функции на этих отрезках лежат в точках $frac{pi}{2}+kpi$, где $k$ – целое число.
Все результаты и свойства, описанные выше, основаны на математических доказательствах и являются важными для понимания поведения функции $tan{x}$.
Разложения в ряды
Разложение в ряды позволяет аппроксимировать функцию с неограниченным числом слагаемых. Он может быть полезным для анализа функций, которые сложно или невозможно представить в виде аналитической формулы.
Методы разложения в ряды
- Разложение в ряды Тейлора;
- Разложение в ряды Фурье;
- Разложение в ряды Лорана;
- Разложение в ряды Чебышева.
Разложение в ряд Тейлора
Разложение в ряд Тейлора – это разложение функции в бесконечную сумму степеней переменной. Ряд Тейлора используется для аппроксимации функции в окрестности точки, в которой происходит разложение.
Ряд Тейлора может быть полезен для вычисления значений функции вблизи точки, а также для нахождения производных функции и аппроксимации интегралов.
Разложение в ряд Фурье
Разложение в ряд Фурье – это представление функции в виде бесконечной суммы гармонических функций (синусов и косинусов). Ряд Фурье позволяет аппроксимировать функцию с периодическим повторением.
Ряд Фурье имеет широкое применение в теории сигналов, обработке изображений, анализе сигналов со сложной формой и многих других областях.
Разложение в ряд Лорана
Разложение в ряд Лорана – это разложение функции в бесконечную сумму степеней переменной, включающую как положительные, так и отрицательные степени. Разложение в ряд Лорана используется для анализа функций с особенностями, такими как полюса и существенные особые точки.
Разложение в ряд Лорана позволяет аппроксимировать функцию как в окрестности полюса, так и вне его.
Разложение в ряд Чебышева
Разложение в ряд Чебышева – это разложение функции в ряд, состоящий из полиномов Чебышева, которые являются ортогональными на заданном интервале. Ряд Чебышева позволяет аппроксимировать функции на заданном интервале с высокой точностью.
Разложение в ряд Чебышева может быть полезным для вычисления значений функции и аппроксимации функций с большим числом слагаемых.
График функции $y=tgx$
Функция $y=tgx$ описывает зависимость значения тангенса от значения аргумента. График функции представляет собой кривую, которая проходит через точку $(0,0)$ и имеет период равный $pi$.
Основные свойства графика функции $y=tgx$:
- Периодичность: график функции повторяется через каждый период $pi$, то есть при добавлении или вычитании $pi$ в аргументе, значение тангенса не меняется.
- Асимптоты: график функции имеет вертикальные асимптоты в точках $x=(2k+1)frac{pi}{2}$, где $k$ – любое целое число. Они представляют собой прямые, которые график функции приближается, но никогда не пересекает.
- Пересечение с осью абсцисс: график функции пересекает ось абсцисс в точках $x=kpi$, где $k$ – любое целое число.
График функции $y=tgx$ можно представить в виде таблицы:
| $x$ | $tgx$ |
|---|---|
| $0$ | $0$ |
| $frac{pi}{4}$ | $1$ |
| $frac{pi}{2}$ | $infty$ |
| $frac{3pi}{4}$ | $-1$ |
| $pi$ | $0$ |
График функции $y=tgx$ удобно использовать для решения различных задач, связанных с тригонометрией и геометрией. Он помогает найти значения тангенса в определенных точках и анализировать свойства функции.
Выражения через комплексные числа
В статье мы рассмотрели свойства функции y = tg x, изучили ее график, а также основные характеристики этой функции. В процессе исследования мы обнаружили, что функция y = tg x обладает множеством интересных свойств и приложений.
Теперь рассмотрим выражения через комплексные числа. Комплексные числа включают в себя действительную и мнимую части, обозначаемые как a и b соответственно. Одно из основных свойств комплексных чисел – возможность представления их в показательной форме:
z = a + bi = r(cos θ + i sin θ)
где z – комплексное число, a и b – его действительная и мнимая части, r – модуль числа z, θ – аргумент числа z.
Комплексные числа позволяют нам решать уравнения, которые не имели решений в области действительных чисел. Они также находят применение в физике, инженерии и других областях науки и техники.
Итак, выражения через комплексные числа позволяют нам работать с объектами, которые не имеют простого представления в виде действительных чисел. Они открывают новые возможности для анализа и решения различных задач. Комплексные числа являются важным инструментом в математике и вычислительной технике, и их изучение полезно для понимания и использования более сложных концепций и задач.