Степенная функция – это функция вида f(x) = kx n, где k и n – постоянные числа, а x – переменная. От значения показателя n зависит форма графика функции. Если n > 0, то график функции имеет вид возрастающей или убывающей кривой, в зависимости от знака коэффициента k. Если n = 0, то график функции представляет собой прямую горизонтальную прямую. Если n < 0, то график функции имеет вид убывающей или возрастающей кривой, в зависимости от знака коэффициента k.
Формулы со степенной функцией
1. Функция мощности
Степенная функция может использоваться для описания отношений между двумя переменными, где одна переменная зависит от другой в степенной форме. Например, функция мощности может быть записана в виде y = kx n, где y – зависимая переменная (величина, которую нам нужно найти), x – независимая переменная (изменяющаяся величина) и n – показатель степени (степень, в которую возводится x).
2. Формулы преобразования степеней
Существуют несколько формул, которые позволяют преобразовывать степени и упрощать выражения со степенями. Некоторые из них:
- Умножение степеней с одинаковым основанием: x m * x n = x (m + n)
- Деление степеней с одинаковым основанием: x m / x n = x (m – n)
- Возведение степени в степень: (x m) n = x (m * n)
- Умножение степени на число: (x m) n = (x (m * n)) k
3. Формулы с отрицательными степенями
Если показатель степени n отрицателен, то степенная функция может быть записана в виде y = k/x m, где m = -n. Например, если у нас есть функция y = 1/x 2, то она описывает обратно пропорциональную зависимость между переменными y и x.
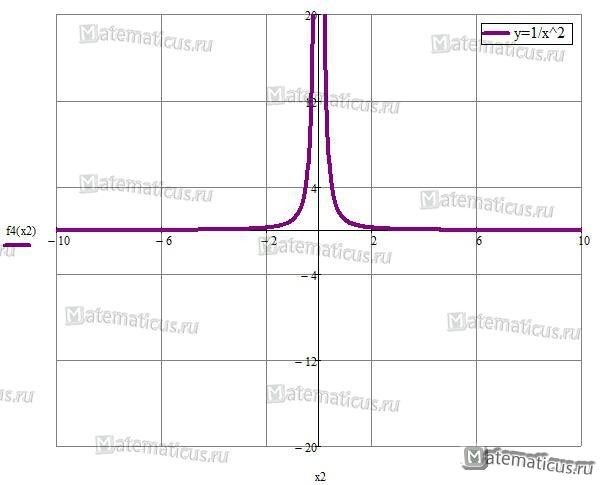
4. Логарифмическая функция
Логарифмическая функция является обратной функцией к степенной функции. Ее общий вид можно представить в виде y = logx(k), где x – основание логарифма, k – значение функции. Например, функция y = log2(8) описывает, в какую степень нужно возвести основание 2, чтобы получить 8.
5. График степенной функции
График степенной функции может иметь различные формы в зависимости от значений показателя степени n и коэффициента k. Например, если n > 1, график будет иметь форму возрастающей экспоненты, а если 0 < n < 1, график будет иметь форму убывающей экспоненты. Также график будет проходить через точку (0, k), если n > 0.
Виды и свойства степенных функций
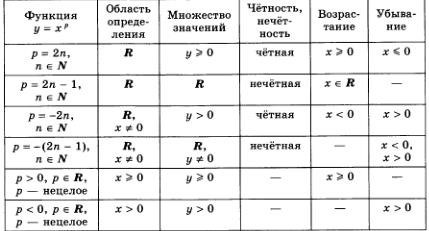
Виды степенных функций:
- Линейная функция (b = 1)
- Квадратичная функция (b = 2)
- Кубическая функция (b = 3)
- Обратная степенная функция (b = -1)
- Корневая функция (0 < b < 1)
Свойства степенных функций:
1. Знак коэффициента ‘a’ определяет направление графика функции.
- Если а > 0, график функции имеет возрастающий характер.
- Если а < 0, график функции имеет убывающий характер.
2. Показатель ‘b’ определяет форму графика функции.
- При b > 1, график функции стремится к бесконечности при x > 0 и x < 0.
- При 0 < b < 1, график функции стремится к нулю при x > 0 и x < 0.
3. Область определения степенной функции зависит от показателя ‘b’.
- Если b – целое число или дробное число с нечетным знаменателем, то область определения функции – множество всех действительных чисел.
- Если b – дробное число с четным знаменателем, то область определения функции – все положительные числа и ноль.
4. Степенная функция может иметь асимптоту графика при x = 0.
- Если b > 0, то график функции имеет горизонтальную асимптоту при y = 0.
- Если b < 0, то график функции имеет вертикальную асимптоту.
Примеры степенных функций:
| Функция | График |
|---|---|
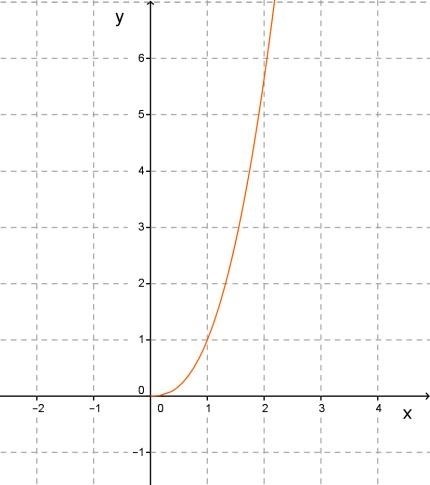
| y = 2x |  |
| y = x 2 |  |
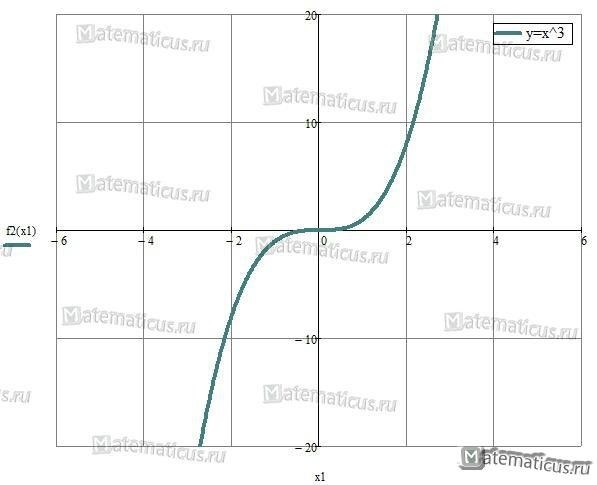
| y = x 3 |  |
Степенные функции широко применяются в математике и естественных науках для моделирования различных процессов и явлений. Они обладают множеством интересных свойств, которые позволяют исследовать их поведение и использовать в различных практических задачах.
Как строить графики степенных функций
Для построения графиков степенных функций необходимо учитывать их основные свойства и принципы. Вот несколько шагов, которые помогут вам построить правильный график:
- Определите показатель степени (степень функции): определите, является ли число в показателе степени положительным или отрицательным. Это позволит понять, как будет меняться график.
- Определите значения функции при некоторых значениях аргумента: выберите несколько значений для аргумента функции и рассчитайте соответствующие значения функции. Это поможет вам построить несколько точек на графике.
- Постройте график, используя найденные точки: используйте найденные значения для построения точек на графике. Если показатель степени положительный, график будет идти вверх или вниз в зависимости от значения показателя. Если показатель степени отрицательный, график будет идти влево или вправо.
- Учитывайте особенности функции: степенные функции могут иметь различные особенности, такие как асимптоты, точки перегиба и экстремумы. Учитывайте эти особенности при построении графика.
Важно понимать, что процесс построения графиков степенных функций может быть сложным и требует практики. Однако, знание основных принципов и свойств степенных функций поможет вам справиться с этой задачей.