Дроби являются важным элементом в математике, и иногда может возникнуть необходимость найти их дополнительные множители. Дополнительный множитель – это такое число, которое нужно умножить на дробь, чтобы получить целое число или дробь с удобным знаменателем. В данной статье будут рассмотрены способы нахождения дополнительного множителя для облегчения работы с дробями.
Сложение смешанных чисел
Для сложения смешанных чисел необходимо следовать определенным шагам:
- Сложение целых частей чисел. Целые части складываются обычным образом.
- Сложение десятичных частей чисел. Десятичные части также складываются обычным образом, при этом десятки, сотни и т.д. дополняются нулями при необходимости.
- Сокращение полученной суммы. Если дополнительный множитель есть, он может быть применен для сокращения суммы с учетом общего знаменателя.
Процесс сложения смешанных чисел может быть представлен в виде таблицы:
| Целая часть | Десятичная часть | Сумма чисел |
|---|---|---|
| 5 | 0.3 | 5.3 |
| 2 | 0.7 | 2.7 |
| Сумма | 8 |
В приведенном примере были сложены два смешанных числа: 5 0.3 и 2 0.7. В результате сложения получилось число 8 0, что является суммой целых и десятичных частей.
Сложение смешанных чисел может использоваться в различных сферах жизни. Например, при расчете времени, объединении дробных величин или при выполнении финансовых операций. Понимание процесса сложения смешанных чисел дает возможность точно решать задачи и получать верные результаты.
Понятие дополнительного множителя
Как найти дополнительный множитель:
- Разложите числитель и знаменатель на простые множители.
- Найдите общие множители числителя и знаменателя.
- Поделите общие множители на результат деления числителя и знаменателя на их НОД (наибольший общий делитель).
- Умножьте числитель и знаменатель на полученные дополнительные множители.
Пример:
| Исходная дробь | Разложение на простые множители | Общие множители | Дополнительные множители | Упрощенная дробь |
|---|---|---|---|---|
| 12/18 | 2 * 2 * 3 / 2 * 3 * 3 | 2, 3 | 1, 1 | 12/18 |
| 15/25 | 3 * 5 / 5 * 5 | 5 | 1 | 15/25 |
В приведенных примерах дополнительные множители равны единице, что означает, что исходные дроби уже упрощены и не требуют дополнительного умножения.
Понимание понятия дополнительного множителя позволяет более эффективно упрощать дроби и находить общие черты между ними. Это полезное знание в математике и может быть применено при решении задач по работы с дробями.

Напоминание о числовых дробях: Сложение, Вычитание, Сравнение.
Сложение числовых дробей
При сложении числовых дробей необходимо иметь общий знаменатель. Если у дробей уже есть общий знаменатель, то сложение сводится к сложению числителей. Если знаменатели разные, нужно привести дроби к общему знаменателю путем умножения числителя и знаменателя каждой дроби на такое число, чтобы знаменатели стали равными.
Пример:
- 1/4 + 1/3 = (1*3)/(4*3) + (1*4)/(3*4) = 3/12 + 4/12 = 7/12
- 2/5 + 3/7 = (2*7)/(5*7) + (3*5)/(7*5) = 14/35 + 15/35 = 29/35
Вычитание числовых дробей
При вычитании числовых дробей также необходимо иметь общий знаменатель. Если у дробей уже есть общий знаменатель, вычитание сводится к вычитанию числителей. Если знаменатели разные, нужно привести дроби к общему знаменателю, а затем вычесть числители.
Пример:

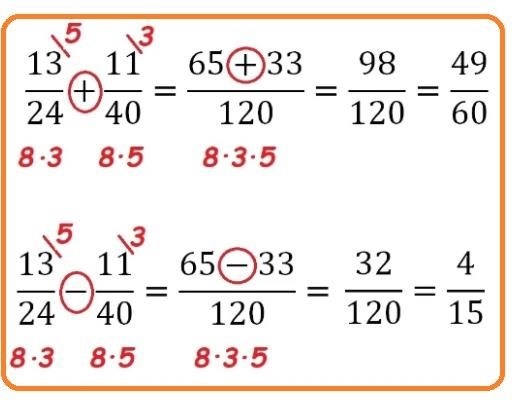
- 3/4 – 2/5 = (3*5)/(4*5) – (2*4)/(5*4) = 15/20 – 8/20 = 7/20
- 5/6 – 1/3 = (5*3)/(6*3) – (1*6)/(3*6) = 15/18 – 6/18 = 9/18 = 1/2
Сравнение числовых дробей
При сравнении двух числовых дробей необходимо сравнивать их числители и знаменатели. Если числитель одной дроби больше числителя другой дроби, а знаменатель одной дроби меньше знаменателя другой дроби, то первая дробь больше второй. Если числитель одной дроби меньше числителя другой дроби, а знаменатель одной дроби больше знаменателя другой дроби, то первая дробь меньше второй. Если числители или знаменатели равны, то дроби равны.
Пример:
- 1/3 > 1/4, так как 1 > 3/4
- 2/5 < 3/5, так как 2 < 3
- 3/6 = 1/2, так как числители и знаменатели равны
Теперь, после воспоминания о сложении, вычитании и сравнении числовых дробей, вы готовы использовать эти навыки для решения различных задач в области математики и не только.
Как привести дроби к общему знаменателю: алгоритм
Когда вам необходимо сложить или вычесть дроби с разными знаменателями, для удобства расчетов используется приведение дробей к общему знаменателю. Алгоритм приведения дробей к общему знаменателю включает следующие шаги:
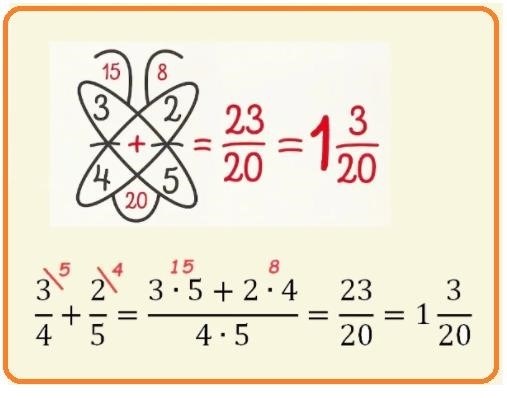
- Найдите наименьшее общее кратное (НОК) знаменателей дробей. Для этого вы можете использовать различные методы: наименьший общий множитель, разложение на простые множители или таблицу умножения.
- Умножьте каждую дробь на такое число, чтобы ее знаменатель стал равным НОК. При этом числитель дроби остается неизменным.
- Пересчитайте полученные дроби. Если требуется, выполните операции сложения или вычитания дробей с одинаковыми знаменателями.
- Приведите полученную дробь к несократимому виду. Для этого можно сократить числитель и знаменатель на их наибольший общий делитель (НОД).
Приведение дробей к общему знаменателю упрощает выполнение арифметических операций с дробями и позволяет получить более точный результат. Помните, что при выполнении алгоритма важно не потерять точность дробей и учитывать возможность появления дополнительных множителей. Следуя этому алгоритму, вы сможете успешно привести дроби к общему знаменателю и провести необходимые арифметические действия со схожими дробями.