Сложение и вычитание дробей с разными знаменателями является одной из основных операций в математике. При выполнении этих операций необходимо найти общий знаменатель для дробей и затем привести их к общему знаменателю. Для этого можно использовать методы приведения дробей к общему знаменателю или методы несократимых дробей.
Что делать, если у дроби есть целая часть
При сложении и вычитании дробей с разными знаменателями часто возникает ситуация, когда в одной из дробей есть целая часть. Чтобы правильно выполнять такие операции, нужно уметь работать с дробями, включая целую часть. В этой статье мы рассмотрим, что делать, если у дроби есть целая часть.
1. Переведите целую часть в десятичную дробь
Если у дроби есть целая часть, то ее можно перевести в десятичную дробь, чтобы проводить операции сложения или вычитания. Для этого достаточно записать целую часть дроби перед знаком запятой.
2. Действуйте с десятичными дробями, как с обычными
После перевода целой части в десятичную дробь, вы можете выполнять операции сложения и вычитания, как обычно. Складывайте или вычитайте числители и знаменатели дробей, при этом учитывайте знаки операций.
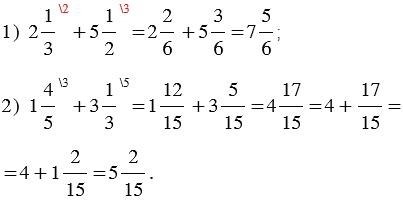
3. Верните результат в виде смешанной дроби или обыкновенной дроби
После выполнения операции сложения или вычитания, результат можно привести к виду смешанной дроби (дробь, у которой целая часть записана отдельно от дробной) или обыкновенной дроби (дробь, в которой только числитель и знаменатель).
Если в результате операции получается целое число без дробной части, то его можно записать в виде смешанной дроби, где целая часть стоит перед дробной и отделяется запятой.
Если в результате операции получается дробное число, то его можно записать в виде обыкновенной дроби, где числитель – это число после запятой, а знаменатель – единица со столько нулей, сколько цифр после запятой.
Примеры:
1. Если у нас есть дробь 3 1/4, то мы можем перевести ее в десятичную дробь следующим образом: 3 + 1/4 = 3.25. После этого мы можем провести операции сложения и вычитания с этой десятичной дробью.

2. Если у нас есть дроби 2 3/5 и 1 1/2, то мы можем перевести их в десятичные дроби: 2 + 3/5 = 2.6, 1 + 1/2 = 1.5. Затем мы можем провести операцию сложения десятичных дробей: 2.6 + 1.5 = 4.1. И, наконец, мы можем вернуть результат в виде смешанной дроби: 4.1 = 4 1/10.
Итоги
Если у дроби есть целая часть, то ее можно перевести в десятичную дробь и проводить операции сложения и вычитания, как с обычными дробями. После операции можно вернуть результат в виде смешанной или обыкновенной дроби, в зависимости от того, является ли результат целым числом или дробным.
Приведение алгебраических дробей к общему знаменателю
Алгоритм приведения дробей к общему знаменателю:
- Найдите наименьшее общее кратное (НОК) знаменателей дробей.
- Умножьте каждую дробь на такое число, чтобы ее знаменатель стал равен НОК.
- После этого дроби будут иметь одинаковые знаменатели, и вы сможете складывать или вычитать их.
Пример:
Даны две дроби: 2/3 и 3/4.
Найдем НОК знаменателей:

- Знаменатель дроби 2/3 равен 3.
- Знаменатель дроби 3/4 равен 4.
Наименьшее общее кратное для чисел 3 и 4 равно 12.
Умножим каждую дробь на такое число, чтобы знаменатель стал равен 12:
- 2/3 * 4/4 = 8/12
- 3/4 * 3/3 = 9/12
Теперь дроби имеют общий знаменатель 12, и мы можем их складывать или вычитать:
- 8/12 + 9/12 = 17/12
- 8/12 – 9/12 = -1/12
Приведение алгебраических дробей к общему знаменателю позволяет выполнять операции сложения и вычитания с дробями, имеющими разные знаменатели. Этот алгоритм основан на нахождении наименьшего общего кратного знаменателей и умножении каждой дроби на подходящий коэффициент. Использование общего знаменателя позволяет сравнивать и складывать дроби, делая математические вычисления более удобными и точными.

Резюме: общая схема вычислений
В данном резюме представлена общая схема вычислений, которая включает в себя несколько основных этапов.
1. Определение задачи
Первым шагом в процессе вычислений является четкое определение задачи. Необходимо понять, что именно требуется посчитать и какие данные будут использованы.
2. Сбор данных
Для выполнения вычислений необходимо собрать все необходимые данные. Это может включать в себя числовые значения, формулы, таблицы, графики и другую информацию.
3. Выбор метода вычислений
На третьем этапе следует выбрать подходящий метод вычислений, который будет использоваться для решения поставленной задачи. Это может быть метод аналитического решения, численных методов или комбинация различных подходов.

4. Выполнение вычислений
После выбора метода вычислений следует выполнить сам расчет. Необходимо следовать выбранной методике и использовать соответствующие формулы, уравнения и алгоритмы для получения результатов.
5. Проверка результатов
После выполнения вычислений необходимо проверить полученные результаты на корректность. Это может включать в себя сравнение с известными данными, анализ результатов на соответствие ожиданиям и другие методы контроля.
6. Интерпретация результатов
Что делать, если знаменатели разные?
Когда мы работаем с дробями, часто сталкиваемся с ситуацией, когда знаменатели дробей разные. В таком случае, прежде чем складывать или вычитать дроби, необходимо привести их к общему знаменателю.
Существует несколько способов приведения дробей к общему знаменателю:

- Найти наименьшее общее кратное (НОК) знаменателей и заменить каждый знаменатель на НОК.
- Умножить каждую дробь на такое число, чтобы знаменатель стал равным НОК.
После приведения дробей к общему знаменателю, мы можем выполнять операции сложения и вычитания стандартным образом.
Итак, чтобы сложить или вычесть дроби с разными знаменателями, мы должны сначала привести их к общему знаменателю. После этого мы можем выполнять операции сложения или вычитания числителей дробей и сохранить общий знаменатель.
Знание правил сложения и вычитания дробей с разными знаменателями позволит нам более гибко и точно решать математические задачи, связанные с этой операцией. Важно не забывать о приведении к общему знаменателю, чтобы получить правильный результат.