Метод Крамера – один из способов решения систем линейных уравнений с помощью определителей матриц. Он основан на использовании соотношения между определителями и решениями системы. Метод позволяет найти значения неизвестных переменных системы, если определитель основной матрицы не равен нулю. Для этого необходимо поочередно заменить столбец свободных членов в исходной системе на столбцы коэффициентов переменных и вычислить определители. После нахождения значений определителей, полученные значения используются для вычисления искомых переменных. Метод Крамера является вычислительно сложным, но позволяет получить точное решение системы в некоторых случаях.
2. Обратная матрица
2.1. Критерии существования обратной матрицы
Для того чтобы обратная матрица существовала, необходимо и достаточно, чтобы матрица системы линейных уравнений была невырожденной. Это означает, что ее определитель должен быть отличен от нуля.
Если определитель матрицы равен нулю, то обратная матрица не существует. В этом случае система линейных уравнений может иметь либо бесконечное число решений, либо не иметь их вовсе.
2.2. Поиск обратной матрицы
Для того чтобы найти обратную матрицу, необходимо выполнить ряд математических операций.
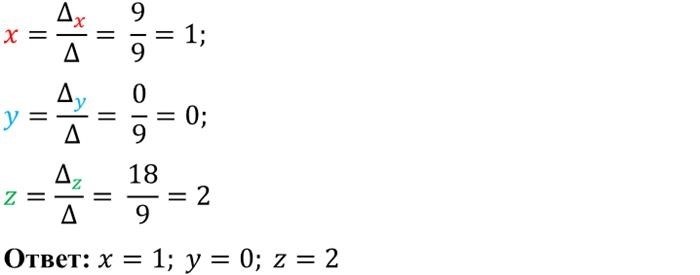
- Вычислить определитель матрицы системы линейных уравнений. Если определитель равен нулю, обратной матрицы не существует.
- Вычислить миноры матрицы системы линейных уравнений.
- Вычислить алгебраические дополнения к минорам.
- Транспонировать полученную матрицу алгебраических дополнений.
- Разделить полученную матрицу на определитель.
2.3. Пример вычисления обратной матрицы
Для наглядности рассмотрим пример вычисления обратной матрицы.
Дана матрица системы уравнений:
| 2 | 3 |
| 4 | 5 |
Вычислим определитель этой матрицы, используя правило Саррюса:
| 2 | 3 | 2 |
| 4 | 5 | 4 |
Определитель равен (2 * 5) – (3 * 4) = -2. Так как определитель не равен нулю, обратная матрица существует.
Вычислим миноры матрицы, а затем алгебраические дополнения:
| 5 | -4 |
| -3 | 2 |
Транспонируем полученную матрицу:
| 5 | -3 |
| -4 | 2 |
Поделим полученную матрицу на определитель:
| -5/2 | 3/2 |
| 2 | -5 |
Таким образом, обратная матрица для данной системы уравнений равна:
| -5/2 | 3/2 |
| 2 | -5 |
Примеры решения систем линейных уравнений методом Крамера
Пример 1:
Рассмотрим следующую систему линейных уравнений:
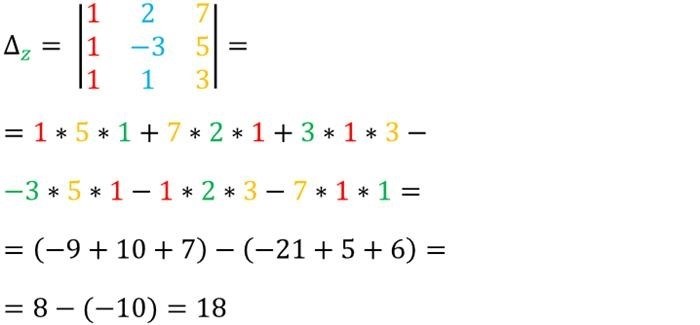
2x + 3y = 8
x – 2y = -5
Для начала найдем определитель основной системы:
|2 3|
|1 -2|
Определитель основной системы равен: (2 * -2) – (3 * 1) = -4 – 3 = -7
Теперь найдем определитель системы, в которой заменили столбец коэффициентов при x:
|8 3|
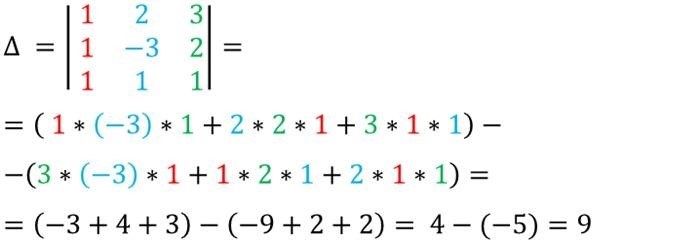
Определитель системы с новым столбцом равен: (8 * -2) – (3 * -5) = -16 + 15 = -1
И, наконец, определитель системы, в которой заменили столбец коэффициентов при y:
2 8
1 -5
Определитель системы с новым столбцом равен: (2 * -5) – (8 * 1) = -10 – 8 = -18
Теперь решим полученные уравнения методом Крамера:
x = -1 / -7 = 1/7 ≈ 0.143
y = -18 / -7 = 18/7 ≈ 2.571
Итого, решение системы линейных уравнений методом Крамера: x ≈ 0.143, y ≈ 2.571
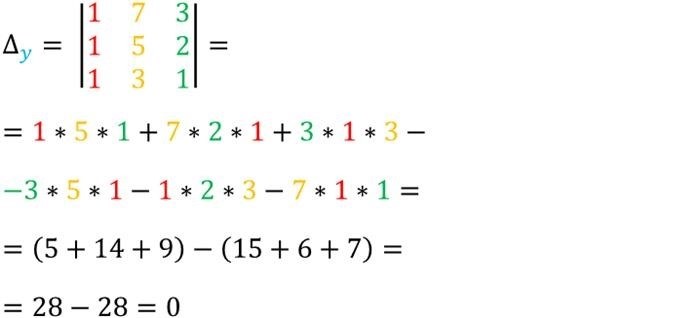
Пример 2:
Рассмотрим следующую систему линейных уравнений:
3x – 2y = 7
5x + 4y = -1
Найдем определитель основной системы:
|3 -2|
|5 4|
Определитель основной системы равен: (3 * 4) – (-2 * 5) = 12 + 10 = 22
Определитель системы с новым столбцом при x:
|7 -2|
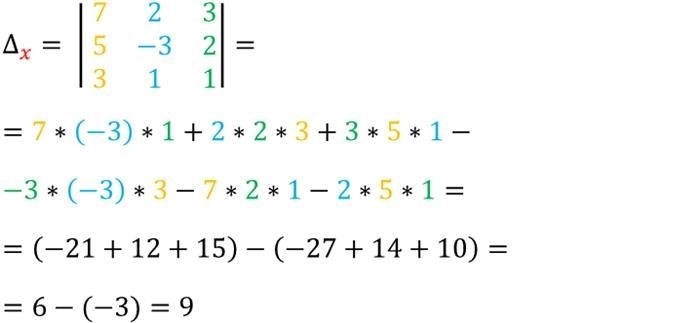
Определитель системы с новым столбцом равен: (7 * 4) – (-2 * -1) = 28 – 2 = 26
Определитель системы с новым столбцом при y:
3 7
5 -1
Определитель системы с новым столбцом равен: (3 * -1) – (7 * 5) = -3 – 35 = -38
Решим полученные уравнения методом Крамера:
x = 26 / 22 = 13/11 ≈ 1.182
y = -38 / 22 = -19/11 ≈ -1.727
Итого, решение системы линейных уравнений методом Крамера: x ≈ 1.182, y ≈ -1.727
К началу страницы
В данной статье мы рассмотрели основные принципы и шаги метода Крамера, а также привели примеры его применения. Метод Крамера является удобным инструментом для решения систем линейных уравнений с небольшим количеством неизвестных, но требует наличия определителей матриц и потенциально может быть затратным по вычислительным ресурсам при большом количестве переменных.
Если у вас возникнут вопросы или затруднения при использовании метода Крамера, рекомендуется обратиться к материалам литературы или обратиться к специалистам в области линейной алгебры. Надеемся, что данная статья помогла вам разобраться в этом методе и применить его на практике!
Итак, мы рассмотрели:
- Основные принципы метода Крамера;
- Шаги решения системы линейных уравнений методом Крамера;
- Примеры применения метода Крамера для решения систем уравнений.
Теперь вы знаете, как применять метод Крамера для решения систем линейных уравнений и можете использовать данный метод в своих будущих задачах. Удачи вам!