Решение показательных уравнений и неравенств

Показательные уравнения и неравенства являются основными понятиями в алгебре. Они играют важную роль в решении различных математических задач и имеют широкое применение в реальной жизни. В этой статье мы рассмотрим методы и приемы решения показательных уравнений и неравенств, а также покажем примеры их применения.

Показательные неравенства и методы их решения

• Метод замены переменной
• Метод приведения к общему основанию
• Метод графического представления

Метод замены переменной

Один из наиболее распространенных методов решения показательных неравенств – метод замены переменной. Этот метод базируется на замене сложного выражения в показателе степени на новую переменную, которую затем можно легко решить стандартными методами.

Например, рассмотрим неравенство вида:

5^2x-1 < 8^x+3

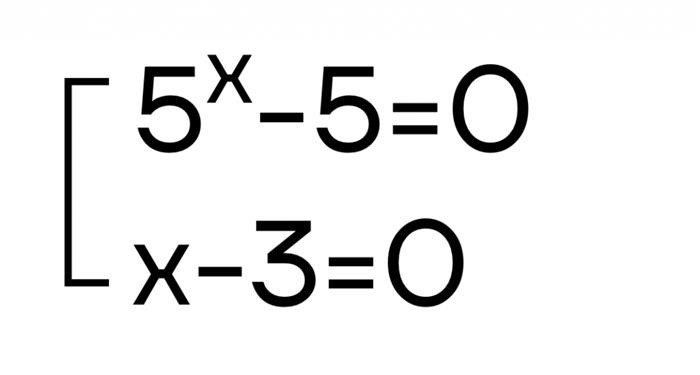
Заменим выражение в показателе степени на новую переменную:

let y = 2x-1

Получим новое уравнение:

5^y < 8^(y+4)/2

Теперь можно решить это уравнение, используя стандартные методы, а затем найти значения исходной переменной x.

Метод приведения к общему основанию

Еще одним способом решения показательных неравенств является метод приведения к общему основанию. Этот метод заключается в приведении всех показателей степени к одному и тому же основанию.

Например, рассмотрим неравенство вида:

2^x > 3^x-2

Приведем оба показателя степени к основанию 2:

(2¹)^x > (3¹)^x-2

Теперь можно сравнить только показатели степени и решить получившееся уравнение.

Метод графического представления

Метод графического представления основан на построении графиков функций, заданных показателями степени, и определении области значений, при которых неравенства выполняются. Этот метод может быть полезным при решении сложных показательных неравенств или для визуализации решений.

Повторение свойств степеней

Давайте вспомним основные свойства степеней:

1. Умножение степеней с одинаковыми основаниями

При умножении степеней с одинаковыми основаниями их показатели суммируются:

a^m * aⁿ = a^m+n

Например: 2³ * 2⁴ = 2⁷ = 128

2. Деление степеней с одинаковыми основаниями

При делении степеней с одинаковыми основаниями их показатели вычитаются:

a^m / aⁿ = a^m-n

Например: 5⁶ / 5³ = 5^6-3 = 5³ = 125

3. Возведение степени в степень

При возведении степени в степень показатели умножаются:

(a^m)ⁿ = a^m*n

Например: (3²)⁴ = 3^2*4 = 3⁸ = 6561

4. Умножение степени на число

При умножении степени на число, показатель остается неизменным:

(a * b)ⁿ = aⁿ * bⁿ

Например: (2 * 3)⁴ = 2⁴ * 3⁴ = 16 * 81 = 1296

5. Возведение в отрицательную степень

При возведении числа в отрицательную степень, число меняет знак, а затем возводится в положительную степень:

a^-n = 1 / aⁿ

Например: 2^-3 = 1 / 2³ = 1 / 8 = 0.125

Знание и применение этих свойств позволяет упрощать выражения, решать уравнения и неравенства, а также проводить различные алгебраические преобразования.

Показательная функция и её основные свойства

Показательные функции обладают несколькими основными свойствами, которые важно учитывать при работе с ними:

1. Интервалы определения

Показательная функция определена только для положительных значений показателя степени. Интервал определения такой функции является множеством положительных чисел: x > 0.

2. Монотонность

В зависимости от значения базы показательной функции a, она может быть как возрастающей, так и убывающей.

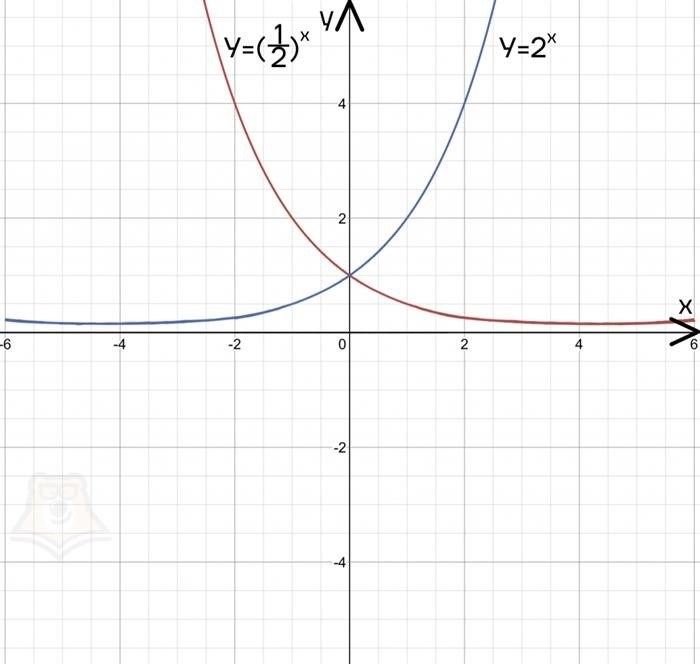
• При a > 1 показательная функция возрастает. Это значит, что с увеличением показателя степени x, значение функции y также возрастает.
• При 0 < a < 1 показательная функция убывает. В этом случае, с увеличением значения показателя степени x, значение функции y уменьшается.

3. Операции над показательными функциями

Показательные функции могут участвовать в различных операциях, таких как сложение, вычитание, умножение и деление. При этом выполняются следующие правила:

• При умножении показательных функций с одинаковой базой, показатели степени суммируются: a x * a y = a (x + y).
• При делении показательных функций с одинаковой базой, показатели степени вычитаются: a x / a y = a (x – y).
• При возведении показательной функции с несколькими слагаемыми в степень, показатель степени умножается на каждое слагаемое: (a x) y = a (x * y).

4. График показательной функции

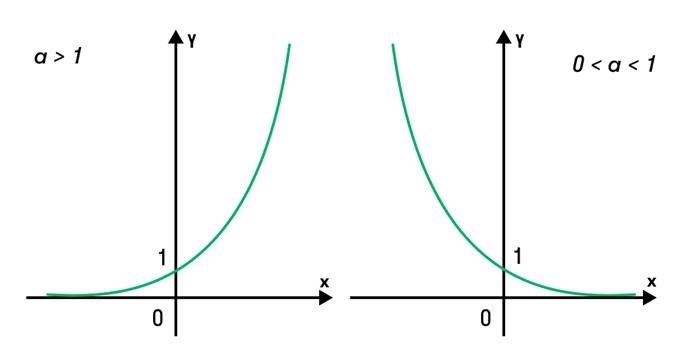
График показательной функции имеет определенные особенности в зависимости от значения базы a:

• При a > 1 график функции проходит через точку (0, 1) и возрастает, стремясь к положительной бесконечности.
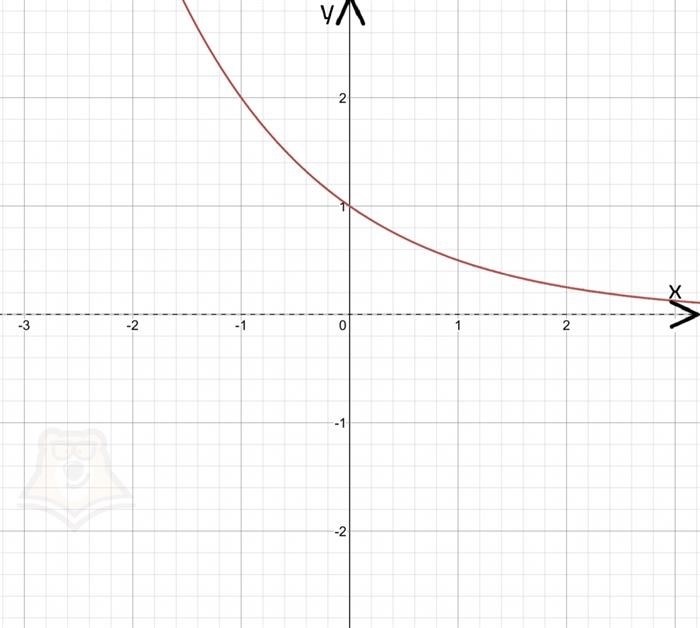
• При 0 < a < 1 график функции также проходит через точку (0, 1), но убывает, стремясь к 0.

Подписи к слайдам:

В данной статье были представлены основные принципы решения показательных уравнений и неравенств. Мы рассмотрели как решать уравнения с положительными и отрицательными показателями, а также уравнения с неестественными показателями. В процессе решения нам необходимо было применять различные свойства степеней и логарифмов для упрощения уравнений и нахождения точных решений.

Также мы изучили способы решения показательных неравенств. В частности, были рассмотрены неравенства с положительными и отрицательными показателями, а также неравенства с неограниченным и ограниченным интервалами. Нам пришлось применять некоторые трансформации и свойства показателей степени, чтобы получить точные интервальные решения.

Итак, мы затронули основные аспекты решения показательных уравнений и неравенств. Важно помнить, что каждое уравнение и неравенство требует индивидуального подхода и может иметь свои особенности и сложности. Чтобы научиться решать такие задачи в совершенстве, необходимо много практиковаться и изучать различные виды уравнений и неравенств.